Sbírka řešených úloh

Moment setrvačnosti cykloidy

Úloha číslo: 2087

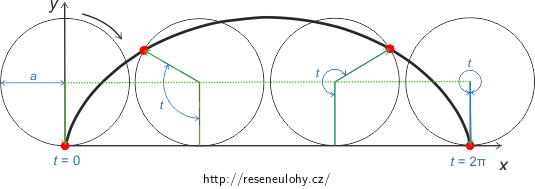
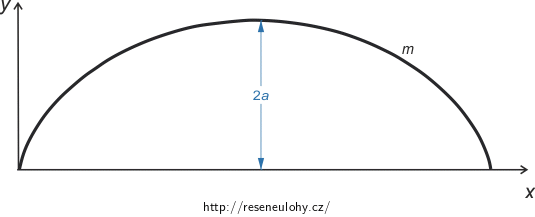
Určete moment setrvačnosti jednoho oblouku homogenní cykloidy vůči ose x. Zadánu máte výšku cykloidy v jejím nejvyšším bodě 2a a její celkovou hmotnost m.

• Rozbor

  Vzorec pro výpočet momentu setrvačnosti jednoho hmotného bodu je velmi jednoduchý, proto budeme vycházet právě z něj. Naše cykloida je sice spojité těleso, ne jen jeden bod, ale můžeme si ji velmi snadno představit jako soustavu mnoha hmotných bodů, které jsou velmi těsně vedle sebe. Celkově (můžeme říci jakoby „s odstupem“) tvoří tato řada bodů celou cykloidu. Z této analogie můžeme odvodit náš postup. Začneme vzorcem pro moment setrvačnosti jednoho hmotného bodu a uvědomíme si, že momenty setrvačnosti soustavy více bodů se budou jednoduše sčítat. Pokud si bodů představíme dostatek, uvědomíme si, že jejich poloha v prostoru se po cykloidě mění téměř spojitě. Pro součet momentů setrvačnosti takto „natěsnaných“ bodů bude možné použít integrální tvar, který si můžeme snadno odvodit.

  Do integrálního tvaru momentu setrvačnosti tělesa bude zapotřebí za veličiny dosadit vhodné výrazy, které nám popíší cykloidu po částech (abychom mohli sčítat jednotlivé malé části). Tyto vlastnosti se vyskytují u parametrických rovnic. Další nezbytnou částí pro řešení této úlohy budou tedy parametrické rovnice cykloidy. Tyto rovnice následně dosadíme do rovnice pro moment setrvačnosti, aby skutečně popisovaly právě náš objekt.

  Pokud budeme s integrálním tvarem momentu setrvačnosti pracovat dále, zjistíme, že obsahuje element hmotnosti, který ale neznáme. Při našem řešení však ukážeme způsob, jak ho lehce nahradit elementem délky. Pro další řešení budeme tedy muset znát také to, jak je dlouhý náš elementární kousek cykloidy, tedy vzorec pro délku elementu křivky. Nejprve obecně, poté konkrétně pro cykloidu.

  K celkovému řešení pak bude potřeba všechny tyto vzorce spojit vhodně dohromady a integrovat.

• Nápověda

  Pro úspěšné vyřešení této úlohy je zapotřebí znát tři body:

  a) vztah pro moment setrvačnosti hmotného bodu a z něj odvodit vztah pro libovolné tuhé těleso,

  b) parametrické rovnice cykloidy,

  c) vzorec pro délku malého úseku libovolné křivky ds.

• Řešení nápovědy a

  Moment setrvačnosti budeme značit písmenem J. Pro moment setrvačnosti jednoho hmotného bodu platí vzorec

  \[J=mr^2,\]

  kde m představuje hmotnost bodu a r jeho vzdálenost od osy otáčení.

  Máme-li soustavu n hmotných bodů, vypočítáme celkový moment setrvačnosti této soustavy jako součet momentů setrvačnosti jednotlivých bodů.

  \[J=\sum_{i=1}^n m_i r_i^2.\]

  Množství bodů je možné neomezeně zvyšovat, čímž se dostaneme ke vzorci pro moment setrvačnosti spojitého tuhého tělesa (jedná se vlastně o soustavu nekonečně mnoha malých hmotných bodů)

  \[J=\int r^2 \mathrm{d} m.\]

  Podrobněji je teorie výpočtu momentu setrvačnosti vysvětlena v úloze Moment setrvačnosti tyče.

• Řešení nápovědy b

  Cykloida je křivka, kterou opíše jeden z bodů kružnice, která se valí bez prokluzu po přímce. Tato křivka se nejčastěji vyjadřuje parametrickými rovnicemi, které mají tvar

  \[x=a (t-\sin t)\] \[y=a (1-\cos t).\]

  Písmeno a představuje v těchto rovnicích poloměr valící se kružnice, t je proměnný parametr (udává, o jaký úhel se kružnice při valení otočila; t nabývá hodnot od 0 do 2π a je v radiánech).

  

  Tyto rovnice jsou velmi podrobně odvozeny v úloze Délka oblouku cykloidy.

• Řešení nápovědy c

  Vzorec pro délku elementu libovolné křivky byl odvozen v úloze Délka oblouku cykloidy, v odstavci Řešení nápovědy b. V této úloze měl tvar

  \[ \Delta s= \sqrt{\left( \frac{\Delta x}{\Delta t} \right)^2+ \left( \frac{\Delta y}{\Delta t} \right)^2} \Delta t.\]

  Pozor: v této rovnici představuje písmeno t parametr, ne čas!

  Pro infinitezimální kousek křivky je možné vzorec jednoduše přepsat na

  \[ \mathrm{d} s= \sqrt{\left( \frac{\mathrm{d} x}{\mathrm{d} t} \right)^2+ \left( \frac{\mathrm{d} y}{\mathrm{d} t} \right)^2} \mathrm{d} t.\]

• Řešení

  Začneme vyjádřením momentu setrvačnosti tuhého spojitého tělesa

  \[J=\int r^2 \mathrm{d} m.\]

  V tomto vzorci by bylo zapotřebí integrovat přes malé kousky hmotnosti, což by bylo složité. Daleko jednodušší bude převést kousek hmotnosti na kousek objemu. Použijeme známý vzorec pro hmotnost v závislosti na objemu a hustotě ρ

  \[\mathrm{d}m=\rho \mathrm{d}V.\]

  Jelikož naše cykloida je v zásadě jednorozměrný útvar (má jen svou délku s), není třeba zabývat se žádnými dalšími rozměry a vzorec se dále zjednoduší. (Můžete si představit, že vyšetřujeme moment setrvačnosti velmi tenkého, ale dlouhého drátu ve tvaru cykloidy - tloušťka bude v porovnání s délkou jistě zanedbatelná.)

  \[\mathrm{d}m=\rho\ \mathrm{d}s.\]

  Náš vzorec pro moment setrvačnosti získá tvar

  \[ J\,=\,\int{\rho r^2}\mathrm{d}s. \]

  Pokud si navíc uvědomíme, že osa je v našem případě souhlasná se souřadnou osou x, můžeme vzdálenost každého elementu cykloidy od osy psát pouze jako její y-ovou souřadnici. Moment setrvačnosti bude nyní možné vyjádřit vzorcem

  \[J=\int_\Gamma \rho y^2\ \mathrm{d} s.\]

  Γ pod integrálem označuje, že budeme integrovat přes jeden oblouk cykloidy. ρ zde tedy představuje délkovou hustotu.

  Nyní je zapotřebí dosadit za y a ds. Nejprve dosadíme za ds, protože po jeho dosazení nám přibydou další y. Víme, že ds představuje element délky křivky (viz Nápověda/Řešení nápovědy c), můžeme tedy psát:

  \[ \mathrm{d} s= \sqrt{\left( \frac{\mathrm{d} x}{\mathrm{d} t} \right)^2+ \left( \frac{\mathrm{d} y}{\mathrm{d} t} \right)^2}\ \mathrm{d} t.\] A dosazením získáme \[J=\int_\Gamma \rho y^2 \sqrt{\left( \frac{\mathrm{d} x}{\mathrm{d} t} \right)^2+ \left( \frac{\mathrm{d} y}{\mathrm{d} t} \right)^2}\ \mathrm{d} t.\tag{1}\]

  Nyní je zapotřebí dosadit za y a x. Jelikož potřebujeme integrovat přes jeden celý oblouk, budou se y a x v rovnici měnit jako y-ová a x-ová souřadnice této křivky, můžeme tedy dosadit z parametrických rovnic samotné cykloidy

  \[x=a (t-\sin t)\] \[y=a (1-\cos t).\]

  V naší rovnici se však x a y vyskytují také v derivacích. Pokud si nejste jisti, doporučuji nejprve si parametrické rovnice roznásobit.

  \[x=at-a\sin t\] \[y=a-a\cos t\] \[\frac{\mathrm{d}x}{\mathrm{d}t}=a-a\cos t\] \[\frac{\mathrm{d}y}{\mathrm{d}t}=0+a\sin t.\]

  Pokud tyto výsledky dosadíme do rovnice (1), dostaneme:

  \[J=\int_\Gamma \rho a^2 (1-\cos t)^2 \sqrt{(a-a\cos t)^2 + a^2 \sin^2 t}\ \mathrm{d}t.\]

  Křivka Γ, tedy jeden oblouk naší cykloidy, je dána parametricky a parametr je zároveň to, podle čeho integrujeme. Jako integrační meze tedy určitě zvolíme krajní meze parametru t, které jsou pro jeden oblouk cykloidy 0 a 2π.

  Současně provedeme drobnou úpravu v prvním členu pod odmocninou, kde můžeme vytknout a.

  \[J=\int_0^{2\pi} \rho a^2 (1-\cos t)^2 \sqrt{a^2(1-\cos t)^2 + a^2 \sin^2 t}\ \mathrm{d}t.\]

  A nyní je zapotřebí „jen“ spočítat určitý integrál vhodnými úpravami a v jistém bodě i substitucí. Podrobný postup pro výpočet tohoto integrálu je uveden v sekci „Výpočet integrálu“ na konci tohoto řešení. My budeme dále pokračovat rovnou s výsledkem:

  \[J=\frac{32}{15}(2a)^3 \rho. \]

  Hustotu cykloidy jsme sice neměli zadánu, ale v této fázi nebude problém ji nahradit zpětně za hmotnost. Pro objemovou hustotu hmotnosti homogenního tělesa bychom psali

  \[ \rho =\frac {m}{V},\]

  kde V je objem tělesa, jehož hustotu počítáme. My jsme ale v úvodu tohoto řešení podotkli, že u cykloidy není zapotřebí uvažovat všechny rozměry, ale jen její délku s.

  \[\rho\,=\,\frac{m}{s}\]

  Délku cykloidy je možné vypočítat a vychází jako osminásobek poloměru kružnice, která cykloidu vytvořila (Viz Délka oblouku cykloidy)

  \[\rho=\frac{m}{8a}.\]

  Zbývá už pouze dosadit a následný vztah zjednodušit

  \[J=\frac{32}{15} 2^3 a^3 \frac{m}{8a}.\]

  A výsledný moment setrvačnosti jednoho oblouku homogenní cykloidy vůči ose x je

  \[J=\frac{32}{15}a^2m.\]

• Výpočet integrálu

  Integrál, který musíme spočítat, je

  \[J=\int_0^{2\pi} \rho a^2 (1−\cos t)^2 \sqrt{a^2(1−\cos t)^2 + a^2 \sin^2 t}\ \mathrm{d}t\]

  V první úpravě vytkneme před integrál konstantu – hustotu. Zároveň vidíme, že pod odmocninou se v obou členech nachází a² a je tedy možné jej vytknout přímo před odmocninu jako a.

  \[J=\rho \int_0^{2\pi} a^3 (1−\cos t)^2 \sqrt{(1−\cos t)^2 + \sin^2 t}\ \mathrm{d}t\]

  Dále budeme upravovat výraz pod odmocninou. První člen je možné si rozepsat a tím dostaneme „goniometrickou jedničku“.

  \[J=\rho \int_0^{2\pi} a^3 (1−\cos t)^2 \sqrt{1−2\cos t +\cos^2 t + \sin^2 t}\ \mathrm{d}t\] \[J=\rho \int_0^{2\pi} a^3 (1−\cos t)^2 \sqrt{2−2\cos t}\ \mathrm{d}t\]

  Protože a je také konstanta, je možné ji vytknout před integrál. Rovnou si vytkneme i odmocninu ze dvou, abychom pod odmocninou dostali podobný výraz jako v závorce.

  \[J=a^3 \rho \int_0^{2\pi} (1−\cos t)^2 \sqrt{2} \sqrt{1−\cos t}\ \mathrm{d}t\]

  V tomto tvaru je možné oba výrazy s 1−cos t sloučit a sečíst jejich exponenty.

  \[J=a^3 \rho \int_0^{2\pi} \sqrt{2} (1−\cos t)^\frac{5}{2}\ \mathrm{d}t = a^3 \rho \int_0^{2\pi} \sqrt{2} (\sqrt{1−\cos t})^5\ \mathrm{d}t\]

  Stále nejsme ve tvaru, který bychom dokázali integrovat, pokusíme se tedy výraz upravit tak, abyhcom mohli použít nějaký známý goniometrický vzorec. Výraz pod 5. mocninou má velmi blízko ke vzorci

  \[|\sin {\frac {t}{2}}|=\sqrt{\frac{1−\cos t}{2}},\]

  a proto jej na tento tvar upravíme. Abychom mohli člen 1−cos t vydělit dvojkou, musíme dvojku dostat pod odmocninu i pod pátou mocninu tak, abychom nezměnili význam rovnice. Rovnici tedy musíme nejenom vydělit, ale i vynásobit následujícím způsobem:

  \[J=a^3 \rho \int_0^{2\pi} \sqrt{2} (\sqrt{1−\cos t})^5\ \mathrm{d}t \cdot \frac{(\sqrt 2)^5}{(\sqrt 2)^5}\] \[J=a^3 \rho \int_0^{2\pi} 2^3 \left( \sqrt{\frac{1−\cos t}{2}}\right)^5\ \mathrm{d}t \] \[J=a^3 \rho \int_0^{2\pi} 2^3 |\sin\frac{t}{2}|^5 \mathrm{d}t \]

  Absolutní hodnota by nám mohla zdánlivě vadit, ale můžeme ji jednoduše vynechat. Sinus bude v našem integrálu nabývat pouze hodnot od 0 do 1 (integrační meze jsou od 0 do 2π a v sinu jsou děleny 2) a na tomto intervalu je sinus pouze kladný nebo nula.

  \[J=(2a)^3 \rho \int_0^{2\pi} (\sin\frac{t}{2})^5 \mathrm{d}t \]

  Na tento itegrál již bude zapotřebí použít první substituci. Při této příležitosti také přepočítáme integrační meze.

  \[u=\frac{t}{2}\] \[\mathrm{d}u=\frac{1}{2} \mathrm{d}t\] \[2\mathrm{d}u=\mathrm{d}t\] \[J=(2a)^3 \rho \int_0^{\pi} 2(\sin u)^5 du\]

  Bohužel i tento integrál bude zapotřebí dále upravovat a to úpravou výrazů, goniometrickými vztahy a další substitucí.

  Vytkneme dvojku z integrálu.

  \[J=(2a)^3 2\rho \int_0^{\pi} (\sin^2 u)^2\ \sin u\ du\]

  Za mocninu sinu dosadíme z goniometrické jedničky

  \[J=(2a)^3 2\rho \int_0^{\pi} (1−\cos^2 u)^2\ \sin u\ du.\]

  Umocníme výraz v závorce na druhou

  \[J=(2a)^3 2\rho \int_0^{\pi} (1−2\cos^2 u + \cos^4 u)\ \sin u\ du.\]

  A provedeme další substituci. V závorce máme vícekrát kosinus, ale za závorkou pouze jediný sinus, dokážeme tedy udělat substituci tak, abychom sinus odstranili.

  \[v=\cos u\] \[\mathrm{d}v=−\sin u\ \mathrm{d}u\] \[J=(2a)^3 2\rho \int_1^{−1} [−(1−2v^2+v^4)] dv\]

  A konečně takovýto tvar už dokážeme integrovat. Jednoduše budeme integrovat jeden sčítanec po druhém.

  \[J=(2a)^3 2\rho [−v+\frac{2}{3}v^3−\frac{1}{5}v^5]_1^{−1}\]

  Zbývá už pouze dosadit a zjednodušit. Výsledek je

  \[J=\frac{32}{15} 2^3 a^3 \frac{m}{8a}\]

• Odpověď

  Výsledný moment setrvačnosti jednoho oblouku homogenní cykloidy vzhledem k ose x je

  \[J=\frac{32}{15}a^2m.\]

• Podobné úlohy

  Máte-li problém s odvozením parametrických rovnic cykloidy, nebo s výpočtem její délky, doporučuji pročíst si úlohu Délka oblouku cykloidy, kde je obojí velmi podrobně vysvětleno.

  Potřebujete-li si procvičit výpočet momentu setrvačnosti, vyzkoušejte si úlohy Moment setrvačnosti tyče, Moment setrvačnosti dvou kuliček a Moment setrvačnosti válce.