Tlumené kmity

Úloha číslo: 530

Kondenzátor o kapacitě 10 nF je vyplněn dielektrikem se ztrátovým úhlem δ, pro něž platí tg δ = 0,01. Kondenzátor nabijeme na napětí 100 V a pak připojíme k ideální cívce s indukčností 400 μH. V obvodu vzniknou tlumené harmonické kmity. Za jak dlouho poklesne amplituda kmitů na 1 V?

Pozn.: Ztrátový úhel δ je fázový posun mezi proudem tekoucím skutečným a ideálním kondenzátorem.

Nápověda – ztrátový úhel
Ztrátový úhel δ je úhel, o který se liší fázový posun mezi průběhem okamžitého napětí a proudu na reálném kondenzátoru od fázového posunu na ideálním kondenzátoru, který je −π/2.
Nápověda – sestavení diferenciální rovnice
Musíme získat rovnici pro časový průběh napětí. Jelikož se jedná o paralelní zapojení, je napětí na všech prvcích v obvodu stejné, tedy ve výsledné rovnici budeme mít pouze jednu neznámou.

Pomocí 1. Kirchhoffova zákona sestavíme rovnici pro okamžité hodnoty proudů na prvcích v obvodu. Do rovnice za jednotlivé proudy dosadíme výrazy, ve kterých figuruje okamžitá hodnota napětí, tím získáme hledanou diferenciální rovnici pro průběh napětí v obvodu.
Rozbor
Nahradíme ztrátový kondenzátor paralelním zapojením ideálního kondenzátoru a rezistoru. Použijeme 1. Kirchhoffův zákon a sestavíme diferenciální rovnici pro časový průběh napětí v obvodu. Rovnici vyřešíme a rozebereme její výsledný tvar, ze kterého určíme pokles amplitudy kmitů.

Zápis

U₀ = 100 V	počáteční napětí, na které je kondenzátor nabit
tg δ = 0,01	vztah pro ztrátový úhel kondenzátoru
C = 10 nF	kapacita kondenzátoru
L = 400 μH	indukčnost cívky
U = 1 V	hodnota, na kterou má amplituda napětí klesnout
t_x = ? (s)	čas, za který dojde k požadovanému poklesu napětí U

Řešení – nahrazení ztrátového kondenzátoru
Ztrátový kondenzátor nahradíme paralelní kombinací ideálního kondenzátoru a rezistoru:

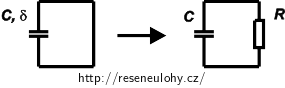
Ze zadání víme, že pro ztrátový úhel δ platí
\[ \mathrm{tg}\,\delta = 0{,}01.\]
Nakreslíme si fázorový diagram, ve kterém nahradíme ztrátový kondenzátor paralelním zapojením ideálního kondenzátoru a rezistoru a vyznačíme ztrátový úhel:

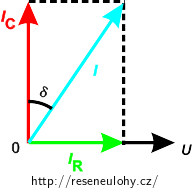
Pozn.: Velikosti fázorů na obrázku nejsou kvůli přehlednosti zakresleny v poměru.

Z fázorového diagramu vidíme, že platí
\[ \mathrm{tg}\, \delta = \frac {I_\mathrm{R}}{I_\mathrm{C}}. \]
Upravíme tak, aby ve vztahu vystupoval odpor rezistoru:
\[ \mathrm{tg}\, \delta = \frac {I_\mathrm{R}}{I_\mathrm{C}}= \frac{\frac{U}{ R}}{\frac{U}{X_\mathrm{C}}} = \frac {X_\mathrm{C}}{R}=\frac{\frac{1}{\omega C}}{R} = \frac{1}{\omega R C} \]
a vyjádříme odpor rezistoru:
\[ R = \frac{1}{ \omega C \mathrm{tg} \, \delta} .\]
Vidíme, že pro výpočet velikosti odporu rezistoru potřebujeme znát frekvenci kmitů ω. Protože tlumení kondenzátoru δ je malé, můžeme za frekvenci ω vzít frekvenci vlastních kmitů ω₀:
\[ \omega = \omega_0.\]
Tedy chceme frekvenci s největší amplitudou kmitů, kterou získáme ze vztahu
\[ {\omega}_0 = \frac{1}{\sqrt{LC}} \]
a dosadíme do vztahu pro výpočet velikosti odporu rezistoru:
\[ R = \frac{1}{{\omega}_0 C \mathrm{tg} \, \delta} = \frac{1}{\frac{ C \mathrm{tg} \, \delta}{\sqrt{LC}}}= \frac{\sqrt{LC}}{C \mathrm{tg} \, \delta}. \]

Dosadíme číselné hodnoty a vypočteme:
\[ R= \frac{\sqrt{LC}}{ C \mathrm{tg} \, \delta} = \frac{\sqrt{400{\cdot} 10^{-6} \cdot 10^{-8}}}{ 10^{-8} \cdot 0{,}01 }= 20\,\mathrm k\Omega \]
Řešení – tlumené kmitání
Abychom mohli určit pokles amplitudy napětí na určitou hodnotu, musíme nejprve získat rovnici pro časový průběh napětí.

Připojíme-li na nabitý ztrátový kondenzátor ideální cívku, teče proud z ideálního kondenzátoru do rezistoru a cívky a zpět.

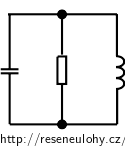
Matematicky si to popíšeme pomocí 1. Kirchhoffova zákona:
\[ i_\mathrm{C} = i_\mathrm{R} + i_\mathrm{L}, \]
kde i_C je okamžitá hodnota proudu na kondenzátoru, i_R okamžitá hodnota proudu na rezistoru a i_L okamžitá hodnota proudu na cívce.

Pozn.: Protože jsou tyto proudy vůči sobě fázově posunuty, platí 1. Kirchhoffův zákon pro okamžité hodnoty proudu, nikoli pro jejich amplitudy.

Protože jsou všechny prvky zapojeny paralelně, je na nich stejné okamžité napětí u.

Napišme si vztahy mezi okamžitým proudem i a napětím u na všech třech prvcích:

ideální kondenzátor:
\[ i_\mathrm{C} = - \frac{ \mathrm{d}Q}{\mathrm{d}t} = -C\frac {\mathrm{d}u}{\mathrm{d}t}, \]
rezistor:
\[ i_\mathrm{R} = \frac{u}{R}, \]
cívka:
\[ u = L \frac{\mathrm{d} i_\mathrm{L}}{\mathrm{d}t} \Rightarrow i_\mathrm{L} = \frac{1}{L} \int_0^\mathrm{t} u \mathrm{d}t .\]
Vztahy pro okamžité proudy dosadíme do 1. Kirchhoffova zákona:
\[ i_\mathrm{C} = i_\mathrm{R} + i_\mathrm{L} \] \[ -C\frac {\mathrm{d}u}{\mathrm{d}t} = \frac{u}{R} + \frac{1}{L} \int_0^\mathrm{t} u \mathrm{d}t.\]
Rovnici upravíme:
\[ C\frac {\mathrm{d}u}{\mathrm{d}t} + \frac{u}{R} + \frac{1}{L} \int_0^\mathrm{t} u \mathrm{d}t = 0\] \[ \frac {\mathrm{d}u}{\mathrm{d}t} + \frac{u}{R C} + \frac{1}{L C} \int_0^\mathrm{t} u \mathrm{d}t = 0\]
a zderivujeme podle času:
\[ \frac {\mathrm{d^2}u}{\mathrm{d}t^2} + \frac{1}{RC} \frac{\mathrm{d}u}{\mathrm{d}t} + \frac{1}{LC} u = 0.\]
Tím jsme získali homogenní lineární diferenciální rovnici s konstantními koeficienty pro časový průběh napětí v obvodu u. Tuto rovnici budeme řešit v dalším oddíle.
Řešení – diferenciální rovnice pro časový průběh napětí
V předchozím oddíle jsme odvodili následující rovnici:
\[ \frac {\mathrm{d^2}u}{\mathrm{d}t^2} + \frac{1}{RC} \frac{\mathrm{d}u}{\mathrm{d}t} + \frac{1}{LC} u = 0.\]
Pro přehlednost budeme derivaci znázorňovat čárkou:
\[ u^{,,} + \frac{1}{RC} u^, + \frac{1}{LC}u = 0. \]
Jedná se o homogenní lineární diferenciální rovnici s konstantními koeficienty. Její řešení má tvar
\[ u = \mathrm{e}^{ \lambda t}, \]
kde λ je konstanta, kterou je třeba nalézt.

Spočítáme si potřebné derivace:
\[ u^, = \lambda \mathrm{e}^{ \lambda t},\ u^{,,}= {\lambda}^2 \mathrm{e}^{ \lambda t}\]
a dosadíme do diferenciální rovnice:
\[ {\lambda}^2 \mathrm{e}^{ \lambda t} + \frac{\lambda}{RC} \mathrm{e}^{ \lambda t} + \frac{1}{LC} \mathrm{e}^{ \lambda t}= 0. \]
Vydělíme nenulovým výrazem e^λt
\[ {\lambda}^2 + \frac{\lambda}{RC} + \frac{1}{LC} = 0. \]
Získali jsme tak kvadratickou rovnici pro hledanou konstantu λ, kterou budeme řešit. Nejprve spočítáme diskriminant:
\[ \mathrm{D} = \frac{1}{R^2 C^2} - 4 \frac{1}{LC}. \]
Dosadíme-li do diskriminantu zadané hodnoty (Pozn.: Všechny veličiny budeme dosazovat v základních či odvozených jednotkách.)
\[ \mathrm{D} = (\frac{1}{(20{\cdot} 10^3)^2\cdot (10{\cdot} 10^{-9})^2} - 4\cdot \frac{1}{400{\cdot} 10^{-6}\cdot 10{\cdot} 10^{-9} } )\] \[ \mathrm{D} = (25{\cdot} 10^8 - 25 {\cdot} 10^10)\mathrm\,\frac{1}{s^2} \dot= -2{,}5 {\cdot} 10^{11},\]
zjistíme, že vychází záporný, a tudíž λ bude komplexní s hodnotami:
\[ {\lambda}_{1, 2} = - \frac{1}{2RC} \pm \mathrm{j} \sqrt { \frac{1}{2R^2 C^2} - \frac{1}{L C}}, \]
kde \(\mathrm j \) označuje komplexní jednotku.

Označíme si:
\[ A = \frac{1}{2RC}, \] \[ B = \sqrt { \frac{1}{2R^2 C^2} - \frac{1}{L C}}, \]
to znamená, že:
\[ \lambda_{1{,}2}=A \pm \mathrm{j} B.\]
Řešení diferenciální rovnice má tvar lineární kombinace obou nalezených řešení:
\[u = K_1 \mathrm{e}^\mathrm{(-A +\mathrm{j}B)t} + K_2 \mathrm{e}^\mathrm{(-A -\mathrm{j}B)t},\]
což lze přepsat na
\[u = K \mathrm{e}^\mathrm{-At}\cos(\omega t + \varphi_0),\]
kde K₁, K₂, resp. K, φ₀ jsou konstanty, které jsou dány počátečními podmínkami.

Rozebereme si výsledný tvar rovnice pro okamžitou hodnotu napětí u:

tlumení amplitudy napětí v obvodu vyjadřuje \[ K \mathrm{e}^\mathrm{-At},\]

průběh okamžitých hodnot střídavého napětí určuje \( \cos(\omega t + \varphi_0).\)

Pro určení průběhu amplitudy tlumených kmitů musíme určit velikost konstanty K. Víme, že na začátku, tedy v čase t = 0 s, je napětí u v obvodu rovno amplitudě napětí U₀ = 100 V, tedy lze psát:
\[U_0 = K \mathrm{e}^\mathrm{-A\cdot 0},\] \[U_0 = K .\]
Pro průběh amplitudy tlumených kmitů U tedy dostáváme vztah
\[U = U_0 \mathrm{e}^\mathrm{-At}=U_0 \mathrm{e}^\mathrm{-\frac{t}{2RC}}.\]
Řešení – Amplituda tlumených kmitů
Změna amplitudy tlumených kmitů je popsána vztahem
\[U=U_0 \mathrm{e}^\mathrm{-\frac{t}{2RC}}.\]
Chceme určit čas t_x, za který amplituda poklesne na hodnotu U = 1 V. Řešíme tedy rovnici ve tvaru
\[ U =U_0 \mathrm{e}^\mathrm{-\frac{t_x}{2RC}} \] \[ \frac{U}{U_0} = e^\mathrm{-\frac{t_x}{2RC}}.\]
Rovnici zlogaritmujeme:
\[ \ln{\frac{U}{U_0}} =\ln{ e^\mathrm{-\frac{t_x}{2RC}}} \] \[ \ln{\frac{U}{U_0}} =-\frac{t_x}{2RC} \]
a vyjádříme hledaný čas t_x:
\[ t_\mathrm{x} = -2RC \ln{\frac{U}{U_0}}= 2RC \ln{{\frac{U_0}{U}}}.\]
Dosadíme číselně:
\[ t_\mathrm{x} =2RC \ln{\frac{U_0}{U}}= 2{\cdot} 20 \cdot 10^3 {\cdot} 10^{-8} \cdot \ln{{\frac{100}{1}}}\,\mathrm s \,\dot= \,1{,}8 {\cdot} 10^{-3} \,\mathrm s.\]
Odpověď
Amplituda kmitů poklesne na 1 V za 1,8·10^-3 s.