Sbírka řešených úloh

Nejpravděpodobnější, střední a střední kvadratická rychlost molekul plynu

Úloha číslo: 414

• Nápověda – Maxwellovo rozdělení

  Maxwellovo rozdělení, nebo také Maxwellovo-Boltzmannovo rozdělení popisuje systém klasických rozlišitelných částic, tedy např. molekul. Rozdělovací funkce pro velikost rychlosti molekul má tvar

  \[\rho \left( v\right) = 4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}}v^{2}e^{-\frac{mv^{2}}{2kT}}.\]

• Rozbor

  Nejpravděpodobnější rychlost molekul plynu řídících se Maxwellovým rozdělením je taková rychlost, při které nabývá graf rozdělení rychlostí svého maxima. Pokud tedy známe předpis tohoto rozdělení, stačí ho pouze zderivovat a tuto derivaci položit rovnu nule. Rychlost, pro kterou je derivace nulová, je ta nejpravděpodobnější.

  Střední rychlost molekul je průměrem všech velikostí rychlostí, kterými se molekuly daného plynu pohybují.

  Střední kvadratická rychlost molekul je taková rychlost, kterou kdyby se pohybovaly všechny molekuly, tak by měl plyn stejnou celkovou kinetickou energii, jako při skutečných rychlostech.

  Střední rychlost molekul spočítáme jako integrál z Maxwellova rozdělení vynásobeného rychlostí molekuly v. Integrovat budeme přes všechny možné rychlosti molekul, tedy od nuly do nekonečna.

  Střední kvadratickou rychlost spočítáme podobně, pouze Maxwellovo rozdělení vynásobíme v².

• Řešení

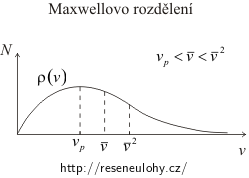
  Na následujícím obrázku je znázorněno Maxwellovo rozdělení velikosti rychlostí molekul plynu.

  Je zde vyznačena nejpravděpodobnější rychlost v_p, střední rychlost  a střední kvadratická rychlost \(\bar{v}^{2}\).

   

  

  Nejpravděpodobnější rychlost odpovídá maximu rozdělovací funkce (viz obrázek). Napíšeme si tuto rozdělovací funkci

  \[\rho \left( v\right) = 4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}}\,v^{2}\,e^{-\frac{mv^{2}}{2kT}},\]

  kde m je hmotnost jedné molekuly, k Boltzmannova konstanta a T termodynamická teplota.

  Rozdělovací funkci zderivujeme podle velikosti rychlosti v a získanou derivaci položíme rovnu nule (jde o obecný postup pro hledání extrémů funkcí).

  Dostáváme:

  \[\frac{\mathrm{d}\rho \left( v\right) }{\mathrm{d}v} = 4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}} \left( 2v\,e^{-\frac{mv^{2}}{2kT}} + v^{2}\,\left( -\frac{mv}{kT}\right) e^{-\frac{mv^{2}}{2kT}}\right) =\] \[=4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}}e^{-\frac{mv^{2}}{2kT}}\ v\ \left( 2 - \frac{m}{kT}v^{2}\right) = 0\]

  Při derivování jsme užili pravidla pro derivaci součinu a složené funkce. Dále využijeme toho, že vytknuté konstanty ani hodnota exponenciální funkce se nikdy nule nerovnají. Tak dostáváme dvě možná řešení

  \[ v = 0\qquad \mathrm{nebo} \qquad 2-\frac{m}{kT}v^{2} = 0.\]

  První možnost, tj. nulová rychlost odpovídá minimum v rozdělení rychlostí. Ze druhé možnosti dostáváme:

  \[v^{2} = \frac{2kT}{m},\] \[v = \sqrt{\frac{2kT}{m}}.\]

  Při další úpravě využijeme vztahy pro univerzální plynovou konstantu R = kN_A (kde N_A označuje Avogadrovu konstantu) a molární hmotnost plynu M_m = mN_A. Dostaneme

  \[v_{p} = \sqrt{\frac{2kT}{m}} = \sqrt{\frac{2RT}{M_{m}}}.\]

   

  Dále spočítáme střední rychlost molekul plynu. Pro tuto rychlost platí

  \[\bar{v} = \int_0^{\infty}{v \rho(v)}\,\mathrm{d}v = \int_0^{\infty}{4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}}v^{3}e^{-\frac{mv^{2}}{2kT}}}\,\mathrm{d}v.\]

  Pro přehlednější výpočet zavedeme následující označení:

  \[a = 4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}}\] \[b = \frac{m}{2kT}\]

  Dostáváme tedy výraz:

  \[\bar{v} = a\int_0^{\infty}{v^{3}e^{-bv^{2}}}\,\mathrm{d}v\]

  Nyní použijeme substituci s = v², ds = 2vdv a dostaneme:

  \[\bar{v} = \frac{a}{2}\int_0^{\infty}{se^{-bs}}\,\mathrm{d}s\]

  Dále použijeme metodu per partes (derivovat budeme s a integrovat e^−bs. Dostaneme:

  \[\bar{v} = \frac{a}{2}\cdot \left( \left[ -s\frac{1}{b}e^{-bs}\right] _{0}^{\infty} - \int_0^{\infty}{-\frac{1}{b}e^{-bs}}\,\mathrm{d}s \right) = \frac{a}{2}\,\left( 0+\frac{1}{b}\int_0^{\infty}{e^{-bs}}\,\mathrm{d}s\right) =\] \[=\frac{a}{2b}\left[-\frac{1}{b}e^{-bs}\right] _{0}^{\infty} = \frac{a}{2b^{2}} \]

  a po dosazení za konstanty a a b získáme:

  \[\bar{v} = \frac{4\pi}{2}\sqrt{\left( \frac{m}{2\pi kT}\right) ^{3}}\cdot \frac{4k^{2}T^{2}}{m^{2}} = \sqrt{\frac{8kT}{\pi m}} =\sqrt{\frac{8RT}{\pi M_{m}}}.\]

   

  Nyní spočítáme střední kvadratickou rychlost. K jejímu výpočtu budeme potřebovat následující vzorec, který lze najít ve vysokoškolských tabulkách.

  \[\int_{0}^{\infty}{x^{2n}e^{-\frac{x^{2}}{a^{2}}}}\, \mathrm{d}x = \sqrt{\pi}\,\frac{\left( 2n\right) !}{n!}\,\left( \frac{a}{2}\right) ^{2n+1}\]

  Pro střední kvadratickou rychlost platí:

  \[\bar{v}_{k}^{2} = \int_{0}^{\infty}{v^{2}\rho\left( v\right) }\, \mathrm{d}v = 4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}} \int_0^{\infty}{v^{4}e^{-\frac{mv^{2}}{2kT}}}\,\mathrm{d}v = \] \[=4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}}\ \sqrt{\pi}\,\frac{4!}{2!}\,\left( \frac{\sqrt{\frac{2kT}{m}}}{2}\right) ^{5} = \frac{3}{2}\sqrt{\left( \frac{m}{2\pi kT}\right) ^{3}\pi ^{3}\left( \frac{2kT}{m}\right) ^{5}}=\] \[=\frac{3kT}{m} = \frac{3RT}{M_{m}}\]

  Střední kvadratická rychlost pak je

  \[\bar{v}_{k} = \sqrt{\frac{3RT}{M_{m}}}.\]

• Odpověď

  Velikost nejpravděpodobnější rychlosti molekul v plynu, řídících se Maxwellovým rozdělením, je dána vztahem

  \[v_{p} = \sqrt{\frac{2kT}{m}} = \sqrt{\frac{2RT}{M_{m}}}.\]

  Pro velikost střední rychlosti platí \[\bar{v} = \sqrt{\frac{8RT}{\pi M_{m}}}\] a pro velikost střední kvadratické rychlosti platí \[\bar{v}_{k} = \sqrt{\frac{3RT}{M_{m}}}\,.\]