Radioaktivita

Úloha číslo: 996

Radioaktivní izotopy se rozpadají podle rovnice:

\[ \frac{\mathrm{d}x}{\mathrm{d}t}= -r x, \]

kde r se nazývá přeměnová konstanta daného izotopu, x je hmotnost v gramech, t je čas ve dnech.

Pro izotop thoria ²³⁴Th je r = 0,02828.

a) Vyřešte diferenciální rovnici pro daný izotop thoria, když víte, že v čase t = 0 byla hmotnost thoria 100 g.

b) Spočtěte, kolik gramů thoria se z původních 100 g rozpadne během 67 dnů.

c) Zjistěte, po kolika dnech zůstane ze 100 g thoria nerozpadlých 50 g.

d) Úlohu řešte pro několik různých hmotnosti (menších nebo rovných 100 g) dosud nerozpadlého thoria. Vyneste do grafu časovou závislost hmotnosti thoria a přesvědčte se, že je exponenciální.

Poznámka: Uvedená rovnice je jen pro číselné hodnoty, bez fyzikální jednotky.

Nápověda 1 ( k úloze a) )
Daná diferenciální rovnice je typu:
\[ \frac{\mathrm{d}y}{\mathrm{d}t} = f (y). \]
Zkuste si rozmyslet, jak daný typ rovnice řešíme.
Řešení nápovědy 1
Rovnice pro izotop thoria (²³⁴Th) vypadá následovně:
\[ \frac{\mathrm{d}x}{\mathrm{d}t}= -0{,}02828 x. \]
Provedeme integraci
\[ \frac {\mathrm{d}x}{x} = - 0{,}02828 \mathrm{d}t \] \[ \int\frac{\mathrm{d}x}{x} = -0{,}02828 \int \mathrm{d}t \] \[ \ln (\frac{x}{x_0}) = - 0{,}02828 t \]
Poznámka:V argumentu logaritmu jsme hmotnost x formálně vydělili konstantou x₀, která má rozměr hmotnosti, aby se v argumentu přirozeného logaritmu vyskytovala bezrozměrná veličina.

Aplikací exponenciály
\[ \frac{x}{x_0} = e^{-0{,}02828t}, \]
dostáváme výsledek
\[ x = x_0 e^{-0{,}02828t}. \]
Teď nezbývá nic jiného než určit konstantu x₀.

Víme, že v čase t = 0 bylo nerozpadlých 100 g thoria. Platí tedy
\[ 100 = x_0 e^{0}\hspace{20px} \Rightarrow \hspace{20px }x_0 = 100. \]
Výsledná závislost vypadá následovně:
\[ x (t) = 100 e^{-0{,}02828t}, \]
kde x je hmotnost v gramech, t je čas ve dnech.
Nápověda 2 ( k úloze b) )
Úkolem je zjistit, kolik gramů thoria se rozpadne během 67 dnů. Po dosazení za čas t = 67 získáte rovnici s jednou neznámou, kterou jednoduše vyřešíte.
Řešení nápovědy 2
Naší úlohou je zjistit, kolik gramů thoria se rozpadne během 67 dnů.

Proto do rovnice
\[ x = 100 e^{-0{,}02828t} \]
za čas dosadíme t = 67:
\[ x (67) = 100 e^{-0{,}02828\cdot{67}} \]
Dostáváme přibližný výsledek:
\[ x = 15 \hspace{2px} \mathrm{g}. \]
Víme tedy, že ze 100 g thoria zůstalo nerozpadlých 15 g.

Během 67 dnů se rozpadne 85 g thoria.
Nápověda 3 ( k úloze c) )
Úlohou je určit, za jaký čas zůstane ze 100 g thoria nerozpadlých 50 g.

Zkuste do vypočtené rovnice v úloze a) dosadit tento údaj. Vzniklou rovnici už jednoduše vyřešíte.
Řešení nápovědy 3
Do rovnice
\[ x = 100 e^{-0{,}02828t} \]
dosadíme za x = 50 g :
\[ 50 = 100 e^{-0{,}02828t} \] \[ \frac{1}{2} = e^{-0{,}02828t}, \]
zlogaritmujeme
\[ \ln (\frac{1}{2}) =\ln( e^{-0{,}02828t}) \] \[ \ln (\frac{1}{2}) = -0{,}02828t, \]
dostáváme přibližný výsledek:
\[ t = 24{,}5.\]
Z thoria zůstane nerozpadlých 50 gramů po 24,5 dnech.

Poznámka: Určili jsme, že přibližně polovina daného izotopu thoria se rozpadne po 24,5 dnech. Přibližně jsme tedy určili poločas rozpadu izotopu ²³⁴Th.
Nápověda 4 ( k úloze d) )
Úlohou je zvolit si několik hmotností (menších nebo rovných 100 g) dosud nerozpadlého thoria a z časové závislosti (vypočtené v úloze a) ) určit jim odpovídající časy.

Například při volbě 100 g, 90 g, 80 g atd. je potřeba určit čas, za který ze 100 g zůstane 90 g thoria, dále čas, za který zůstane 80 g thoria atd..

Při výpočtu postupujte analogicky jako v úloze c). Hodnoty je vhodné zapsat do přehledné tabulky. Graf z nich už pak jednoduše sestrojíte.
Řešení nápovědy 4
Několik libovolně zvolených hmotností (menších nebo rovných 100 g) dosud nerozpadlého thoria a jim příslušející časy jsou uvedeny níže v Tabulce č. 1.

Poznámka: Například 3,7 v tabulce označuje čas, za který ze 100 g thoria zůstane nerozpadlých 90 g.

Závislot hmotnosti thoria na čase je uvedená v Grafu č. 1.

Poznámka: Vypočtené časy jsou zaokrouhleny na jedno desetinné místo.
Celkové řešení
ad a)

Rovnice pro izotop thoria (²³⁴Th) vypadá následovně:
\[ \frac{\mathrm{d}x}{\mathrm{d}t}= -0{,}02828 x. \]
Provedeme integraci
\[ \frac {\mathrm{d}x}{x} = - 0{,}02828 \mathrm{d}t \] \[ \int\frac{\mathrm{d}x}{x} = -0{,}02828 \int \mathrm{d}t \] \[ \ln (\frac{x}{x_0}) = - 0{,}02828 t \]
Poznámka:V argumentu logaritmu jsme hmotnost x formálně vydělili konstantou x₀, která má rozměr hmotnosti, aby se v argumentu přirozeného logaritmu vyskytovala bezrozměrná veličina.

Aplikací exponenciály
\[ \frac{x}{x_0} = e^{-0{,}02828t}, \]
dostáváme výsledek
\[ x = x_0 e^{-0{,}02828t}. \]
Teď nezbývá nic jiného než určit konstantu x₀.

Víme, že v čase t = 0 bylo nerozpadlých 100 g thoria. Platí tedy
\[ 100 = x_0 e^{0}\hspace{20px} \Rightarrow \hspace{20px }x_0 = 100. \]
Výsledná závislost vypadá následovně:
\[ x (t) = 100 e^{-0{,}02828t}, \]
kde x je hmotnost v gramech, t je čas ve dnech.

ad b)

Naší úlohou je zjistit, kolik gramů thoria se rozpadne během 67 dnů.

Proto do rovnice
\[ x = 100 e^{-0{,}02828t} \]
za čas dosadíme t = 67:
\[ x (67) = 100 e^{-0{,}02828\cdot{67}} \]
Dostáváme přibližný výsledek:
\[ x = 15 \hspace{2px} \mathrm{g}. \]
Víme tedy, že ze 100 g thoria zůstalo nerozpadlých 15 g.

Během 67 dnů se rozpadne 85 g thoria.

ad c)

Do rovnice
\[ x = 100 e^{-0{,}02828t} \]
dosadíme za x = 50 g :
\[ 50 = 100 e^{-0{,}02828t} \] \[ \frac{1}{2} = e^{-0{,}02828t}, \]
zlogaritmujeme
\[ \ln (\frac{1}{2}) =\ln( e^{-0{,}02828t}) \] \[ \ln (\frac{1}{2}) = -0{,}02828t, \]
dostáváme přibližný výsledek:
\[ t = 24{,}5.\]
Z thoria zůstane nerozpadlých 50 gramů po 24,5 dnech.

Poznámka: Určili jsme, že přibližně polovina daného izotopu thoria se rozpadne po 24,5 dnech. Přibližně jsme tedy určili poločas rozpadu izotopu ²³⁴Th.

ad d)

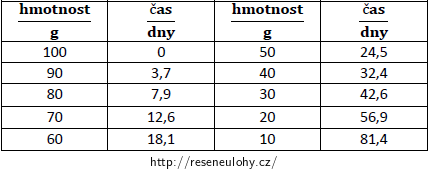
Několik libovolně zvolených hmotností (menších nebo rovných 100 g) dosud nerozpadlého thoria a jim příslušející časy jsou uvedeny níže v Tabulce č. 1.

Poznámka: Například 3,7 v tabulce označuje čas, za který ze 100 g thoria zůstane nerozpadlých 90 g.

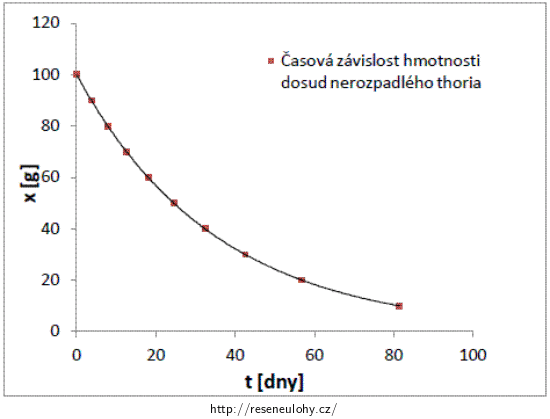
Závislot hmotnosti thoria na čase je uvedená v Grafu č. 1.

Poznámka: Vypočtené časy jsou zaokrouhleny na jedno desetinné místo.
Odpověď
a) Časová závislost hmotnosti daného izotopu thoria ²³⁴Th vypadá následovně:
\[ x = 100 e^{-0{,}02828t}, \]
kde x je hmotnost v gramech, t je čas ve dnech.

Poznámka: Uvedená rovnice je jen pro číselné hodnoty, bez fyzikální jednotky.

b) Během 67 dnů se rozpadne 85 g thoria.

c) Z thoria zůstane nerozpadlých 50 gramů po 24,5 dnech.

d) Z Grafu č. 1 (viz sekci Celkové řešení) je vidět, že časová závislost hmotnosti dosud nerozpadlého thoria vypadá jako graf exponenciální funkce.