Jedoucí kolo
Úloha číslo: 123
Kolo o poloměru R jede rovnoměrně přímočaře rychlostí v0. V systému souřadnic spojeném se zemí určete:
a) průběh polohového vektoru bodu X na obvodu kola,
b) průběh rychlosti bodu X a průběh její velikosti,
c) pomocí výsledku a) načrtněte tvar trajektorie a vypočtěte délku jednoho jejího oblouku,
d) určete délku uražené dráhy v závislosti na čase.
Nápověda 1: Obrázek situace
Zvolte vhodně souřadnicové osy a počátek soustavy souřadnic.
Nakreslete situaci pro čas t = 0 s. Počáteční polohu bodu X volte v počátku soustavy souřadnic.
Pak nakreslete situaci pro čas t a vyznačte polohu bodu X, kam až se za čas t dostal.
Vyznačte do obrázku dráhu, o kterou se kolo odvalilo za čas t. Jak je dlouhá?
Nápověda 2 pro a): Průběh polohového vektoru
Pohyb bodu X si rozložte na pohyb ve směru osy x a rotaci kolem bodu S.
Zkuste najít tři jednodušší vektory, s jejichž pomocí můžete polohový vektor \(\vec{PX}\) zapsat.
Nápověda 3 pro b): Průběh rychlosti a velikosti rychlosti
Jakým způsobem získáte z průběhu polohového vektoru bodu X průběh vektoru rychlosti bodu X? Zapište jej.
Jak z něj zjistíte průběh velikosti rychlosti bodu X?
Nápověda 4 pro c): Trajektorie pohybu, délka oblouku
Tvar trajektorie určete z průběhu polohového vektoru bodu X.
Nakreslete obrázek.
Znáte průběh velikosti rychlosti, jak spočtete délku jednoho oblouku, tedy dráhu uraženou za jednu otočku?
Nápověda 5 pro d): Uražená dráha v závislosti na čase
Víte, jakou dráhu urazí bod X za jednu periodu.
Dráhu uraženou za čas t < T umíte spočítat s pomocí vztahu pro průběh velikosti rychlosti.
Jak potom vyjádříte celkovou dráhu uraženou za libovolný čas t?
CELKOVÉ ŘEŠENÍ:
Obrázek situace:
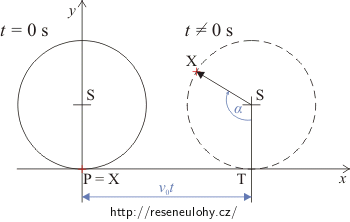
Stopky spustíme (t = 0 s) například v okamžiku, kdy se bod X dotýká vozovky. Tento bod na vozovce zvolíme za počátek P systému souřadnic. Osu x namíříme ve směru pohybu kola podél vozovky, osu y kolmo vzhůru.
Situaci v čase t = 0 s znázorňuje obrázek.
Za čas t se kolo odvalí o v0t ve směru osy x a vznikne situace znázorněná druhým obrázkem.
Z počátku P se bod X přemístí vlevo nahoru. Jestliže kolo neprokluzuje, je oblouk TX stejně velký jako odvalená dráha v0t. Orientovaný úhel TSX je roven: \[\alpha\,=\, -\omega{t}\,=\, -\frac{v_0t}{R}\,.\]
a) Polohový vektor
Polohový vektor \(\vec{PX}\,=\,\vec{r}\left(t\right),\) se poměrně složitě mění. Natahuje se doprava a střídavě se zvedá vzhůru a opět klesá. Tento vektor můžeme složit ze tří vektorů, které se chovají mnohem jednodušeji:
\[\vec{PX}\,=\,\vec{PT}+\vec{TS}+\vec{SX},\]\(\vec{PX}\) … se natahuje podél osy x rychlostí v0: \(\vec{PT}\,=\,v_0t\vec{\,i\,},\)
\(\vec{TS}\) … ční ve směru osy y: \(\vec{TS}\,=\,R\vec{\,j\,},\)
\(\vec{SX}\) … rovnoměrně rotuje ve směru hodinových ručiček kolem bodu S.
\[\vec{SX}\,=\,R\cos\left(-\frac{v_0t}{R}-\frac{\pi}{2}\right)\vec{\,i\,}+R\sin\left(-\frac{v_0t}{R}-\frac{\pi}{2}\right)\vec{\,j\,},\]kde \(\left(-\frac{v_0t}{R}-\frac{\pi}{2}\right)\) je orientovaný úhel, který svírá vektor \(\vec{SX}\) s osou x.
Dosazením do vztahu:
\[\vec{PX}\,=\,\vec{PT}+\vec{TS}+\vec{SX}\]a použitím vztahů:
\[\cos\left(-\alpha-\frac{\pi}{2}\right)\,=\,-\sin\alpha,\] \[\sin\left(-\alpha-\frac{\pi}{2}\right)\,=\,-\cos\alpha\]dostáváme pro polohový vektor \(\vec{r}\left(t\right) \,=\, \vec{PX}\):
\[\vec{PX}\,=\,\left(v_0t-R\sin\frac{v_0t}{R}\right)\vec{\,i\,}+\left(R-R\cos\frac{v_0t}{R}\right)\vec{\,j\,}.\]Případně ve složkách:
\[x\,=\,v_0t-R\sin\frac{v_0t}{R},\] \[y\,=\,R-R\cos\frac{v_0t}{R},\] \[z\,=\,0.\]b) Průběh vektoru rychlosti a velikosti rychlosti
Průběh vektoru rychlosti \(\vec{v}\left(t\right)\) určíme derivováním funkce \(\vec{r}\left(t\right)\):
\[\vec{r}\left(t\right) \,=\, \vec{PX}\,=\,\left(v_0t-R\sin\frac{v_0t}{R}\right)\vec{\,i\,}+\left(R-R\cos\frac{v_0t}{R}\right)\vec{\,j\,},\] \[\vec{v}\left(t\right)\,=\,\frac{\mathrm{d}\left(v_0t-R\sin\frac{v_0t}{R}\right)}{\mathrm{d}t}\vec{\,i\,}+\frac{\mathrm{d}\left(R-R\cos\frac{v_0t}{R}\right)}{\mathrm{d}t}\vec{\,j\,}.\]Po zderivování obdržíme pro průběh rychlosti:
\[\vec{v}\left(t\right)\,=\,\left(v_0-v_0\cos\frac{v_0t}{R}\right)\vec{\,i\,}+v_0\sin\frac{v_0t}{R}\vec{\,j\,}.\]Velikost rychlosti je absolutní hodnotou tohoto vektoru:
\[v\left(t\right)\,=\,\left|\vec{v}\left(t\right)\right|\,=\,\sqrt{v_\mathrm{x}^{2}+v_\mathrm{y}^{2}+v_\mathrm{z}^{2}}\,=\,\sqrt{\left(v_0-v_0\cos\frac{v_0t}{R}\right)^{2}+ \left(v_0\sin\frac{v_0t}{R}\right)^{2}},\] \[v\left(t\right)\,=\, \sqrt{v_0^2 - 2v_0^2{{\cos}\left(\frac{v_0t}{R}\right)} + v_0^{2}\left({\cos}^{2}\left(\frac{v_0t}{R}\right) + {\sin}^{2}\left(\frac{v_0t}{R}\right)\right)},\] \[v(t)= \sqrt{2v_0^{2} - 2v_0^{2}{\cos}(\frac{v_0t}{R})},\] \[v\left(t\right)\,=\, 2v_0\sqrt{\frac{1-\cos\frac{v_0t}{R}}{2}}.\]Nebo použitím vztahu \(\left|\sin\frac{\alpha}{2}\right|\,=\,\sqrt{\frac{1-\cos\alpha}{2}},\) zjednodušeně:
\[v\left(t\right)\,=\,2v_0\left|\sin\frac{v_0}{2R}t\right|.\]c) Trajektorie a délka jednoho oblouku
Trajektorii určíme nejpohodlněji například ze složek vektoru \(\vec{PX}\):
\[x\,=\,v_0t-R\sin\frac{v_0t}{R},\] \[y\,=\,R-R\cos\frac{v_0t}{R},\] \[z\,=\,0.\]Určíme několik bodů (x, y) trajektorie například pro časy 0, \(\frac{T}{6}\), \(\frac{2T}{6}\), \(\frac{3T}{6}\) atd.
Pro zjednodušení numerického výpočtu předpokládáme \(R\,=\,1\,\mathrm{m}\) a \(v\,=\,1\,\mathrm{m \cdot s^{-1}}.\)
Ze vztahů
\[ x\,=\,v_0t-R\sin\frac{v_0t}{R},\] \[y\,=\,R-R\cos\frac{v_0t}{R},\] \[z\,=\,0\]pak dostáváme:
x 0 0,18 1,23 3,13 5,05 6,10 6,28 y 0 0,5 1,5 2,0 1,5 0,5 0 Délka jednoho oblouku je rovna dráze uražené bodem za jednu periodu, tedy:
\[s_T\,=\,\int_0^{T}{v(t)}\,\mathrm{d}t,\]kde \(v\left(t\right) \,=\, 2v_0\left|\sin\frac{v_0}{2R}t\right|.\)
Jedna perioda je rovna \(T\,=\,\frac{2\pi{R}}{v_0}\). V intervalu od 0 do T nabývá \(\sin\frac{v_0}{2R}t\) kladných hodnot, takže není třeba psát absolutní hodnotu:
\[s_T\,=\,\int_0^{T}\left({2v_0\sin\frac{v_0}{2R}t}\right)\mathrm{d}t \,=\, 2v_0\frac{2R}{v_0}\left[-\cos\frac{v_0t}{2R}\right]_0^{T},\] \[s_T \,=\, 4R\left(-\cos\frac{v_02\pi{R}}{2Rv_0} + 1\right) \,=\, 8R. \]Délka jednoho oblouku je tedy: \(s_T\, =\, 8R\)
d) Uražená dráha v závislosti na čase
Pro odkutálení o víc než jednu obrátku získáme celou dráhu jako součet drah celých otoček a zbytku.
Víme, že délka jednoho oblouku je \(s_T\,=\,8R.\)
Dráha celých otoček je rovna:
\[s_\mathrm{c}\,=\,\left(INT\frac{t}{T}\right)\cdot 8R,\]kde \(INT\frac{t}{T}\) je celočíselná část podílu \(\frac{t}{T}.\)
Zbylou dráhu spočítáme ze vztahu:
\[s_\mathrm{z}\,=\,\int_0^{t_\mathrm{z}}{v(t)}\,\mathrm{d}t,\]kde \(v\left(t\right) \,=\, 2v_0\left|\sin\frac{v_0}{2R}t\right|.\)
Jedna perioda je rovna \(T\,=\,\frac{2\pi{R}}{v_0}\). V intervalu od 0 do T nabývá \(\sin\frac{v_0}{2R}t\) kladných hodnot a tz < T, takže není třeba psát absolutní hodnotu.
\[s_\mathrm{z}\,=\,\int_0^{t_\mathrm{z}}{2v_0\left|\sin\frac{v_0}{2R}t\right|}\mathrm{d}t\,=\,2v_0\frac{2R}{v_0}\left[-\cos\frac{v_0t}{2R}\right]_0^{t_\mathrm{z}},\] \[s_\mathrm{z}\, =\,4 R\left(1-\cos\frac{v_0t_\mathrm{z}}{2R}\right)\,=\,8R\sin^{2}\frac{v_0t_\mathrm{z}}{4R}.\]Celá dráha uražená za čas t je pak rovna:
\[s\left(t\right)\,=\,\left(INT\frac{t}{T}\right)\cdot 8R+8R\sin^{2}\frac{v_0t_\mathrm{z}}{4R}.\]První člen zde představuje součty celých obloučků, druhý člen příslušnou část posledního, neúplného obloučku.
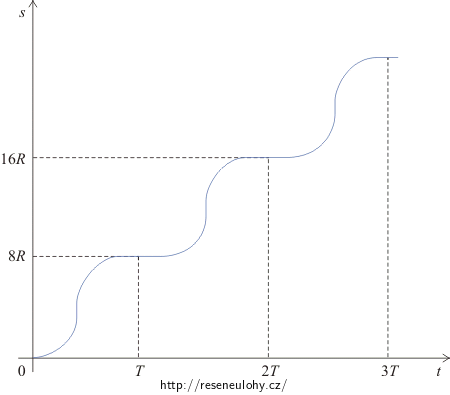
Graf funkce \(s\left(t\right)\,=\,\left(INT\frac{t}{T}\right)\cdot 8R+8R\sin^{2}\frac{v_0t_\mathrm{z}}{4R}\) má tento průběh:
Odpověď
a) Pro průběh polohového vektoru bodu X na obvodu kola platí:
\[\vec{r}\left(t\right) \,=\, \vec{PX}\,=\,\left(v_0t-R\sin\frac{v_0t}{R}\right)\vec{\,i\,}+\left(R-R\cos\frac{v_0t}{R}\right)\vec{\,j\,},\]případně ve složkách:
\[x\left(t\right) \,=\, v_0t-R\sin\frac{v_0t}{R},\] \[y\left(t\right) \,=\, R-R\cos\frac{v_0t}{R},\] \[z\left(t\right) \,=\, 0.\]b) Pro průběh rychlosti bodu X platí:
\[\vec{v}\left(t\right)\,=\,\left(v_0-v_0\cos\frac{v_0t}{R}\right)\vec{\,i\,}+v_0\sin\frac{v_0t}{R}\vec{\,j\,}.\]Velikost rychlosti bodu X je:
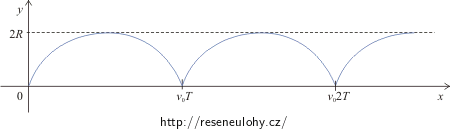
\[v\left(t\right)\,=\,\left|\vec{v}\left(t\right)\right|\,=\,\sqrt{v_\mathrm{x}^{2}+v_\mathrm{y}^{2}+v_\mathrm{z}^{2}}\,=\,2v_0\left|\sin\frac{v_0}{2R}t\right|.\]c) Tvar trajektorie je:
Délka jednoho oblouku je: \(s_T\,=\, 8R.\)
d) Délka uražené dráhy v závislosti na čase je:
\[s\left(t\right)\,=\,\left(INT\frac{t}{T}\right)\cdot 8R+8R\sin^{2}\frac{v_0t_\mathrm{z}}{4R},\]kde \(INT\frac{t}{T}\) je celočíselná část podílu \(\frac{t}{T}\) a \(t_\mathrm{z} \,=\,t - \left(INT\frac{t}{T}\right)T.\)
(První člen zde představuje součty celých obloučků, druhý člen příslušnou část posledního, neúplného obloučku.)
Vizualizace pomocí apletu
Kliknutím na tlačítko „Zapnout animaci“ se spustí animace, opětovné kliknutí tuto animaci zastaví. Čas \(t\) je možné měnit na posuvníku. Tlačítko „Zapnout stopu“ zapíná/vypíná stopu bodu X. Po zaškrtnutí tlačítka „Zobrazit trajektorii bodu X“ se zobrazí trajektorie bodu X bez nutnosti vykreslení stopou bodu X. Zaškrtnutí tlačítka „Zobrazit graf \(s(t)\)“ se uprostřed apletu vykreslí graf závislosti uražené dráhy bodu X na čase \(t\). Tlačítko „Reset“ zastaví animaci a vrátí aplet do původního stavu.
Trajektorie bodu X se nazývá cykloida.