Hráz přehrady
Úloha číslo: 1037
Určete, jak velkou silou působí voda na hráz říční přehrady (viz obrázek níže) tvaru rovnoramenného lichoběžníka o dolní základně z1, horní základně z2 a výšce H. Úlohu řešte nejdřív obecně, pak pro přehradu o výšce 220 m, délce dolní základně 195 m a délce horní základně 380 m.
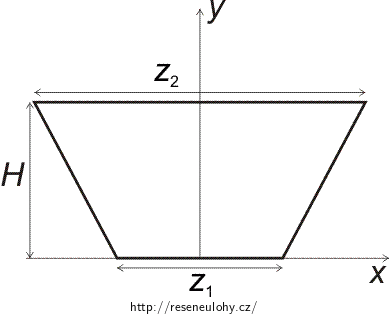
Poznámka: V zadání jsou uvedeny údaje skutečné přehrady s názvem Hoover Dam na řece Colorado v USA, jejíž tvar lze přibližně považovat za rovnoramenný lichoběžník.
Poznámka
V zadání jsou uvedeny údaje skutečné přehrady s názvem Hoover Dam na řece Colorado v USA (viz fotografii níže).

Nápověda 1
Úlohou je určit velikost síly, jakou působí voda na hráz přehrady.
Je zřejmé, že velikost síly závisí na hloubce h pod hladinou vody. Velikost celkové síly na přehradu bude dána součtem elementárních příspěvků, které závisí na hloubce h. Zkuste využít definici tlaku a vztah pro hydrostatický tlak.
Nápověda 2
Ve vztahu pro výpočet velikosti síly F se vyskytuje neznámá z (šířka přehrady v hloubce h).
Zkuste vyjádřit šířku z pomocí údajů z1, z2, H a h.
Zkuste při tom využít podobnost trojúhelníků, které v obrázku lehce naleznete.
Po vyjádření šířky přehrady z pak už integrál jednoduše spočítáte.
Řešení pro konkrétní hodnoty
Nyní spočteme přibližnou velikost síly, která působí na Hoover Dam na řeke Colorado.
Diskuze
Spočetli jsme, že voda působí na hráz přehrady Hoover Dam sílou velkou příbližně 61 GN. Nyní se zkusíme zamyslet nad velikostí této síly. V tabulce níže je uvedeno několik předmětů, jejich hmotnost m, tíhová síla FG, jaká působí v jejich těžišti a také počet předmětů N, jejichž tíhová síla by byla srovnatelná se sílou 61 GN.
Poznámka: Údaje v tabulce jsou zaokrouhleny.
předmět m / kg FG / N N / ks pytlík mouky 1 10 6.109 lokomotiva 8·104 8·105 8·104 Titanic 5·107 5·108 120 Celkové řešení
Již ze střední školy je známý vztah pro hydrostatický tlak
\[ p_h = \frac{F}{S} = h \rho g , \]kde F je velikost síly působící kolmo na plochu o obsahu S, ρ je hustota kapaliny, h je hloubka pod hladinou a g je velikost tíhového zrychelní.
Vyjádřením velikosti síly dostáváme
\[ F = S h \rho g. \]Naší úlohou je zjistit velikost síly F, která působí na přehradu. Tu získáme sečtením elementárních příspěvků dF, které označují velikost síly působící na úsek přehrady v hloubce h pod hladinou o elementární výšce dh a šířce z (viz obrázek níže).
Pro elementární velikost síly platí
\[ \mathrm{d}F = h \rho g\,\mathrm{d}S , \]kde dS je obsah plochy přehrady o elementární výšce dh a šířce z.
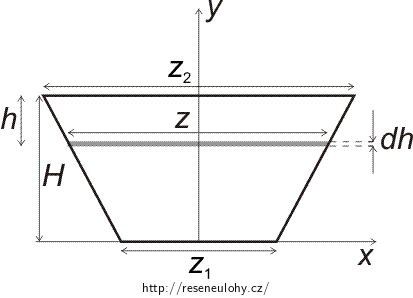
Velikost celkové síly získáme tedy integrací v mezích 0 až H
\[ F = \int_0^H\,\mathrm{d}F = \int_0^H h \rho g\, \mathrm{d}S. \]Po dosazení za dS (viz obrázek výše) dostáváme
\[ F = \int_0^H h \rho g \underbrace{z \,\mathrm{d}h}_{\mathrm{d}S}. \]Ve vztahu pro velikost síly F se vyskytuje šířka přehrady z v hloubce h, kterou potřebujeme vyjádřit. Vyjdeme z podobnosti pravoúhlých trojúhelníků, které jsou zakresleny v obrázku níže.
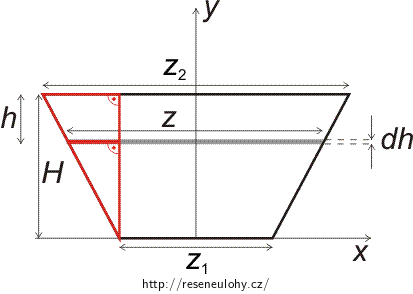
Z podobnosti pravoúhlých trojúhelníků znázorněných v obrázku červeně plyne
\[ \frac{\frac{z_2 - z_1}{2}}{H} = \frac{\frac{z - z_1}{2}}{H - h} \]a po vynásobení dvěma dostáváme
\[ \frac{z_2 - z_1}{H} = \frac{z - z_1}{H - h}. \]Nyní vyjádříme z
\[ (z_2 - z_1)(H - h) = H(z - z_1) \] \[ (z_2 - z_1)(H - h) = Hz - Hz_1 \] \[ (z_2 - z_1)(H - h) + Hz_1 = Hz \] \[ Hz_2 - Hz_1 -(z_2 - z_1)h + Hz_1 = Hz \] \[ z = z_2 -(z_2 - z_1)\frac{h}{H}. \]Dosadíme získaný vztah do vztahu pro velikost síly F a provedeme integraci
\[ F = \int_0^H h \rho g z \mathrm{d}h = \rho g \int_0^H h\left[z_2 -(z_2 - z_1)\frac{h}{H}\right] \mathrm{d}h = \rho g \int_0^H \left[hz_2 -(z_2 - z_1)\frac{h^2}{H}\right]\mathrm{d}h = \] \[=\rho g \left[ \frac{h^2}{2}z_2 - \frac{h^3}{3H}(z_2 - z_1)\right]_0^H = \rho g \bigg(\frac{H^2}{2}z_2 - \frac{H^3}{3H}(z_2 - z_1)\bigg) = \rho g \bigg( \frac{H^2}{2}z_2 - \frac{H^2}{3}z_2 + \frac{H^2}{3}z_1 \bigg). \]Pro velikost výsledné síly, která působí na přehradu, platí
\[F = \frac{1}{3}\rho g H^2 \left(z_1 + \frac{z_2}{2}\right).\]Nyní spočteme přibližnou velikost síly, která působí na Hoover Dam na řeke Colorado.
Do vztahu pro velikost síly působící na hráz přehrady
\[F = \frac{1}{3}\rho g H^2 \left(z_1 + \frac{z_2}{2}\right),\]dosadíme známé údaje:
\[ F = \bigg[\frac{1}{3} \cdot {1000}\cdot {9{,}81} \cdot {220}^2 \left(195 + \frac{380}{2}\right)\bigg]\, \mathrm N \stackrel{\cdot}{=} 6{,}09 \cdot {10}^{10}\,\mathrm N. \]Voda působí na přehradu Hoover Dam sílou \[F \stackrel{\cdot}{=} 61\,\mathrm{GN}.\]
Odpověď
Voda působí na hráz říční přehrady silou
\[F = \frac{1}{3}\rho g H^2 \left(z_1 + \frac{z_2}{2}\right).\]Na přehradu Hoover Dam působí voda přibližně sílou F = 61 GN.

