Vektorový potenciál dlouhého drátu
Úloha číslo: 244
(a) Najděte vektorový potenciál pro magnetické pole v okolí dlouhého tenkého drátu, kterým teče proud I. Ověřte, že platí \(\nabla\cdot\vec A = 0\).
(b) Najděte vektorový potenciál magnetického pole uvnitř i vně tlustého válcového drátu poloměru R, jestliže proud I je rovnoměrně rozprostřen celým průřezem drátu.
První nápověda k části (a)
Uvědomte si, že magnetická indukce \(\vec B\) a vektorový potenciál \(\vec A\) jsou spjaty vztahem
\[\vec B = \nabla\times \vec A.\]Magnetickou indukci, určenou například pomocí Ampérova zákona, vyjádřete ve válcových souřadnicích, přičemž osu z umístěte do drátu ve směru proudu. Operátor rotace ve válcových souřadnicích vypadá následovně:
\[\vec B = \nabla\times\vec A = \left(\frac{1}{s}\frac{\partial A_\mathrm{z}}{\partial\phi}-\frac{\partial A_\mathrm{\phi}}{\partial z},\ \frac{\partial A_\mathrm{s}}{\partial z}-\frac{\partial A_\mathrm{z}}{\partial s},\ \frac{1}{s}\frac{\partial (sA_\phi)}{\partial s}-\frac{\partial A_\mathrm{s}}{\partial\phi}\right).\]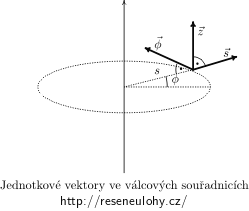
Dále si uvědomte, že proudový element \(\mathrm{d}\vec I\) v místě \(\vec r^,\) budí v místě \(\vec r\) vektorový potenciál
\[\mathrm{d}\vec A = \frac{\mu_0}{4\pi}\frac{\mathrm{d}\vec I}{|\vec r-\vec r^,|}.\]Proud je v našem případě konstantní a má všude stejný směr. Z toho dostáváme, že vektorový potenciál musí mít ve všech místech stejný směr jako proud I. Protože proud má směr osy z, vyplývá odtud, že složky \(A_\mathrm{s} = A_\phi = 0\) a pouze složka \(A_\mathrm{z}\) je nenulová.
Poznámka: Předchozí zdůvodnění o směru vektorového potenciálu má jednu vadu. V našem případě neklesá v nekonečnu hodnota proudu k nule, a proto vztah
\[\vec A = \frac{\mu_0}{4\pi}\int_V \frac{\mathrm{d}\vec I}{|\vec r-\vec r^,|}\]nelze pro určení vektorového potenciálu použít, neboť integrál diverguje. Přesněji bychom tedy měli říci, že nulovost složek budeme předpokládat a u nalezeného řešení posléze ověříme, že splňuje rovnosti
\[\nabla\times\vec A = \vec B, \qquad \nabla\cdot\vec A = 0.\]Druhá nápověda k části (a)
Využijeme vztah mezi magnetickou indukcí a vektorovým potenciálem
\[\vec B = \nabla\times\vec A.\]Vztah pro rotaci vektorového potenciálu se velmi zjednoduší použitím válcových souřadnic, neboť v nich má vektorový potenciál nenulovou jedinou složku. Vektor magnetické indukce \(\vec B\) má ve válcových souřadnicích též jedinou nenulovou složku, a to složku \(B_\phi\). Dostaneme tedy jednu jednoduchou diferenciální rovnici, z níž vypočteme hledanou nenulovou složku vektorového potenciálu \(A_\mathrm{z}\).
Rozbor části (a)
Známe, respektive například pomocí Ampérova zákona s využitím symetrie umíme jednoduše spočítat, magnetickou indukci v okolí dlouhého drátu. Víme, že magnetická indukce je rotací vektorového potenciálu, což je obecně soustava tří diferenciálních rovnic. Vzhledem k symetrii situace je ale vysoce pravděpodobné, že v této soustavě bude „mnoho koeficientů nulových“.
Protože navíc víme, že magnetická indukce „cirkuluje“ kolem drátu a vektorový potenciál má směr proudu, je výhodné použít válcových souřadnic (kde osu z umístíme do drátu), neboť v těchto souřadnicích budou mít vektory magnetické indukce i vektorového potenciálu nenulovou pouze jedinou složku.
Řešení části (a)
Budeme počítat ve válcových souřadnicích, kde osu z ztotožníme s drátem. V této soustavě souřadnic se totiž dobře popisuje magnetická indukce, která „obíhá“ kolem drátu. Platí, že
\[\vec B = \frac{\mu_0I}{2\pi s}\vec\phi,\]kde \(\vec\phi\) značí jednotkový vektor mající směr tečny ke kružnici, která leží v rovině kolmé na drát (osu z) a má střed v drátu (viz obrázek).

Operátor rotace aplikovaný na vektorový potenciál \(\vec A\) ve válcových souřadnicích \((s,\,\phi,\,z)\) dává následující složky:
\[\vec B = \nabla\times\vec A = \left(\frac{1}{s}\frac{\partial A_\mathrm{z}}{\partial\phi}-\frac{\partial A_\phi}{\partial z},\ \frac{\partial A_\mathrm{s}}{\partial z}-\frac{\partial A_\mathrm{z}}{\partial s},\ \frac{1}{s}\frac{\partial (sA_\phi)}{\partial s}-\frac{\partial A_\mathrm{s}}{\partial\phi}\right).\]Z integrálního vztahu pro vektorový potenciál
\[\vec A(\vec r) = \frac{\mu_0}{4\pi}\int_V \frac{d\vec I^,}{|\vec r-\vec r^,|}\]vidíme, že pro konstantní proud přímým vodičem má vektorový potenciál ve všech místech stejný směr jako proud I.
Proto jsou v našem případě složky vektorového potenciálu \(A_\mathrm{s}\) a \(A_\phi\) nulové, jedinou nenulovou složkou je \(A_\mathrm{z}\). Z válcové symetrie a z toho, že drát je nekonečně dlouhý, navíc plyne, že složka \(A_\mathrm{z}\) může záviset pouze na vzdálenosti s od drátu, nikoliv na úhlu \(\phi\). Tudíž ve vyjádření rotace vektorového potenciálu ve válcových souřadnicích je nenulová pouze jedna derivace
\[B_\phi = -\frac{\partial A_\mathrm{z}}{\partial s},\] \[\frac{\mu_0I}{2\pi s} = -\frac{\partial A_\mathrm{z}}{\partial s}\]a odtud dostáváme integrací
\[A_\mathrm{z} = -\frac{\mu_0I}{2\pi}\ln(s/a),\]kde za konstantu a můžeme volit libovolné kladné číslo.
Ještě ověříme nulovost divergence \(\vec A\). Ve válcových souřadnicích platí, že
\[\nabla\cdot\vec A = \frac{1}{s}\frac{\partial}{\partial s}(sA_\mathrm{s}) + \frac{1}{s}\frac{\partial A_\phi}{\partial\phi} + \frac{\partial A_\mathrm{z}}{\partial z} = 0+0+0 = 0,\]neboť složky \(A_\mathrm{s}\) a \(A_\phi\) jsou nulové a složka \(A_\mathrm{z}\) nezávisí na proměnné z.
Nápověda k části (b)
Nejprve určete magnetickou indukci uvnitř válcového vodiče. K tomu využijte Ampérova zákona celkového proudu
\[\oint_\mathrm{c} \vec B\cdot d\vec s = \mu_0I\]aplikovaného na kruhovou smyčku obepínající osu vodiče a faktu, že magnetická indukce rotuje kolem osy obdobně jako v případě tenkého vodiče umístěného v ose.
Pokuste se také tento fakt odůvodnit použitím symetrie.
Po spočtení magnetické indukce pak aplikujte stejnou techniku jako v části (a). Vně vodiče navíc není co počítat, neboť magnetická indukce vně vodiče je určena stejnými vztahy jako v části (a), a tedy i vektorový potenciál bude stejný.
Odkaz na podobnou úlohu
Výpočet magnetické indukce uvnitř plného tlustého vodiče je speciálním případem úlohy Dutý válcový vodič.
Rozbor části (b)
Výsledky části (a) můžeme použít na oblast vně drátu, neboť tlustý dlouhý válcový drát s rovnoměrně rozloženým proudem budí vně sebe stejné magnetické pole jako tenký drát. Vyplývá to z Ampérova zákona: stejně jako u tenkého dlouhého drátu je problém válcově symetrický a v Ampérově zákoně lze použít integraci přes kruhovou smyčku obepínající tlustý drát se středem v jeho ose. Integrál přes smyčku na levé straně Ampérova zákona zůstane stejný jako u tenkého drátu a celkový proud na pravé straně se taktéž nezmění.
Magnetickou indukci uvnitř drátu můžeme určit podle Ampérova zákona celkového proudu. Opět je výhodné provést to ve válcových souřadnicích.
Představíme-li si tlustý drát jako nekonečné množství tenkých drátů, v nichž proud míří vzhůru ve směru kladné poloosy z, je zřejmé, že magnetická indukce bude mít nulovou z-ovou složku; neboť tenký drát s proudem ve směru osy z budí magnetické pole, jehož magnetická indukce je ve směru osy z nulová.
Podobnou úvahou dostaneme, že také radiální složka je nulová. Můžeme argumentovat třeba takto: k libovolnému „tenkému drátu“ budícímu pole s nenulovou radiální složkou v daném místě existuje symetricky umístěný drát (umístěný zrcadlově vzhledem k rovině určené osou z a daným místem), který budí magnetické pole o stejné velikosti. Výsledné magnetické pole obou drátů má nenulovou pouze tečnou složku (viz obrázek a podrobný komentář pod ním).
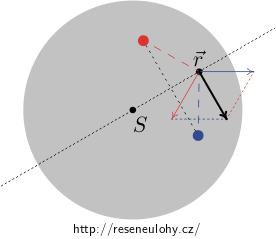
Určujeme magnetickou indukci uvnitř tlustého válcového drátu v bodě určeném polohovým vektorem \(\vec r\). Osa drátu prochází bodem S a je kolmá na obrazovku, proud teče ve směru do obrazovky. Ukážeme, že magnetická indukce má nulovou radiální složku. Ke každému tenkému „červenému“ drátu v průřezu válce totiž najdeme symetricky „modrý“ drát a jejich radiální složky magnetické indukce se navzájem budou rušit.
Jediná nenulová složka magnetické indukce tedy má směr vektoru \(\vec\phi\). Z válcové symetrie pak vyplývá, že její velikost může záviset pouze na vzdálenosti s od osy z. Proto podél kruhové smyčky o poloměru s < R má magnetická indukce konstantní velikost B(s) a stejnou orientaci (magnetická indukce je s výjimkou materiálových rozhraní spojitá vektorová funkce, takže není možné, aby se orientace náhle změnila na opačnou).
To nám umožní jednoduše určit magnetické pole pomocí Ampérova zákona celkového proudu použitého na kruhovou smyčku obepínající osu drátu.
Ostatní úvahy zůstávají stejné jako v části (a). Z analogického důvodu bude mít vektorový potenciál směr osy z a můžeme použít stejnou techniku výpočtu.
Řešení části (b)
Opět budeme počítat ve válcových souřadnicích. Osu z volíme shodnou s osou válcového vodiče a její kladný směr orientujeme do směru proudu.
Vně válcového vodiče můžeme použít výsledky části (a), neboť tlustý nekonečný válcový vodič budí vně sebe stejné pole jako vodič tenký, kterým prochází stejný celkový proud.
V oblasti uvnitř vodiče k magnetické indukci ve vzdálenosti s od osy přispívá pouze vnitřní válec o poloměru s; magnetické pole uvnitř vodiče je opět tzv. cirkumferentální — to značí, že vektor magnetické indukce „obíhá“ kolem osy vodiče a jeho velikost závisí pouze na vzdálenosti od osy. Použijeme Ampérův zákon
\[\oint_\mathrm{c} \vec B\cdot d\vec s = \mu_0I^, ,\]který aplikujeme na kruhovou smyčku o poloměru s se středem v ose vodiče a jako I' jsme označili proud procházející plochou smyčky, pro který platí
\[I^, = \frac{I}{\pi R^2}\cdot S = \frac{I}{\pi R^2}\cdot \pi s^2 = I\frac{s^2}{R^2}.\]Protože magnetická indukce má ve vzdálenosti s od osy konstantní orientaci i velikost B(s), dostáváme z Ampérova zákona
\[B(s)\cdot (2\pi s) = \mu_0I^,\] \[B(s)\cdot (2\pi s) = \mu_0I\frac{s^2}{R^2},\]a tedy
\[B(s) = \frac{\mu_0}{2\pi}\frac{Is}{R^2}.\]Z obdobných úvah jako v části (a) vyplývá, že vektorový potenciál \(\vec A\) bude mít jedinou nenulovou složku ve směru proudu, tedy složku Az. Analogicky jako v části (a) tak dostáváme diferenciální rovnici
\[-\frac{\partial A_\mathrm{z}}{\partial s} = B(s),\] \[\frac{\partial A_\mathrm{z}}{\partial s} = -\frac{\mu_0}{2\pi }\frac{Is}{R^2},\]kterou lze řešit integrací
\[A_\mathrm{z} = -\frac{\mu_0I}{4\pi R^2}s^2+C,\]kde C je integrační konstanta. Tu pišme ve tvaru
\[C = \frac{\mu_0I}{4\pi R^2}b^2,\]důvod k tomu bude zřejmý níže. Dostáváme tak vztah
\[A_\mathrm{z} = -\frac{\mu_0I}{4\pi R^2}(s^2-b^2).\]Konstanta b je podobně jako konstanta a libovolná, ale vektorový potenciál musí být spojitý na rozhraní vodič–vzduch, musí tedy nastat rovnost ve vztazích
\[-\frac{\mu_0I}{2\pi}\ln\frac{s}{a} = -\frac{\mu_0I}{4\pi R^2}(s^2-b^2)\]pro s = R. To vede na podmínku
\[2\ln(R/a) = 1-(b/R)^2.\]Jednou (nikoli však jedinou) možností je volit a=b=R, pak dostaneme
\[A = A_\mathrm{z} = -\frac{\mu_0I}{4\pi R^2}(s^2-R^2) \qquad {\rm pro }\ s\leq R,\] \[A = A_\mathrm{z} = -\frac{\mu_0I}{2\pi}\ln\frac{s}{R} \qquad {\rm pro }\ s \geq R.\]Obrázek k části (b) – magnetická indukce a vektorový potenciál
Magnetická indukce obíhá uvnitř drátu kolem svislé osy a její velikost s rostoucí vzdáleností od osy lineárně roste. Vně drátu vektor magnetické indukce cirkuluje stejně jako uvnitř drátu, ale jeho velikost s rostoucí vzdáleností od osy klesá.
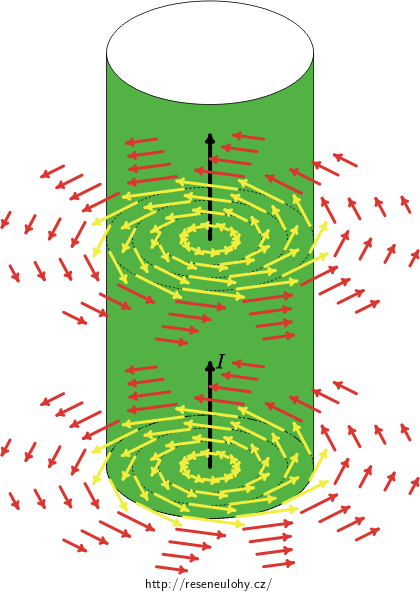
Žlutě jsou vyznačeny vektory magnetické indukce uvnitř drátu, červeně vektory magnetické indukce vně drátu.
Uvnitř drátu má vektorový potenciál stejnou orientaci jako proud. Největší je v ose vodiče. Při zvolených konstantách je na hranici vodiče nulový. Vně vodiče jeho velikost s rostoucí vzdáleností od osy logaritmicky roste a jeho orientace je opačná vůči proudu.
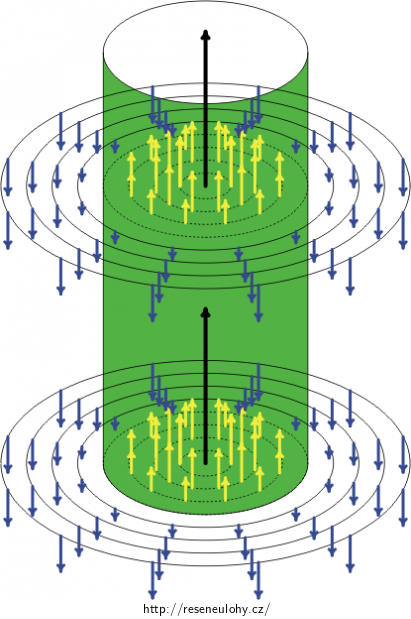
Žlutě je vyznačen vektorový potenciál uvnitř drátu, modře vektorový potenciál vně drátu.
Odpověď
(a) Pro dlouhý tenký přímý drát, kterým protéká proud I, platí, že vektorový potenciál \(\vec A\) má v každém místě směr shodný se směrem proudu a má velikost
\[A = -\frac{\mu_0I}{2\pi}\ln\frac{s}{a},\]kde konstantu a lze volit libovolnou kladnou.
(b) Pro vnější oblast tlustého drátu platí stejné vztahy jako pro tenký drát v jeho ose, kterým protéká stejný celkový proud. Pro s > R má tedy vektorový potenciál \(\vec A\) v každém místě směr shodný se směrem proudu a má velikost
\[A = - \frac{\mu_0I}{2\pi}\ln\frac{s}{a}, \qquad s > R\mathrm{,}\tag{1}\]kde konstantu a lze volit libovolnou kladnou.
Pro oblast uvnitř drátu platí, že vektorový potenciál \(\vec A\) má směr shodný se směrem proudu (stejně jako v jeho okolí) a má velikost
\[A = -\frac{\mu_{0} I}{4 \pi R^2}(s^2-b^2)\mathrm{,} \qquad s < R \mathrm{,}\tag{2}\]kde konstantu b lze volit libovolně, s přihlédnutím k podmínce, že vektorový potenciál je spojitá funkce, a proto musí být splněna rovnost vztahů (1) a (2) pro s=R.
Jedna možnost, nikoli však jediná, je volit a = b = R.




