Moment setrvačnosti asteroidy
Úloha číslo: 2134
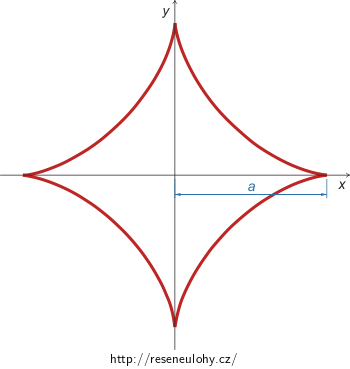
Určete moment setrvačnosti homogenní asteroidy vůči ose y.
Zadána je délka jednoho ramene asteroidy a a její celková hmotnost m.
Nápověda
Tato úloha není výkladová, pokud zjistíte, že máte s určitými partiemi problémy, doporučujeme projít si nejprve úlohy Těžiště cykloidy a Délka asteroidy, na kterou tato úloha přímo navazuje. V úloze Délka asteroidy je vysvětleno, co asteroida je, a jaké má parametrické rovnice. Určitou nápovědu může poskytnout také Délka oblouku cykloidy.
Rozbor
Úlohu začneme řešit vyjádřením momentu setrvačnosti J obecného tuhého tělesa vůči dané ose otáčení. Toto vyjádření budeme postupně upravovat do podoby, kterou dokážeme integrovat. Během řešení využijeme vztah pro délku obecné křivky, parametrické vyjádření asteroidy a jejich derivace i vztah pro délkovou hmotnostní hustotu. Poté provedeme integraci a na závěr nahradíme veličiny, které neznáme, těmi známými ze zadání.
Řešení
Vyjdeme ze vztahu pro moment setrvačnosti J tuhého spojitého tělesa vůči dané ose otáčení
\[J=\int_M r^2 \mathrm d m,\]kde r značí vzdálenost elementu hmotnosti dm od osy rotace a integrál znamená, že sčítáme momenty setrvačnosti hmotných elementů přes celé těleso o celkové hmotnosti M.
Jako první jednoduchou úpravu nahradíme veličinu r. Osa, vůči které počítáme moment setrvačnosti, je osa y, vzdálenost elementu hmotnosti od ní je proto jeho souřadnice x. Dostáváme
\[J=\int_M x^2 \mathrm d m.\]Dále nahrádíme integraci přes hmotnost. Jelikož asteroida je křivka, použijeme vztah pro délkovou hmotnostní hustotu \(\lambda:\)
\[\lambda = \frac{m}{s},\]kde s značí celkovou délku asteroidy. Ze vztahu vyjádříme hmotnost a použijeme diferenciální tvar
\[\mathrm d m = \lambda \mathrm d s,\]kde ds je délka elementu asteroidy o hmotnosti dm.
To nám po dosazení do vztahu pro moment setrvačnosti dá
\[J = \int_\Gamma x^2 \lambda \mathrm d s.\]V tomto vztahu nám \(\Gamma\) značí, že integrujeme přes celou křivku, tedy celou asteroidu.
Dále vyjádříme element délky ds pomocí souřadnic x a y. K tomu nám poslouží vztah pro element délky obecné křivky odvozený v úloze Délka oblouku cykloidy
\[ \mathrm{d} s= \sqrt{\left( \frac{\mathrm{d} x}{\mathrm{d} t} \right)^2+ \left( \frac{\mathrm{d} y}{\mathrm{d} t} \right)^2} \mathrm{d} t,\]kde t značí parametr.
Vztah pro ds dosadíme do vztahu pro moment setrvačnosti a dostaneme \[ J = \int_\Gamma x^2 \ \lambda \ \sqrt{\left( \frac{\mathrm{d} x}{\mathrm{d} t} \right)^2+ \left( \frac{\mathrm{d} y}{\mathrm{d} t} \right)^2} \mathrm{d} t.\tag{1}\]Nyní máme ve vztahu derivace i integraci podle parametru t, tedy potřebujeme vědět, jak se x,y mění s parametrem t – potřebujeme parametrické rovnice.
Tvar parametrických rovnic pro asteroidu je odvozen v úloze Délka asteroidy a je následující:
\[x = a \cos^3 t\] \[y = a \sin^3 t\] \[t \in (0;2\pi\rangle.\]Budeme potřebovat i derivace těchto rovnic
\[\frac{\mathrm{d}x}{\mathrm{d}t}=-3a\ \cos^2 t\ \sin t\] \[\frac{\mathrm{d}x}{\mathrm{d}t}=3a\ \sin^2 t\ \cos t.\]Po dosazení za neznámé x, y i jejich derivace do vztahu pro moment setrvačnosti (1) dostáváme
\[ J = \int_0^{2\pi} a^2 \ \lambda \ \cos^6 t \ \sqrt{9a^2 \ \cos^4 t \ \sin^2 t + 9 a^2 \ \sin^4 t \ \cos^2 t} \ \mathrm d t.\]Ze součtu pod odmocninou můžeme před odmocninu vytknout \(3a\cos{t}\sin{t}\), tím získáme
\[ J = \int_0^{2\pi} 3a^3 \ \lambda \ \cos^7 t \ \sin t \ \sqrt{\cos^2 t + sin^2 t} \ \mathrm d t.\]Pod odmocninou získáváme známý goniometrický výraz, tzv. „goniometrickou jedničku“. Zároveň vytkneme \(3a^3 \lambda\) před integrál, protože se jedná o konstantu. Dostaneme se na tvar
\[ J = 3a^3 \ \lambda \ \int_0^{2\pi} \cos^7 t \ \sin t \ \mathrm d t.\]Více náš vztah již zjednodušit nelze a především již dokážeme integrovat použitím substituce.
Substituci zvolíme následující
\[u = \cos^4 t\] \[\mathrm d u = -4 \cos^3 t \ \sin t\] \[-\frac{1}{4} \mathrm d u = \cos^3 t \ \sin t.\]Dále však narazíme na problém. Pokud se pokusíme přepočítat integrační meze, obě nám vyjdou rovny 1, což by dalo nulový celkový výsledek. To je zajisté špatně – má-li asteroida nenulovou hmotnost a nenulový rozměr a, jistě musí mít i nenulový moment setrvačnosti. Problém je zřejmě ve funkci \(\cos^4 t\), jelikož jde o periodickou funkci s periodou π a integrační meze jsou obě násobkem této periody. Tomuto problému se můžeme vyhnout díky symetriím, které asteroida má – je symetrická podle osy x i podle osy y. Tedy můžeme určit pouze moment setrvačnosti jedné čtvrtiny asteroidy a výsledek poté vynásobit čtyřmi. Tím se nám integrační meze pro integraci podle parametru t změní z 0 a 2π na 0 a π/2. Pro integraci podle u dostáváme meze 1 a 0 (stačí postupně dosadit meze pro parametr t do substituce).
\[J_{\frac{1}{4}}\,=\,3a^3 \ \lambda \ \int_1^0 -\frac{1}{4} u\ \mathrm d u\,=\,\frac{3}{4}a^3 \ \lambda \ \int_0^1 u\ \mathrm d u\,=\,\frac{3}{4}a^3\lambda {\left[\frac{u^2}{2}\right]}_0^1\,=\,\frac{3}{8}a^3\lambda\] \[J\,=\,4J_{\frac{1}{4}}\,=\,\frac{3}{2}a^3\lambda\]Na začátku úlohy jsme měli zadánu celkovou hmotnost asteroidy, ne její hustotu \(\lambda\). Pro přepočet délkové hustoty na hmotnost budeme potřebovat znát celkovou délku asteroidy, ta je vypočítána v úloze Délka asteroidy, kde je výsledkem
\[s=6a.\]Do vztahu pro moment setrvačnosti tedy můžeme dosadit vztah
\[\lambda = \frac{m}{6a}\]a získáme
\[J = \frac{1}{4} a^2 m.\]Odpověď
Moment setrvačnosti J asteroidy je
\[J = \frac{1}{4} a^2 m.\]

