Pohyb hmotného bodu

Úloha číslo: 980

Pohyb hmotného bodu je dán parametricky následujícími rovnicemi (jedná se o složky polohového vektoru v kartézském systému souřadnic):

\[ x(t)= \hspace{2px}4 \cos \hspace{1px} \left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right) \] \[ y(t)= -4 \sin \hspace{1px}\left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right), \]

kde t je čas.

a) Určete složky vektoru rychlosti.

b) Určete složky vektoru zrychlení.

c) Určete velikost vektoru rychlosti a pomocí ní určete tečnou složku zrychlení.

d) Zjistěte, po jaké trajektorii se hmotný bod pohybuje.

Poznámka: Uvedené rovnice jsou jen pro číselné hodnoty. V úloze se výpočty provádějí také jenom číselně, bez jednotek.

Nápověda 1 (k úloze a) )
Víme, že vektor rychlosti má směr tečny v každém bodě trajektorie. Na základě této skutečnosti si zkuste uvědomit vztah mezi složkami rychlosti a souřadnicemi polohy hmotného bodu.
Řešení nápovědy 1
Složky rychlosti získáme jednoduše derivací
\[ v_{\mathrm{x}}(t) = \frac{\mathrm{d}x(t)}{\mathrm{d}t} = -4 \sin\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right)\frac{2}{3}t = -\frac{8}{3}t\hspace{2px}\sin\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right) \hspace{1px} \] \[ v_{\mathrm{y}}(t) = \frac{\mathrm{d}y(t)}{\mathrm{d}t} = -4 \cos\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right)\frac{2}{3}t = \hspace{2px} -\frac{8}{3 }t\hspace{2px}\cos\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right). \]
Získali jsme tak vektor rychlosti
\[ \vec{v}= \left(-\frac{8}{3}t\hspace{2px}\sin\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right) \hspace{1px},\hspace{2px} -\frac{8}{3 }t\hspace{2px}\cos\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right)\hspace{1px}\right). \]
Nápověda 2 (k úloze b) )
K určení zrychlení je nutné uvědomit si vztah mezi složkami zrychlení a složkami rychlosti. Jedná se vlastně o analogický postup jako v úloze a).
Řešení nápovědy 2
Složky vektoru zrychlení získáme derivací složek rychlosti (derivace součinu)
\[ a_{\mathrm{x}}(t)= \frac{\mathrm{d}v_{\mathrm{x}}(t)}{\mathrm{d}t} = - \frac{8}{3} \sin \left(\frac{1}{3}t^2 + \frac{\pi}{2}\right)\hspace{1px}+\hspace{1px}\left[-\frac{8}{3}t\cos\left(\frac{1}{3}t^2+\frac{\pi}{2}\right)\frac{2}{3}t \right] =\] \[=- \frac{8}{3} \left[ \sin \left(\frac{1}{3}t^2 + \frac{\pi}{2}\right)+ \frac{2}{3}t^2 \cos\left(\frac{1}{3}t^2+\frac{\pi}{2}\right)\right] \] \[ a_{\mathrm{y}}(t)= \frac{\mathrm{d}v_{\mathrm{y}}(t)}{\mathrm{d}t} = - \frac{8}{3} \cos \left(\frac{1}{3}t^2 + \frac{\pi}{2}\right)\hspace{1px}+\hspace{1px}\frac{8}{3}t\sin\left(\frac{1}{3}t^2+\frac{\pi}{2}\right)\frac{2}{3}t =\] \[= - \frac{8}{3} \left[ \cos \left(\frac{1}{3}t^2 + \frac{\pi}{2}\right)- \frac{2}{3}t^2 \sin\left(\frac{1}{3}t^2+\frac{\pi}{2}\right)\right]. \]
Získali jsme tak složky vektoru zrychlení \[ \vec{a}= (a_{\mathrm{x}},\hspace{1px}a_{\mathrm{y}}). \]
Nápověda 3 ( k úloze c) )
Úlohou je určit velikost vektoru rychlosti. Stačí si uvědomit, že složky v_x a v_y jsou na sebe kolmé. Použijte tedy Pythagorovu větu.

Zkuste si rozmyslet, jak určíte tečnou složku zrychlení. Využijte při tom velikost rychlosti.
Řešení nápovědy 3
Velikost vektoru rychlosti získáme následovně (vycházíme přitom z Pythagorovy věty - viz obrázek):

\[ \left | \vec{v} \right| = \sqrt{v_{\mathrm{x}}^2+v_{\mathrm{y}}^2} \] \[ \left | \vec{v} \right|=\sqrt{\frac{64}{9}t^2\sin^2\left(\frac{1}{3}t^2+\frac{\pi}{2}\right) + \frac{64}{9}t^2\cos^2\left(\frac{1}{3}t^2+\frac{\pi}{2}\right)} \] \[ \left | \vec{v} \right|= \sqrt{\frac{64}{9}t^2 \underbrace{\left[\sin^2\left(\frac{1}{3}t^2+\frac{\pi}{2}\right)+ \cos^2\left(\frac{1}{3}t^2+\frac{\pi}{2}\right)\right]}_1} \] \[ \left | \vec{v} \right|= \frac{8}{3}t. \]
Tečnou složku zrychlení dostaneme derivací velikosti rychlosti podle času:
\[ a_{\mathrm{t}}= \frac{d\left|\vec{v}\right|}{dt}= \frac{8}{3}. \]
Nápověda 4 ( k úloze d) )
Úlohou je určit, po jaké trajektorii (křivce) se hmotný bod pohybuje. Z parametrického vyjádření křivky, které je uvedené v zadání, to ale nemusí být na první pohled vidět.

Zkuste odstranit parametr t. Dostanete tak rovnici hledané křivky, která je známá již ze střední školy.
Řešení nápovědy 4
\[ x(t)= \hspace{2px}4 \cos \hspace{1px} \left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right) \] \[ y(t)= -4 \sin \hspace{1px} \left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right) \]
Parametru t se jednoduše zbavíme umocněním obou rovnic na druhou a jejich sečtením
\[ x^2= 16 \cos^2 \hspace{1px} \left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right) \] \[ y^2= 16 \sin^2 \hspace{1px} \left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right) \] \[ x^2 + y^2 = 16\underbrace{\left[\cos^2 \hspace{1px} \left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right)+\sin^2 \hspace{1px} \left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right)\right]}_{1} \] \[ x^2 + y^2 = 16. \]
Hmotný bod se tedy pohybuje po kružnici se středem S = [0, 0] a poloměrem 4.
Celkové řešení
ad a)

Složky rychlosti získáme jednoduše derivací
\[ v_{\mathrm{x}}(t) = \frac{\mathrm{d}x(t)}{\mathrm{d}t} = -4 \sin\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right)\frac{2}{3}t = -\frac{8}{3}t\hspace{2px}\sin\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right) \hspace{1px} \] \[ v_{\mathrm{y}}(t) = \frac{\mathrm{d}y(t)}{\mathrm{d}t} = -4 \cos\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right)\frac{2}{3}t = \hspace{2px} -\frac{8}{3 }t\hspace{2px}\cos\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right). \]
Získali jsme tak vektor rychlosti
\[ \vec{v}= \left(-\frac{8}{3}t\hspace{2px}\sin\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right) \hspace{1px},\hspace{2px} -\frac{8}{3 }t\hspace{2px}\cos\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right)\hspace{1px}\right). \]
ad b)

Složky vektoru zrychlení získáme derivací složek rychlosti (derivace součinu)
\[ a_{\mathrm{x}}(t)= \frac{\mathrm{d}v_{\mathrm{x}}(t)}{\mathrm{d}t} = - \frac{8}{3} \sin \left(\frac{1}{3}t^2 + \frac{\pi}{2}\right)\hspace{1px}+\hspace{1px}\left[-\frac{8}{3}t\cos \left(\frac{1}{3}t^2+\frac{\pi}{2}\right)\frac{2}{3}t \right] = \] \[ \hspace{30px} = - \frac{8}{3} \left[ \sin \left(\frac{1}{3}t^2 + \frac{\pi}{2}\right) + \frac{2}{3}t^2 \cos \left(\frac{1}{3}t^2+\frac{\pi}{2}\right)\right] \] \[ a_{\mathrm{y}}(t)= \frac{\mathrm{d}v_{\mathrm{y}}(t)}{\mathrm{d}t} = - \frac{8}{3} \cos \left(\frac{1}{3}t^2 + \frac{\pi}{2}\right)\hspace{1px}+\hspace{1px}\frac{8}{3}t\sin \left(\frac{1}{3}t^2+\frac{\pi}{2}\right)\frac{2}{3}t = \] \[ \hspace{30px}= - \frac{8}{3} \left[ \cos \left(\frac{1}{3}t^2 + \frac{\pi}{2}\right) - \frac{2}{3}t^2 \sin \left(\frac{1}{3}t^2+\frac{\pi}{2}\right)\right]. \]
Získali jsme tak složky vektoru zrychlení \[ \vec{a}= (a_{\mathrm{x}},\hspace{1px}a_{\mathrm{y}}). \]

ad c)

Velikost vektoru rychlosti získáme následovně (vycházíme přitom z Pythagorovy věty - viz obrázek):

\[ \left | \vec{v} \right| = \sqrt{v_{\mathrm{x}}^2+v_{\mathrm{y}}^2} \] \[ \left | \vec{v} \right|=\sqrt{\frac{64}{9}t^2\sin^2 \left(\frac{1}{3}t^2+\frac{\pi}{2}\right) + \frac{64}{9}t^2\cos^2 \left(\frac{1}{3}t^2+\frac{\pi}{2}\right)} \] \[ \left | \vec{v} \right|= \sqrt{\frac{64}{9}t^2 \underbrace{\left[\sin^2 \left(\frac{1}{3}t^2+\frac{\pi}{2}\right)+ \cos^2 \left(\frac{1}{3}t^2+\frac{\pi}{2}\right)\right]}_1} \] \[ \left | \vec{v} \right|= \frac{8}{3}t. \]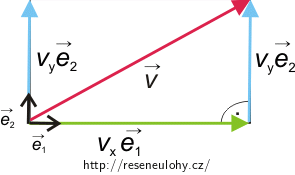
Tečnou složku zrychlení dostaneme derivací velikosti rychlosti podle času:
\[ a_{\mathrm{t}}= \frac{d\left|\vec{v}\right|}{dt}= \frac{8}{3}. \]
ad d)
\[ x(t)= \hspace{2px}4 \cos \hspace{1px} \left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right) \] \[ y(t)= -4 \sin \hspace{1px} \left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right) \]
Parametru t se jednoduše zbavíme umocněním obou rovnic na druhou a jejich sečtením
\[ x^2= 16 \cos^2 \hspace{1px} \left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right) \] \[ y^2= 16 \sin^2 \hspace{1px} \left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right) \] \[ x^2 + y^2 = 16\underbrace{\left[\cos^2 \hspace{1px} \left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right)+\sin^2 \hspace{1px} \left( {\frac{1}{3}t^2 + \frac{\pi}{2}}\right) \right]}_{1} \] \[ x^2 + y^2 = 16. \]
Hmotný bod se tedy pohybuje po kružnici se středem S = [0, 0] a poloměrem 4.
Odpověď
a) Složky vektoru rychlosti jsou
\[ v_{\mathrm{x}}(t) = -\frac{8}{3}t \sin\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right) \] \[ v_{\mathrm{y}}(t) = - \frac{8}{3}t \cos\left(\frac{1}{3}t^2 + \frac{\pi}{2}\right) \]
b) Složky vektoru zrychlení jsou
\[ a_{\mathrm{x}}(t)= - \frac{8}{3} \left[ \sin \left(\frac{1}{3}t^2 + \frac{\pi}{2}\right) + \frac{2}{3}t^2 \cos\left(\frac{1}{3}t^2+\frac{\pi}{2}\right)\right] \] \[ a_{\mathrm{y}}(t)= - \frac{8}{3} \left[\cos \left(\frac{1}{3}t^2 + \frac{\pi}{2}\right) - \frac{2}{3}t^2 \sin\left(\frac{1}{3}t^2+\frac{\pi}{2}\right)\right] \]
c) Velikost vektoru rychlosti je
\[ \left | \vec{v} \right|= \frac{8}{3}t \]
Pro tečnou složku zrychlení platí
\[ a_{\mathrm{t}} = \frac{8}{3} \]
d) Hmotný bod se pohybuje po kružnici se středem S = [0, 0] a poloměrem 4.