Poloha těžiště polokoule
Úloha číslo: 1013
Určete polohu těžiště homogenní polokoule.
Nápověda 1
Úlohou je určit polohu těžiště polokoule.
Nejdřív si zkuste nakreslit kartézskou soustavu souřadnic a vhodně do ní umístěte polokouli.
Poté si zkuste rozmyslet, pomocí jakého vzorce polohu těžiště vypočítáte (vzorec z mechaniky).
Nápověda 2
Ve vzorci se vyskytují dva objemové integrály.
Zkuste si rozmyslet, jaké souřadnice bude mít těžiště polokoule, která je vhodně umístěná do soustavy souřadnic. Využijte při tom homogenitu a symetrii polokoule. Určením některých souřadnic těžiště se integrál v čitateli značně zjednoduší.
Nápověda 3
Nyní si zkuste rozmyslet, jak bude integrace probíhat. Zkuste si polokouli vhodně „rozsekat“. Odkud kam budete integrovat?
Nápověda 4
Nyní je potřeba dosadit do vzorce pro polohu těžiště.
Vyjádřete poloměr r pomocí veličiny R a proměnné z. Pomozte si při tom obrázkem a využijte Pythagorovu větu.
Nezapomeňte, že element dV se zjednoduší, protože jsme využili symetrie koule. Platí
\[\mathrm{d}V = S \mathrm{d}z .\]Obsah kruhu S o poloměru r už jednoduše vyjádříte.
Celkové řešení
Nakreslili jsme si kartézskou soustavu souřadnic a polokouli jsme do ní umístili tak, aby se střed její podstavy nacházel v počátku soustavy (viz obrázek níže). Poloměr polokoule jsme označili R.
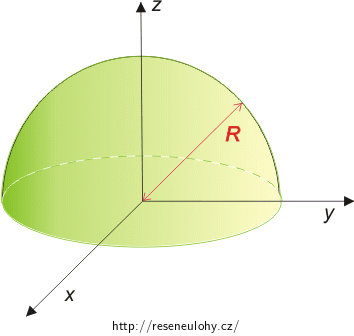
Polohu těžiště vypočítáme pomocí vzorce
\[ \vec{r_{\mathrm{T}}} = \frac{\int_{V}\rho \vec{r} \mathrm{d}V}{\int_{V}\rho \mathrm{d}V} \hspace{3px}, \]kde ρ je hustota polokoule.
je hustota polokoule.Víme, že polokoule je homogenní, má tedy konstantní hustotu ve všech místech objemu. Proto není důvod, aby byla poloha těžiště vychýlena z osy z ve směru osy x nebo y.
Těžiště bude mít proto nenulovou jenom souřadnici z, bude se tedy nacházet v bodě T = [0, 0, zT]. Budeme tedy počítat jen souřadnici zT.
Polokouli si „rozsekáme“ na „válce“ o poloměru r a elementární výšce dz (viz obrázek níže). Poloměr r se bude měnit v závislosti na souřadnici z.
Poznámka: Slovo „válec“ je uvedeno v uvozovkách proto, že se ve skutečnosti jedná o kulový pás o velmi malé výšce (dále uvedeno bez uvozovek).
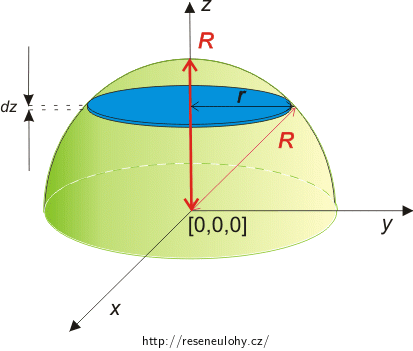
Integrace bude tedy probíhat proměnnou z od 0 do R.
Z obrázku je zřejmé, že pro poloměr r platí
\[ r^2 = R^2 - z^2 . \]Ještě je nutné vyjádřit element dV. Po dosazení za S dostáváme
\[ \mathrm{d}V = S \mathrm{d}z = \pi r^2 \mathrm{d}z= \pi (R^2 - z^2) \mathrm{d}z . \]Víme, že těžiště má nenulovou jenom souřadnici z. Pro polohu těžiště proto dostáváme
\[ z_{\mathrm{T}} = \frac{\int_{0}^{R}\rho z \pi (R^2 - z^2)\mathrm{d}z}{\int_{V}\rho \mathrm{d}V}. \]Využijeme linearity integrování (tj. konstanty dáme před integrál)
\[ z_{\mathrm{T}} = \frac{\pi\rho\int_{0}^{R} z (R^2 - z^2)\mathrm{d}z}{\rho\int_{V} \mathrm{d}V} = \frac{\pi\int_{0}^{R} (zR^2 - z^3)\mathrm{d}z}{\int_{V} \mathrm{d}V} = \frac{\pi \left[ \frac{z^2}{2} R^2 - \frac{z^4}{4}\right]_0^R}{V} = \frac{\pi \left(\frac{R^4}{2}-\frac{R^4}{4}\right)}{V} . \]Po dosazení za objem polokoule V dostáváme
\[ z_{\mathrm{T}} = \frac{\pi \left(\frac{R^4}{2}-\frac{R^4}{4}\right)}{\frac{2}{3}\pi R^3} = \frac{3}{8}R . \]Odpověď
Těžiště homogenní polokoule se nachází na ose symetrie ve 3/8 jejího poloměru nad podstavou polokoule.

