Délka asteroidy
Úloha číslo: 2095
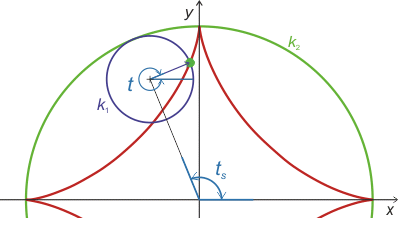
Asteroida (na obrázku červeně) je křivka, kterou opíše jeden bod kružnice k1 o poloměru r1, která se bez prokluzu valí po vnitřní straně větší kružnice k2 o poloměru a, platí-li a = 4r1. Jedná se o jeden z typů hypocykloidy.
Lze také říci, že je zkonstruována stejně jako cykloida, jen není dráhou valící se kružnice přímka, ale vnitřní strana kružnice o čtyřnásobném poloměru.
Zadána je vzdálenost a, tj. délka jednoho ramene asteroidy.
a) Určete její parametrické vyjádření.
b) Určete její délku.
Nápověda a
Postup pro získání parametrických rovnic asteroidy spočívá v přímých úpravách parametrických rovnic kružnice, dokud nevytvoříme požadovanou křivku.
Poznámka: Máte-li potíže s parametrickými rovnicemi, jejich významem a použitím, podívejte se na úlohu Délka oblouku cykloidy, kde se velmi podrobně odvozují parametrické rovnice kružnice a poté cykloidy.Řešení a
Poznámka: V této části řešení se již předpokládá určitá znalost práce s parametrickými rovnicemi, proto bude odvození rychlé. Nerozumíte-li některým krokům, podívejte se na úlohu Délka oblouku cykloidy, kde se postupuje po menších krocích.
Začneme s parametrickými rovnicemi kružnice, která má střed mimo počátek souřadného systému. Zároveň chceme, aby počáteční bod byl bod kružnice nejvíce vpravo (A(t1)), a aby se zvyšující se hodnotou parametru přibývaly body po směru hodinových ručiček. Tuto kružnici si označíme k1.
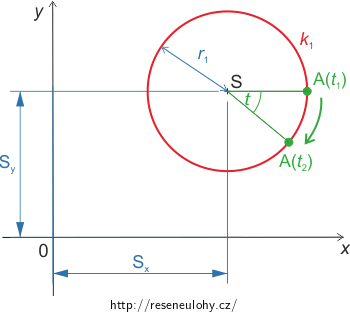
V našem případě tedy budou parametrické rovnice kružnice k1 mít tvar
\[x=S_x+r_1\cos t\] \[y=S_y-r_1\sin t.\tag{1}\]r1 je poloměr kružnice k1, Sx a Sy jsou souřadnice středu této kružnice, t její parametr.
V dalším kroku se pokusíme zajistit, aby se střed kružnice k1 se zvyšujícím se parametrem pohyboval po kružnici, kterou označíme ks.
Poloměr kružnice ks si zatím označíme rs a její parametr ts, umístěna bude ve středu souřadného systému, počáteční bod bude úplně vpravo, s rostoucím parametrem se budou vytvářet body proti směru hodinových ručiček. Máme tedy
\[S_x=r_s \ \cos t_s\] \[S_y=r_s \ \sin t_s\,,\]kde Sx a Sy jsou souřadnice středu kružnice k1 a zároveň souřadnice bodů kružnice ks.
Dále musíme určit, jakou hodnotu by měl mít poloměr rs. V úvodu úlohy je řečeno, že se malá kružnice má valit po vnitřní straně větší kružnice o čtyřnásobném poloměru. Střed kružnice k1 bude tedy vždy o hodnotu poloměru r1 blíže středu souřadného systému, než poloměr kružnice k2.
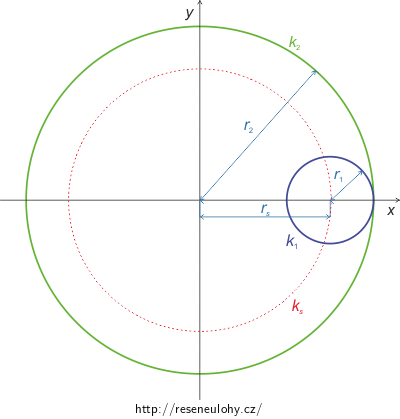
Platí tedy
\[r_2=4r_1\] \[r_s=r_2-r_1=4r_1-r_1=3r_1\] \[r_1=\frac{1}{3}r_s.\]Tím jsme vyjádřili poloměr r1 pomocí poloměru rs, budeme tedy moci sjednotit naše rovnice, aby obsahovaly pouze jeden z těchto poloměrů. Dále bude zapotřebí sjednotit parametry t a ts.
Jak je vidět z následujícího obrázku, je jisté, že za parametry ts a t nelze dosazovat stejné hodnoty.
Musíme tedy zjistit, v jakém poměru vůči sobě musí tyto parametry být. K tomu nám postačí úvaha: představte si, jak je vytvářen bod v nejvyšším bodě asteroidy. Úhel t musí být \(\frac{3\pi}{2}\). Úhel ts v tomto případě bude jen \(\frac{\pi}{2}\). Aby toto platilo, stačí zavést
\[t_s=\frac{t}{3}.\tag{2}\]Poznámka 1: Zkuste porovnat i úhly v dalších polohách. (Zkuste například bod asteroidy úplně nalevo, dejte si ale pozor, jaký úhel opíše t - nebude to pouze π!)
Poznámka 2: Další možností je porovnání obvodů kružnic ks a k1. Protože se kružnice musí valit bez prokluzu, z porovnání poloměrů je možné zjistit, kolikrát se malá kružnice otočí, než se vrátí do výchozí pozice. Tento počet nám udá, kolikrát musí být ts menší, než t.
Z tohoto výsledku se dá také snadno určit, jakých hodnot bude parametr t nabývat. Aby byla asteroida celá, musel původní úhel ts nabývat hodnot od 0 do 2π. Stačí do naší převodní rovnice (2) dosadit za ts hodnotu 2π a zjistíme, že t bude nabývat hodnot od 0 do 6π (kružnice k1 se tedy musí otočit přesně 3×, aby vytvořila celou asteroidu a vrátila se do výchozí pozice).
Nyní můžeme upravit parametrické rovnice pro kružnici k1:
\[x=S_x+\frac{1}{3} r_s \cos ( 3t_s )\] \[y=S_y-\frac{1}{3} r_s \sin ( 3t_s )\]a dosadit do nich parametrické rovnice kružnice ks (1):
\[x=r_s \cos t_s+\frac{1}{3} r_s \cos ( 3t_s )\] \[y=r_s \sin t_s-\frac{1}{3} r_s \sin ( 3t_s ).\]Nyní vytkneme \(\frac{1}{3} r_s\):
\[x=\frac{1}{3} r_s [3\cos t_s+\cos ( 3t_s )]\] \[y=\frac{1}{3} r_s [3\sin t_s-\sin ( 3t_s )].\]V tomto tvaru můžeme na výraz uvnitř hranatých závorek použít vzorce trigonometrických funkcí trojnásobných úhlů:
\[\sin(3\alpha)=3\sin\alpha-4\sin^3\alpha\] \[\cos(3\alpha)=4\cos^3\alpha-3\cos\alpha.\]Tím získáme:
\[x=\frac{4}{3}r_s \cos^3 (t_s)\] \[y=\frac{4}{3}r_s \sin^3 (t_s).\]To je již přijatelně jednoduchý tvar, ale můžeme najít ještě další zjednodušení. Za prvé vidíme, že člen \(\frac{4}{3}r_s\) je vlastně naším známým rozměrem a (poloměr vnější kružnice ze zadání úlohy). Navíc si pro další použití přeznačíme ts na t. Výsledné rovnice tedy budou mít tvar:
\[x=a \cos^3 t\] \[y=a \sin^3 t,\]kde parametr \(t \in \lt 0;2\pi).\)
Nápověda b
Neznáte-li vzorec pro délku obecné křivky zadané parametrickými rovnicemi, podívejte se na úlohu Délka oblouku cykloidy, kde je tento vzorec odvozen v „Řešení nápovědy b“.
Během určování délky asteroidy se možná dostanete k řešení, kdy vám vyjde, že délka asteroidy je nulová. Zamyslete se, jak se můžete tomuto výsledku vyhnout. Především se podívejte, jaký výraz vám tento očividně špatný výsledek způsobuje, a využijte symetrie asteroidy.
Řešení b
K této části je zapotřebí znát parametrické rovnice asteroidy a vzorec pro délku obecné křivky. Posledním krokem bude spojit tyto dvě znalosti dohromady.
Parametrické rovnice asteroidy:
\[x=a \cos^3 t\] \[y=a \sin^3 t.\]Vzorec pro délku obecné křivky ve dvourozměrném prostoru:
\[S_\Gamma= \int^a_b \sqrt{\left( \frac{\mathrm{d}x}{\mathrm{d}t} \right)^2 + \left( \frac{\mathrm{d}y}{\mathrm{d}t} \right)^2}\mathrm{d}t. \]Za proměnné x a y ve vzorci pro délku křivky je zapotřebí dosadit z parametrických rovnic. Protože se obě proměnné vyskytují v derivacích, je výhodné si tyto derivace nejprve připravit:
\[\frac{\mathrm{d}x}{\mathrm{d}t}=-3a\ \cos^2 t\ \sin t\] \[\frac{\mathrm{d}x}{\mathrm{d}t}=3a\ \sin^2 t\ \cos t.\]Po dosazení derivací do vzorce pro délku křivky získáme:
\[S_\Gamma= \int^{2\pi}_0 {\sqrt{9a^2 \cos^4 t \sin^2 t + 9a^2 \sin^4 t \cos^2 t}} \ \mathrm{d}t.\]A dále upravujeme. Nejprve se „zbavíme“ členu 9a2, který lze vytknout před odmocninu jako 3a. A protože jde o konstantu, můžeme 3a vytknout až před integrál.
\[S_\Gamma= 3a \int^{2\pi}_0 {\sqrt{ \cos^4 t \sin^2 t + \sin^4 t \cos^2 t}} \ \mathrm{d}t\]Podobně můžeme z odmocniny vytknout cos2t a sin2t:
\[S_\Gamma= 3a \int^{2\pi}_0 \cos t \sin t {\sqrt{ \cos^2 t + \sin^2 t }} \ \mathrm{d}t,\]čímž pod odmocninou získáme známý goniometrický vzorec pro „goniometrickou jedničku“.
\[S_\Gamma= 3a \int^{2\pi}_0 \cos t \sin t \ \mathrm{d}t\]V tomto tvaru můžeme integrál řešit například substitucí:
\[ u= \sin t\] \[\mathrm d u= \cos t \ \mathrm d t.\]Pokud se však pokusíme vypočítat integrační meze této substituce, zjistíme, že obě vyjdou rovny nule (vysvětlení viz Poznámka na konci této sekce). To je samozřejmě chybný výsledek, délka asteroidy je zcela určitě nenulová při nenulovém a. Musíme tedy zajistit, aby meze nevyšly stejné. Dosáhnout toho lze jednoduchou úvahou: asteroida je symetrická podle dvou os. Jinými slovy, lze ji rozdělit na čtyři stejné části, které jsou pouze vzájemně otočené a posunuté. Z toho je tedy patrné, že stačí vypočíst délku pouze jedné čtvrtiny a výsledná délka bude čtyřnásobkem takového výsledku.
Náš integrál zůstane tedy stejný, jen před substitucí změníme integrační meze, abychom počítali délku jedné čtvrtiny asteroidy.
\[S_{\frac{1}{4}}= 3a \int^{\frac{\pi}{2}}_0 \cos t \sin t \ \mathrm{d}t\] \[ u= \sin t\] \[\mathrm d u= \cos t \ \mathrm d t\]Integrační meze:
\[u_1=0\] \[u_2=1\]Po substituci získáme:
\[S_{\frac{1}{4}}= 3a \int^{1}_0 u \ \mathrm{d}u.\]A takovýto integrál již není těžké integrovat:
\[S_{\frac{1}{4}}= 3a \left[ \frac{1}{2} u^2 \right]_0^1=\frac{3}{2}a.\]Tento výsledek je tedy délka jedné čtvrtiny asteroidy. Stačí vynásobit čtyřmi a získáme délku celé asteroidy:
\[S_\Gamma=6a.\]Odpověď a
Parametrické vyjádření ateroidy:
\[x=a \cos^3 t\] \[y=a \sin^3 t,\]kde \(t \in <0;2\pi).\)
Odpověď b
Délka asteroidy:
\[S_\Gamma=6a.\]