Dělo střílející z kopce
Úloha číslo: 1146
Na vrcholu kopce, který svírá s vodorovnou rovinou úhel 30°, je umístěno dělo, ze kterého je vystřeleno. V okamžiku výstřelu svírá hlaveň s vodorovnou rovinou určitý elevační úhel a je namířena tak, že vystřelená střela dopadne na dolní část kopce ve vzdálenosti 6 km od místa výstřelu. Určete minimální velikost rychlosti, se kterou střela opustila hlaveň děla, a hodnotu elevačního úhlu hlavně při výstřelu. Odporové síly zanedbejte.
Zápis
φ = 30° úhel mezi svahem kopce a vodorovnou rovinou d = 6 km vzdálenost, do které dopadne střela vmin = ? minimální rychlost střely při opuštění hlavně α0 = ? elevační úhel příslušející rychlosti vmin Popis metody
Naším cílem bude najít velikost počáteční rychlosti jako funkci elevačního úhlu α: v0 = v0(α). Pomocí diferenciálního počtu pak nalezneme takový elevační úhel α0, pro který nabývá tato funkce (= počáteční rychlost) minima. Jeho dosazením do v0 = v0(α) získáme požadovanou minimální velikost rychlosti.
Nápověda 1
Než začnete úlohu řešit, nakreslete si obrázek, který situaci (včetně místa dopadu) popisuje. Vhodným způsobem do něj pak zaveďte souřadný systém a v něm vyjádřete ze zadaných veličin souřadnice bodu dopadu střely. Věnujte tomuto úkolu pozornost, obrázek je zde základem dalšího úspěšného řešení!
Nápověda 2
Rozmyslete si, jaký druh pohybu bude střela po opuštění hlavně vykonávat. Pro tento pohyb napište časový vývoj složek rychlosti vx(t), vy(t) a časový vývoj souřadnic střely x(t), y(t).
Nápověda 3
Znáte souřadnice bodu dopadu D, umíte tedy vyjádřit dobu letu střely.
Nápověda 4
Naším cílem popsaným v úvodu úlohy je dostat se ke vztahu v0 = v0(α). Dosaďte tedy dobu letu získanou ve vztahu (8) do rovnice (7) a vyjádřete počáteční rychlost v0 jako funkci elevačního úhlu α.Nápověda 5
Jak nyní určit elevační úhel, pro který funkce ze vztahu (10) nabývá minimální hodnoty? Pomohlo by nám derivování funkce? Jak? Proveďte výpočet a najděte takový elevační úhel α0.
Nápověda 6
Určili jsme elevační úhel, při kterém bude počáteční rychlost minimální, zbývá dopočítat tuto počáteční rychlost vmin. Který vztah je výhodné použít?
Celkové řešení
Situaci včetně zavedení souřadného systému ukazuje obrázek níže:
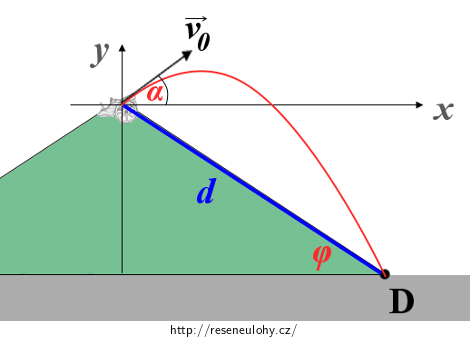
Červeně je znázorněna trajektorie střely. Počátek souřadného systému je umístěn na vrchol kopce, písmenem D je označeno místo dopadu střely. Pomocí goniometrických funkcí snadno určíme souřadnice bodu D:
\[D\,=\,[x_\mathrm{D}, y_\mathrm{D}]\,=\,[d\cos{\varphi}, -d\sin{\varphi}].\tag{1}\]Po opuštění hlavně koná střela složený pohyb, který označujeme jako šikmý vrh (tento pohyb je složen z rovnoměrných přímočarých pohybů ve směru souřadných os a volného pádu). Pro složky rychlosti ve směrech souřadných os při takovémto pohybu s počáteční rychlostí v0 a elevačním úhlem α platí:
\[v_\mathrm{x}(t)\,=\,v_0\cos{\alpha},\tag{2}\] \[v_\mathrm{y}(t)\,=\,v_0\sin{\alpha}\,-\,gt,\tag{3}\]kde g je tíhové zrychlení. Časový vývoj souřadnic střely můžeme získat buď ze vztahů pro dráhu rovnoměrného, resp. rovnoměrně zrychleného pohybu, nebo jednoduchou integrací vztahů (2) a (3). Oběma postupy dostáváme:
\[x(t)\,=\,v_0t\cos{\alpha},\tag{4}\] \[y(t)\,=\,v_0t\sin{\alpha}\,-\,\frac{1}{2}gt^2.\tag{5}\]Souřadnice bodu D jsme již vyjádřili v úvodu úlohy, jejich dosazením do vztahů (4) a (5) dostáváme pro dobu letu tD:
\[d\cos{\varphi}\,=\,v_0t_\mathrm{D}\cos{\alpha},\tag{6}\] \[-d\sin{\varphi}\,=\,v_0t_\mathrm{D}\sin{\alpha}\,-\,\frac{1}{2}gt_\mathrm{D}^2.\tag{7}\]Dobu letu tD vyjádříme nejsnadněji ze vztahu (6):
\[t_\mathrm{D}\,=\,\frac{d\cos{\varphi}}{ v_0\cos{\alpha}}.\tag{8}\]Získanou dobu letu tD dosadíme ze vztahu (8) do rovnice (7) a vyjádříme odtud hledanou závislost v0 = v0(α):
\[-d\sin{\varphi}\,=\,v_0(\frac{d\cos{\varphi}}{v_0\cos{\alpha}})\sin{\alpha}\,-\,\frac{1}{2}g(\frac{d\cos{\varphi}}{v_0\cos{\alpha}})^2.\tag{9}\]Úpravami dostáváme:
\[-2dv_0^2\sin{\varphi}\cos^2{\alpha}\,=\,2dv_0^2\cos{\varphi}\cos{\alpha}\sin{\alpha}\,-\,gd^2\cos^2{\varphi},\] \[gd\cos^2{\varphi}\,=\,v_0^2(2\sin{\varphi}\cos^2{\alpha}\,+\,\sin{2\alpha}\cos{\varphi}),\] \[v_0\,=\, v_0(\alpha)\,=\,\sqrt{\frac{dg\cos^2{\varphi}}{2\sin{\varphi}\cos^2{\alpha}\,+\,\sin{2\alpha}\cos{\varphi}}}.\tag{10}\]Funkci ze vztahu (10) zderivujeme podle proměnné α a najdeme takové α0, pro které bude hodnota první derivace nulová. V takovém bodě podle znalostí z diferenciálního počtu nabývá funkce ze vztahu (10) svého lokálního extrému – v tomto případě minima. (Důkaz, že jde skutečně o minimum, zde ukazovat nebudeme, lze jej provést pomocí grafu příslušné funkce nebo dalším derivováním.)
Derivováním vztahu (10) tedy dostáváme:
\[\frac{dv_0}{d{\alpha}}\,=\,(\sqrt{dg\cos^2{\varphi}})(-\frac{1}{2})(2\cos^2{\alpha}\sin{\varphi}\,+\,\sin{2\alpha}\cos{\varphi})^{-\frac{3}{2}}{\cdot}\] \[{\cdot}(4\cos{\alpha}(-\sin{\alpha})\sin{\varphi}\,+\,2\cos{2\alpha}\cos{\varphi}),\tag{11}\] \[\frac{dv_0}{d{\alpha}}\,=\,-\frac{1}{2}\sqrt{\frac{dg\cos^2{\varphi}}{(2\cos^2{\alpha}\sin{\varphi}\,+\,\sin{2\alpha}\cos{\varphi})^3}}{\cdot}\] \[{\cdot}(-4\cos{\alpha}\sin{\alpha}\sin{\varphi}\,+\,2\cos{2\alpha}\cos{\varphi}).\tag{12}\]Hledáme takové α0, pro které je derivace nulová, je tedy patrné, že vždy kladnou odmocninu nemusíme vyšetřovat:
\[\frac{dv_0}{d{\alpha}}\,=\,0\,\Leftrightarrow\,2\cos{\alpha_0}\sin{\alpha_0}\sin{\varphi}\,=\,\cos{(2\alpha_0)}\cos{\varphi}.\tag{13}\]S použitím vztahu pro dvojnásobný úhel dostáváme:
\[\sin{2\alpha_0}\,=\,\cos{2\alpha_0}\frac{\cos{\varphi}}{\sin{\varphi}},\tag{14}\] \[\tan{2\alpha_0}\,=\,\cot{\varphi}.\tag{15}\]Číselně:
\[\tan{2\alpha_0}\,=\,\cot{30°}\,=\,\sqrt{3}\,\Rightarrow\,2\alpha_0\,=\,60°\,\Rightarrow\,\alpha_0\,=\,30°.\]Elevační úhel, pro který je počáteční rychlost minimální, je 30°.
Vztah pro počáteční rychlost v závislosti na elevačním úhlu jsme odvodili ve vztahu (10), dosadíme do něj tedy získaný úhel α0. Číselně:
\[v_\mathrm{min}\,=\,v_0(\alpha_0)\,=\,\sqrt{\frac{6\,000{\cdot}10{\cdot}(\cos{30°})^2}{2\sin{30°}(\cos{30°})^2\,+\,\sin{60°}\cos{30°}}}\,\mathrm{m}\cdot\mathrm{s}^{-1},\] \[v_\mathrm{min}\,=\,\sqrt{30000}\,\mathrm{m}\cdot\mathrm{s}^{-1}\,\dot=\,173\,\mathrm{m}\cdot\mathrm{s}^{-1}.\]Minimální počáteční rychlost střely byla přibližně 173 m·s−1.
Odpověď
Minimální rychlost, se kterou musí střela opustit hlaveň děla, je přibližně 173 m·s−1, elevační úhel je v takovém případě 30°.





