Pád s odporem vzduchu
Úloha číslo: 1015
Uvažujte pád hmotného bodu v homogenním tíhovém poli Země, kde působí vzduch odporovou silou, jejiž velikost je přímo úměrná první mocnině velikosti rychlosti hmotného bodu.
Sestavte pohybovou rovnici a určete závislost velikosti rychlosti hmotného bodu na čase, když víte, že v čase t = 0 byla velikost počáteční rychlosti hmotného bodu nulová.
Poznámka: Vektory jsou v úloze značeny tučně.
Nápověda 1
Úlohou je sestavit pohybovou rovnici pro pád hmotného bodu za působení odporové síly, jejiž velikost je přímo úměrná první mocnině velikosti rychlosti hmotného bodu.
Zkuste si nejdřív nakreslit danou situaci, tj. síly, které působí na hmotný bod.
Nápověda 2
Zamyslete se, jak bude vypadat pohybová rovnice pro pád hmotného bodu za působení odporové síly, jejiž velikost je přímo úměrná první mocnině velikosti rychlosti. Pomůže vám k tomu obrázek uvedený v sekci Řešení nápovědy 1.
Nápověda 3
Zamyslete se, jakého typu je daná diferenciální rovnice a jak se řeší.
V diferenciální rovnici se vyskytuje první derivace rychlosti. Rozmyslete si, jakou úpravou byste se derivace „zbavili“.
Nápověda 4
Ještě zbývá určit konstantu z0. K jejímu výpočtu zkuste použít počáteční podmínku uvedenou v zadání.
Celkové řešení
Při pádu v tíhovém poli Země působí na hmotný bod tíhová síla \( \vec {F_G}\). Ze zadání víme, že odporová síla působí proti směru pohybu, tj. v našem případě proti tíhové síle \(\vec {F_o}\). Výslednou sílu jsme označili \(\vec F\).
Situace je znázorněná na obrázku níže.
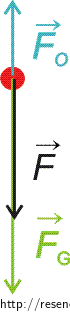
Víme, že odporová síla působí proti síle tíhové. Pro výslednou sílu \(\vec F\) platí
\[ \vec{F} = \vec{F}_{\mathrm{G}} + \vec{F}_{\mathrm{o}} . \]Pro velikost výsledné síly platí
\[ F = F_{\mathrm {G}} - F_{\mathrm{o}} . \]Dále víme, že velikost odporové síly je přímo úměrná první mocnině velikosti rychlosti hmotného bodu, pro její velikost proto platí
\[ F_{\mathrm{o}} = kv , \]kde k > 0 je konstanta.
Z 2. Newtonova zákona dostáváme pohybovou rovnici, která vypadá následovně:
\[ m \frac{\mathrm{d}v}{\mathrm{d}t} = mg - kv . \]Poznámka: Jedná se o pohyb v přímce (ve svislém směru), proto vystačíme s rovnicí pro jedinou souřadnici rychlosti v.
Uvedená rovnice je lineární diferenciální rovnice prvního řádu s konstantními koeficienty.
Po vydělení rovnice hmotností m a následnou separací proměnných dostáváme
\[ \frac{\mathrm{d}v}{\mathrm{d}t} = g - \frac{k}{m}v \] \[ \frac{\mathrm{d}v}{g - \frac{k}{m}v} = \mathrm{d}t . \]Zintegrujeme obě strany rovnice
\[ \int \frac{\mathrm{d}v}{g - \frac{k}{m}v} =\int \mathrm{d}t . \]Zavedením substituce
\[ g - \frac{k}{m}v = z \hspace{20px} \Rightarrow \hspace{20px} \mathrm{d}v = - \frac{m}{k}\mathrm{d}z , \]Poznámka: Nenechte se zmást, z není kartézská souřadnice polohy, ale náhodně zvolené označení.
dostáváme
\[ -\frac{m}{k} \int \frac{\mathrm{d}z}{z} = \int \mathrm{d}t . \] \[ -\frac{m}{k}\hspace{1px} \ln \left({\frac{z}{z_{\mathrm{0}}}}\right) = t . \]Poznámka: V argumentu logaritmu jsme z vydělili konstantou z0, aby se v argumentu přirozeného logaritmu vyskytovala bezrozměrná veličina.
Vynásobením obou stran rovnice výrazem \[-\frac{k}{m}\] a následnou aplikací exponenciály dostáváme
\[ \ln \left({\frac{z}{z_{\mathrm{0}}}}\right) = -\frac{k}{m}t \] \[ \frac{z}{z_{\mathrm{0}}} = e^{-\frac{k}{m}t} \] \[ z = z_{\mathrm{0}} e^{-\frac{k}{m}t} . \]Nyní se vrátíme k substituci a provedeme několik jednoduchých úprav
\[ g - \frac{k}{m}v = z_{\mathrm{0}} e^{-\frac{k}{m}t} \] \[ - \frac{k}{m}v = z_{\mathrm{0}} e^{-\frac{k}{m}t} - g \] \[ v = - \frac{m}{k} \left(z_{\mathrm{0}} e^{-\frac{k}{m}t} - g\right). \]Pro časovou závislost rychlosti hmotného bodu při pádu za působení odporové síly, jejiž velikost je přímo úměrná první mocnině rychlosti platí :
\[ v = \frac{m}{k} \left(g - z_{\mathrm{0}}e^{-\frac{k}{m}t}\right) . \tag{1}\]Zbývá nám ještě určit konstantu z0, k čemuž využijeme počáteční podmínku. Víme, že v čase t = 0 byla velikost rychlosti nulová. Po dosazení do rovnice (1) dostáváme
\[ 0 = \frac{m}{k} \left(g - z_{\mathrm{0}} e^0\right) \] \[ 0 = \frac{m}{k}\left( g - z_{\mathrm{0}}\right) \] \[ z_{\mathrm{0}} = g. \]Po dosazení konstanty z0 do závislosti (1) dostáváme
\[ v = \frac{m}{k} \left(g - g e^{-\frac{k}{m}t}\right) . \]Výsledná závislost tedy vypadá následovně:
\[ v = \frac{m}{k}g\left(1 - e^{-\frac{k}{m}t}\right) . \]Odpověď
Závislost rychlosti hmotného bodu na čase při pádu v tíhovém poli Země za působení zadané odporové síly je popsána rovnicí
\[ v = \frac{m}{k}g\left(1 - e^{-\frac{k}{m}t}\right). \]

