Těžiště drátu ve tvaru půlkruhu

Úloha číslo: 1116

Určete polohu těžiště tenkého homogenního drátu hmotnosti m ohnutého do tvaru půlkruhu o poloměru R.

Nápověda 1
Zamyslete se nad tím, co vlastně znamená úkol „určete polohu těžiště“. Co má být výstupem úlohy, co vlastně určujete?
Řešení nápovědy 1
Určit polohu těžiště znamená určit souřadnice těžiště v nějakém vhodně zvoleném souřadném systému. Výstupem jsou tedy tři souřadnice těžiště T: x_T, y_T, z_T.
Nápověda 2
Nakreslete si příslušný půlkruh do souřadného systému. Lze jej tam umístit tak, aby se další výpočty zjednodušily? (Nebo ještě jinak – musíme opravdu počítat x-ovou, y-ovou i z-ovou souřadnici? Nelze zvolit souřadný systém tak, aby některé souřadnice byly zřejmé?)
Řešení nápovědy 2
Vhodné zvolení souřadného systému, ve kterém bude další výpočet probíhat, může vypadat například takto:

Představte si, že položíme půlkruhový drát na vodorovný stůl. Při pohledu shora vidíme v podstatě půlkružnici (obr. 1).

Osu z zvolíme svisle vzhůru (v obrázku tedy míří ven z obrazovky).

Osu y zvolíme tak, aby při pohledu shora půlila viděnou půlkružnici na dvě čtvrtkružnice.

Osa x je pak kolmá na obě osy předchozí.

Drát (tenký) leží v rovině xy. Souřadnice z těžiště je tedy nulová:
\[z_\mathrm{T}\,=\,0.\]
Z obrázku je patrné, že také x-ová souřadnice těžiště je nulová:
\[x_\mathrm{T}\,=\,0.\]
(Objekt je totiž symetrický podle osy y, jeho těžiště tedy musí ležet na této ose.) Zbývá nám tedy určit y-ovou souřadnici těžiště.
Nápověda 3
Jak je obecně definován vztah pro výpočet polohového vektoru r_T, který určuje polohu těžiště?
Řešení nápovědy 3
Polohový vektor r_T určující polohu těžiště daného objektu lze určit jako:
\[\vec{r}_\mathrm{T}\,=\,\frac{\int{\vec{r}}dm}{{\int}dm}.\tag{1}\]
Nápověda 4
Drát je podle zadání úlohy homogenní. Využijte toho k tomu, abyste od hmotnostních elementů ve vztahu (1) přešli k elementům délkovým.
Řešení nápovědy 4
Element hmotnosti dm lze pro homogenní drát rozepsat jako součin:

\[dm\,=\,{\rho}dl,\]

kde ρ je délková hustota materiálu a dl je element délky. Pak platí:
\[\vec{r}_\mathrm{T}\,=\,\frac{{\rho}\int{\vec{r}}dl}{{\rho}{\int}dl}\,=\,\frac{\int{\vec{r}}dl}{{\int}dl}.\]
Výraz ve jmenovateli představuje vysčítání všech délkových elementů, které drát tvoří – dostáváme zde tedy délku drátu l:
\[\vec{r}_\mathrm{T}\,=\,\frac{\int{\vec{r}}dl}{l}.\tag{2}\]
Nápověda 5
Jak se změní vztah (2), pokud se budeme (dle počáteční úvahy) zabývat pouze y-ovou souřadnicí těžiště y_T?
Řešení nápovědy 5
Protože souřadnice polohového vektoru r_T se ve vztazích (1) i (2) počítají po složkách, lze jednoduše pro y-ovou souřadnici psát:
\[y_\mathrm{T}\,=\,\frac{\int{y}dl}{l}.\tag{3}\]
Nápověda 6
Počítat dále dle vztahu (3) je v kartézských souřadnicích velmi nepohodlné. Vyznačte si do obrázku krátký délkový element dl, jemu odpovídající souřadnici y a úhel φ odečítaný od osy x proti směru hodinových ručiček. Vyjádřete kartézskou souřadnici y pomocí poloměru půlkruhu R a úhlu φ. Také délkový element dl zapište pomocí jemu odpovídajícímu úhlu dφ a poloměru R (pomozte si obrázkem).
Řešení nápovědy 6

Pro konkrétní φ platí:
\[\sin{\varphi}\,=\frac{y}{R}\,\Rightarrow\,y\,=\,R\sin{\varphi}.\tag{5}\]
Dle obr. 2 je také patrné, že platí:
\[dl\,=\,Rd\varphi.\tag{4}\]
Dosazením do vztahu (3) dostáváme:
\[y_\mathrm{T}\,=\,\frac{\int{R\sin{\varphi}Rd\varphi}}{l}.\]
Doplnit můžeme ještě délku půlkruhu, která je l = πR:
\[y_\mathrm{T}\,=\,\frac{\int{R^2\sin{\varphi}d\varphi}}{{\pi}R}\,=\,\frac{R}{\pi}\int{\sin{\varphi}d{\varphi}}.\tag{6}\]
Nápověda 7
V integrálu (6) doplňte příslušné integrační meze a dopočítejte souřadnici těžiště.
Řešení nápovědy 7
Úhel φ se mění v mezích od φ = 0 do φ = π.
\[y_\mathrm{T}\,=\,\frac{R}{\pi}\int_0^{\pi}{\sin{\varphi}d{\varphi}}\,=\,\frac{R}{\pi}[-\cos{\varphi}]_0^{\pi}\,=\,\frac{R}{\pi}(1-(-1))\,=\,\frac{2R}{\pi}\]
Poslední neurčená souřadnice těžiště v námi zvoleném souřadném systému je y_T = 2R/π.
Celkové řešení
Určit polohu těžiště znamená určit souřadnice těžiště v nějakém vhodně zvoleném souřadném systému. Výstupem jsou tedy tři souřadnice těžiště T: x_T, y_T, z_T.

Vhodným zvolením souřadného systému můžeme docílit toho, že některé souřadnice těžiště získáme bez výpočtů. Takové zvolení souřadného systému (ve kterém bude další výpočet probíhat), může vypadat například takto:

Představte si, že položíme půlkruhový drát na vodorovný stůl. Při pohledu shora vidíme v podstatě půlkružnici (obr. 1).

Osu z zvolíme svisle vzhůru (v obrázku tedy míří ven z obrazovky).

Osu y zvolíme tak, aby při pohledu shora půlila viděnou půlkružnici na dvě čtvrtkružnice.

Osa x je pak kolmá na obě osy předchozí.

Drát (tenký) leží v rovině xy. Souřadnice z těžiště je tedy nulová:
\[z_\mathrm{T}\,=\,0.\]
Z obrázku je patrné, že také x-ová souřadnice těžiště je nulová:
\[x_\mathrm{T}\,=\,0.\]
(Objekt je totiž symetrický podle osy y, jeho těžiště tedy musí ležet na této ose.) Zbývá tedy určit y-ovou souřadnici těžiště.

Polohový vektor r_T určující polohu těžiště daného objektu lze určit jako:
\[\vec{r}_\mathrm{T}\,=\,\frac{\int{\vec{r}}dm}{{\int}dm}.\tag{1}\]
Element hmotnosti dm lze pro homogenní drát rozepsat jako součin:

\[dm\,=\,{\rho}dl,\]

kde ρ je délková hustota materiálu a dl je element délky. Pak platí:
\[\vec{r}_\mathrm{T}\,=\,\frac{{\rho}\int{\vec{r}}dl}{{\rho}{\int}dl}\,=\,\frac{\int{\vec{r}}dl}{{\int}dl}.\]
Výraz ve jmenovateli představuje vysčítání všech délkových elementů, které drát tvoří – dostáváme zde tedy délku drátu l:
\[\vec{r}_\mathrm{T}\,=\,\frac{\int{\vec{r}}dl}{l}.\tag{2}\]
Protože souřadnice polohového vektoru r_T se ve vztazích (1) i (2) počítají po složkách, lze jednoduše pro y-ovou souřadnici psát:
\[y_\mathrm{T}\,=\,\frac{\int{y}dl}{l}.\tag{3}\]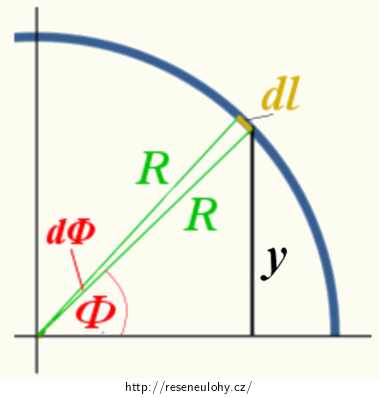

Přejdeme k jiným proměnným. Z obr. 2 je vidět, že pro konkrétní úhel φ platí:
\[\sin{\varphi}\,=\frac{y}{R}\,\Rightarrow\,y\,=\,R\sin{\varphi}.\tag{5}\]
Z obr. 2 je také patrné, že platí:
\[dl\,=\,Rd\varphi.\tag{4}\]
Dosazením do vztahu (3) dostáváme:
\[y_\mathrm{T}\,=\,\frac{\int{R\sin{\varphi}Rd\varphi}}{l}.\]
Doplnit můžeme ještě délku půlkruhu, která je l = πR:
\[y_\mathrm{T}\,=\,\frac{\int{R^2\sin{\varphi}d\varphi}}{{\pi}R}\,=\,\frac{R}{\pi}\int{\sin{\varphi}d{\varphi}}.\tag{6}\]
Doplníme meze pro úhel φ. Ten se mění od φ = 0 do φ = π.
\[y_\mathrm{T}\,=\,\frac{R}{\pi}\int_0^{\pi}{\sin{\varphi}d{\varphi}}\,=\,\frac{R}{\pi}[-\cos{\varphi}]_0^{\pi}\,=\,\frac{R}{\pi}(1-(-1))\,=\,\frac{2R}{\pi}\]
Poslední neurčená souřadnice těžiště v námi zvoleném souřadném systému y_T = 2R/π, ostatní souřadnice jsou nulové.
Odpověď
Souřadnice těžiště v námi zvoleném souřadném systému jsou:
\[x_\mathrm{T}\,=\,0,\] \[y_\mathrm{T}\,=\,\frac{2R}{\pi},\] \[z_\mathrm{T}\,=\,0.\]