Stabilní rovnovážná poloha polokoule se závažím
Úloha číslo: 1030
Najděte stabilní rovnovážnou polohu homogenní polokoule s poloměrem R a hmotností M, na jejímž okraji je napevno umístěné navíc závaží o hmotností m (viz obrázek níže).
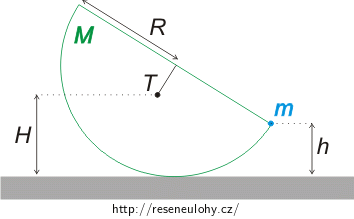
Poznámka 1: Bod T zde označuje těžiště polokoule.
Poznámka 2: Vektory jsou v úloze značeny tučně.
Nápověda 1
Úlohou je najít stabilní rovnovážnou polohu polokoule se závažím.
Zkuste si nejdřív do obrázku nakreslit síly, které působí na polokouli a závaží.
Nápověda 2
Z mechaniky je známo, že těleso má tendenci zaujmout takovou polohu, při které je jeho potenciální energie tíhová minimální.
Poznámka: Potenciální energie tíhová nabývá minima v rovnovážné poloze stálé (stabilní), nikoli vratké.
Zamyslete se, jaká bude potenciální energie tíhová Ep polokoule se závažím. Vyjádřete ji v závislosti na úhlu φ.
Pomozte si obrázkem.
Nápověda 3
Z předchozího už víte, že v rovnovážné poloze stabilní bude mít potenciální energie tíhová extrém (minimum).
Zkuste se zamyslet, jak naleznete extrém funkce Ep.
Nápověda 4
Podmínka \[\frac{\mathrm{d}E_{\mathrm{p}}}{\mathrm{d}\varphi} = 0\] je nutná podmínka extrému, nikoli podmínka postačující.
Může se jednat o inflexní bod nebo lokální extrém (minimum nebo maximum). Zkuste ověřit, že nalezený bod je skutečně minimum funkce Ep.
Celkové řešení
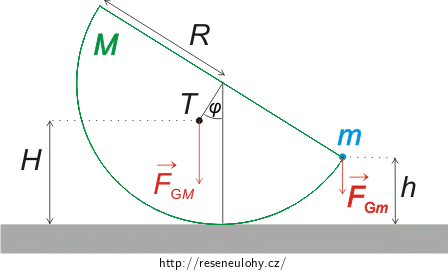
Do obrázku níže jsme zakreslili tíhovou sílu \(\vec{F_{GM}}\), která působí na samotnou polokouli v jejím těžišti, a sílu \(\vec{F_{Gm}}\) působící na samotné závaží.
Chceme najít stabilní rovnovážnou polohu polokoule se závažím, tedy příslušný úhel φ (viz obrázek).
Z mechaniky je známo, že těleso má tendenci zaujmout takovou polohu, při které je jeho potenciální energie tíhová minimální.
Poznámka: Potenciální energie tíhová nabýva minima v rovnovážné poloze stálé (stabilní), nikoli vratké.
Vzorec pro potenciální energii tíhovou je nám známý již ze střední školy
\[E_{\mathrm{p}} = mgh ,\]kde jsme za nulovou hladinu potenciální energie zvolili podložku, na které se nachází polokoule se závažím.
Pro potenciální energii tíhovou polokoule se závažím platí (viz obrázek nahoře)
\[ E_{\mathrm{p}} = M g H + m g h , \] kde H je vzdálenost těžiště T polokoule od podložky a h je vzdálenost závaží od podložky.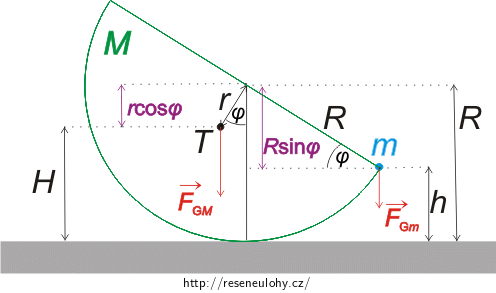
Po dosazení za H, h pomocí obrázku výše dostáváme
\[ E_{\mathrm{p}} = Mg(R - r\cos\varphi) + mg(R - R\sin\varphi) \] \[ E_{\mathrm{p}} = Mg(R - r\cos\varphi) + mgR(1 - \sin\varphi) . \]Máme najít extrém funkce. Nutnou podmínkou pro extrém je nulová první derivace (existuje-li).
Zderivujeme proto potenciální energii tíhovou podle úhlu φ, čímž dostáváme
\[ \frac{\mathrm{d}E_{\mathrm{p}}}{\mathrm{d}\varphi} = \frac{\mathrm{d}}{\mathrm{d}\varphi}\bigg[Mg(R - r\cos\varphi) + mgR(1 - sin\varphi)\bigg] \] \[ \frac{\mathrm{d}E_{\mathrm{p}}}{\mathrm{d}\varphi} = - Mgr(-\sin\varphi) - mgR\cos\varphi \] \[ \frac{\mathrm{d}E_{\mathrm{p}}}{\mathrm{d}\varphi} = Mgr\sin\varphi - mgR\cos\varphi . \]Položme nyní derivaci rovnu nule
\[ \frac{\mathrm{d}E_{\mathrm{p}}}{\mathrm{d}\varphi} = 0 \] \[ Mgr\sin\varphi - mgR\cos\varphi = 0 \] \[ Mgr\sin\varphi = mgR\cos\varphi . \]Po vydělení obou stran rovnice velikostí tíhového zrychlení g dostáváme
\[ Mr\sin\varphi = mR\cos\varphi, \]provedeme několik jednoduchých úprav
\[ \frac{\sin \varphi}{\cos{\varphi}} = \frac{mR}{Mr} \] \[ \mathrm{tg}\varphi = \frac{mR}{Mr}, \]aplikací inverzní funkce dostáváme
\[ \varphi= \mathrm{arctg}\left(\frac{mR}{Mr} \right). \]Nalezli jsme tak podmínku pro úhel φ a máme tak kandidáta na extrém funkce Ep .
Podmínka \[\frac{\mathrm{d}E_{\mathrm{p}}}{\mathrm{d}\varphi} = 0\] je nutná podmínka extrému, nikoli podmínka postačující.
Může se jednat o inflexní bod nebo lokální extrém (minimum nebo maximum). Zkusíme proto ověřit, že nalezený bod je skutečně minimum funkce Ep.
Spočteme druhou derivaci funkce Ep a podíváme se na její znaménko pro nalezené φ
\[ \frac{\mathrm{d}^2E_{\mathrm{p}}}{\mathrm{d}\varphi^2} = \frac{\mathrm{d}}{\mathrm{d}\varphi}(Mgr\sin\varphi - mgR\cos\varphi) \] \[ \frac{\mathrm{d}^2E_{\mathrm{p}}}{\mathrm{d}\varphi^2} = Mgr\cos\varphi + mgR\sin\varphi. \]Po dosazení za úhel φ dostaneme
\[ \frac{\mathrm{d}^2E_{\mathrm{p}}}{\mathrm{d}\varphi^2} = Mgr\cos\left(\mathrm{arctg}\left(\frac{mR}{Mr}\right) \right) + mgR\sin\left(\mathrm{arctg}\left(\frac{mR}{Mr} \right)\right). \]Funkce arkus tangens nabývá v tomto případě jenom kladných hodnot, protože výraz \[\frac{mR}{Mr}\] v jeho argumentu je kladný (žádná z konstant M, R, r, m nemůže být záporná). Z toho vyplývá, že v argumentu sinu a kosinu je také číslo kladné a zároveň menší než π/2 (arkus tangens nabývá hodnot menších než π/2). Funkce sinus a kosinus nabývají na intervalu (0, π/2) jenom kladných hodnot.
Součet dvou kladných čísel je kladné číslo, a tedy platí
\[ \frac{\mathrm{d}^2E_{\mathrm{p}}}{\mathrm{d}\varphi^2} \left(\varphi = \mathrm{arctg}\left(\frac{mR}{Mr}\right)\right) > 0. \]Funkce Ep proto nabývá lokálního minima pro \[\varphi = \mathrm{arctg}\left(\frac{mR}{Mr}\right).\]
Odpověď
Homogenní polokoule, na jejímž okraji je napevno umístěné navíc závaží, zaujme stabilní rovnovážnou polohu pro úhel \[\varphi = \mathrm{arctg}\left(\frac{mR}{Mr}\right).\]
Poznámka: Pro m = 0, tj. pro polokouli bez závaží dostáváme φ = 0, což je správně, protože díky homogenitě a symetrii polokoule není důvod, aby polokoule zaujala stabilní rovnovážnou polohu pro nenulový úhel φ.

