Začneme obecným vztahem pro polohu těžiště. Využijeme pouze y-ovou složku (Γ u integrálu znamená, že budeme integrovat přes celou křivku, tedy celý oblouk cykloidy).
\[y_T= \frac {\int_\Gamma y\ \mathrm d m}{\int_\Gamma \mathrm d m}\]
Protože se jedná o homogenní objekt, je možné integrál ve jmenovateli výrazně zjednodušit - integrování všech malých kousků hmotnosti přes celý oblouk cykloidy nám jistě dá celkovou hmotnost jednoho oblouku
\[y_T= \frac {\int_\Gamma y\ \mathrm d m}{m}\]
V čitateli by se nám přes kousky hmotnosti integrovalo už špatně. Nahradíme tedy integrování přes hmotnost integrováním přes objem V. Využijeme k tomu jednoduše vzorec z definice objemové hustoty hmotnosti
\[m=\rho V\]
\[\mathrm d m=\rho\ \mathrm d V\]
Objem se nám dále zjednoduší velmi rychle, protože cykloida je pouze jednorozměrný útvar – nemá jiných rozměrů, než své délky s.
\[\mathrm d V\Rightarrow \mathrm d s\]
Vztah pro souřadnici těžiště má nyní tvar
\[y_T= \frac {\int_\Gamma y \rho\ \mathrm d s}{m}.\]
ds představuje malý kousek křivky, ten ale potřebujeme v parametrickém vyjádření, protože cykloidu umíme psát v parametrickém tvaru. Musíme tedy nahradit ds vzorcem pro délku elementu obecné křivky
\[ \mathrm{d} s= \sqrt{\left( \frac{\mathrm{d} x}{\mathrm{d} t} \right)^2+ \left( \frac{\mathrm{d} y}{\mathrm{d} t} \right)^2} \mathrm{d} t\]
\[y_T= \frac {1}{m} \int_\Gamma \rho y \ \sqrt{\left( \frac{\mathrm{d} x}{\mathrm{d} t} \right)^2+ \left( \frac{\mathrm{d} y}{\mathrm{d} t} \right)^2} \mathrm{d} t.\tag{1}\]
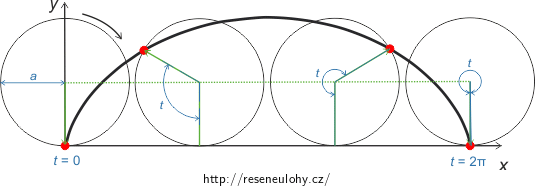
Dále potřebujeme zjistit, jak se mění souřadnice x a y s měnícím se parametrem. To nám umožní parametrické rovnice cykloidy
\[x=a (t-\sin t)\]
\[y=a (1-\cos t),\]
Pro naše účely si musíme připravit derivace parametrických rovnic cykloidy
\[\frac{\mathrm{d}x}{\mathrm{d}t}=a(1-\cos t)\]
\[\frac{\mathrm{d}y}{\mathrm{d}t}=a\sin t.\]
Po dosazení do rovnice (1)
\[y_T=\frac{1}{m} \int_\Gamma \rho\ a(1-\cos t) \sqrt{a^2(1-\cos t)^2 + a^2 sin^2 t}\ \mathrm d t\]
Nyní je zapotřebí upravit rovnici do takové podoby, kterou dokážeme integrovat. Jako první lze snadno určit integrační meze. Víme, že integrujeme přes parametr t a to přes jeden celý oblouk cykloidy. Pro jeden oblouk nabývá parametr t hodnot od 0 do 2π – to budou tedy naše integrační meze. Dále je výhodné vytknout co nejvíce konstant před integrál. V našem případě je to ρ a a2.
\[y_T=\frac{a^2 \rho}{m} \int_0^{2\pi} \ (1-\cos t) \sqrt{(1-\cos t)^2 + sin^2 t}\ \mathrm d t \]
V dalších krocích se postupně snažíme upravit integrál tak, abychom došli k tvaru, který buď dokážeme přímo integrovat, nebo tvaru, na který bude možné použít substituci. Často se k tomu využívají goniometrické vzorce, které je nutné dobře znát.
\[y_T=\frac{a^2 \rho}{m} \int_0^{2\pi} \ (1-\cos t) \sqrt{1-2\cos t + \cos^2 t + \sin^2 t}\ \mathrm d t\]
Zde se uplatní tzv. goniometrická jednička.
\[y_T=\frac{a^2 \rho}{m} \int_0^{2\pi} \ (1-\cos t) \sqrt{2-2\cos t }\ \mathrm d t\]
\[y_T=\frac{a^2 \rho}{m} \int_0^{2\pi} \ (1-\cos t) \sqrt 2 \sqrt{1-\cos t }\ \mathrm d t\]
\[y_T=\frac{a^2 \rho}{m} \int_0^{2\pi} \ \sqrt 2 (\sqrt{1-\cos t })^3\ \mathrm d t\]
Výraz pod třetí mocninou má velmi blízko dalšímu goniometrickému vzorci, k němuž se tedy pokusíme přiblížit
\[|\sin {\frac {t}{2}}|=\sqrt{\frac{1-\cos t}{2}}.\]
\[y_T=\frac{a^2 \rho}{m} \int_0^{2\pi} \ \sqrt 2 (\sqrt{1-\cos t })^3\ \mathrm d t \cdot \frac {(\sqrt2)^3}{(\sqrt2)^3}\]
\[y_T=\frac{a^2 \rho}{m} \int_0^{2\pi} \ 4 \left(\sqrt{\frac {1-\cos t}{2} }\right)^3\ \mathrm d t\]
\[y_T=\frac{4a^2 \rho}{m} \int_0^{2\pi} \ \left|\sin\frac{t}{2}\right|^3\ \mathrm d t\]
Absolutní hodnota by nám mohla zdánlivě vadit, ale můžeme ji jednoduše zanedbat. Sinus bude v našem integrálu nabývat pouze hodnot od 0 do 1; (integrační meze jsou od 0 do 2π a v sinu jsou děleny 2) a na tomto intervalu je sinus pouze kladný nebo nula. Poté bude možné použít substituci. Nesmíme zapomenout přepočítat integrační meze!
\[y_T=\frac{4a^2 \rho}{m} \int_0^{2\pi} \ \left(\sin\frac{t}{2}\right)^3\ \mathrm d t
\begin{vmatrix}u=\frac{t}{2} \\\mathrm d u =\frac{1}{2} \mathrm d t \\2 \mathrm d u = \mathrm d t \end{vmatrix}\]
\[y_T=\frac{4a^2 \rho}{m} \int_0^{\pi} 2\sin^3 u\ \mathrm d u\]
Ani tento integrál ještě neumíme přímo integrovat, je tedy zapotřebí dalších úprav a další substituce. Tento postup není nijak výjimečný, ale zprvu se může zdát obtížný.
\[y_T=\frac{8^2 a \rho}{m} \int_0^{\pi} \sin^2 u\ \sin u\ \mathrm d u\]
\[y_T=\frac{8a^2 \rho}{m} \int_0^{\pi} (1-\cos^2 u)\ \sin u\ \mathrm d u
\begin{vmatrix}w=\cos u \\\mathrm d w =- \sin u\ \mathrm d u \\-\frac{1}{\sin u} \mathrm d w= \mathrm d u \end{vmatrix}
\]
\[y_T=\frac{8a^2 \rho}{m} \int_1^{-1} (1-w^2)\ \sin u\ \frac {1}{-\sin u} \mathrm d w \]
Takto napsané integrační meze jsou naprosto v pořádku, i když není obvyklé, že dolní mez vychází větší, než horní.
\[y_T=\frac{8a^2 \rho}{m} \int_1^{-1} -(1-w^2)\ \mathrm d w \]
\[y_T=\frac{8a^2 \rho}{m} \left[\frac{1}{3}w^3-w\right]_1^{-1}\]
\[y_T=\frac{8a^2 \rho}{m} \frac{4}{3}\]
Protože hustotu nemáme zadanou, je zapotřebí ji nahradit. Můžeme využít toho, že známe hmotnost a objem cykloidy a uvědomit si opět fakt, že cykloida nemá jiné rozměry, než svou délku s.
\[\rho=\frac{m}{s}\]
\[y_T=\frac{8a^2 m}{sm} \frac{4}{3}\]
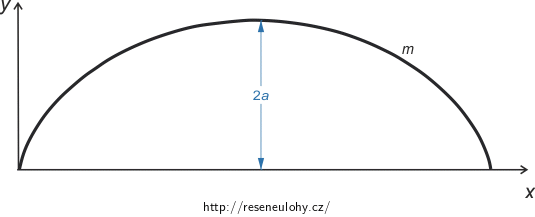
Délka jednoho oblouku cykloidy s je rovna osminásobku poloměru kružnice, která ji svým valením vytvořila (nebo čtyřnásobku své výšky) (viz Délka oblouku cykloidy). Pro y-ovou souřadnici těžiště jednoho oblouku homogenní cykloidy tedy dostáváme:
\[y_T=\frac{4}{3}a\]
Těžiště oblouku cykloidy tedy leží ve 2/3 její výšky.