Potenciál výsledného gravitačního pole mezi Zemí a Měsícem

Úloha číslo: 520

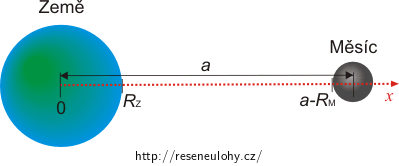
Najděte vztah pro gravitační potenciál V(x) na spojnici mezi Zemí a Měsícem jako funkci proměnné x, kde x je vzdálenost měřená od středu Země a a je vzdálenost středů obou vesmírných těles, a to pro x z intervalu (R_Z; a − R_M).

Zjistěte, zda potenciál nabývá někde na spojnici těles extrémních hodnot, a vysvětlete jejich fyzikální význam.

Vyjděte z výsledků úlohy Intenzita gravitačního pole mezi Zemí a Měsícem. Navrhněte možná řešení úlohy.

Teorie – potenciál gravitačního pole
Potenciál je skalární veličina určující potenciální energii tělesa jednotkové hmotnosti v závislosti na jeho umístění v prostoru.

Silové pole označujeme jako konzervativní právě tehdy, když práce vykonaná při pohybu mezi dvěma body v tomto poli nezávisí na tvaru trajektorie mezi těmito dvěma body. Gravitační pole Země a Měsíce jsou příkladem konzervativního pole.

Potenciál je možno zavést pouze pro konzervativní silová pole.

Potenciál gravitačního pole vně tělesa generujícího gravitační pole můžeme zapsat vztahem:
\[V(r) = -\kappa \frac{M}{r}\,,\]
kde κ je gravitační konstanta, M je hmotnost tělesa generujícího gravitační pole a r je vzdálenost zkoumaného bodu od středu tohoto tělesa. Nulovou hladinu potenciálu volíme v nekonečnu.

Pro vztah mezi potenciálem gravitačního pole V a intenzitou gravitačního pole \(\vec{K}\) platí:
\[\vec{K} = -\mathrm{grad}\,V.\]
Pokud je tedy těleso v rovnovážné poloze (intenzita je nulová), pak potenciál nabývá extrému.
Nápověda 1
Popište vzhledem k udané souřadnici x intenzitu gravitačního pole na spojnici mezi Zemí a Měsícem.
Řešení nápovědy 1
Vztah pro velikost výsledné intenzity gravitačního pole na spojnici mezi Zemí a Měsícem v závislosti na vzdálenosti x od středu Země je odvozen v úloze Intenzita gravitačního pole mezi Zemí a Měsícem:
\[K(x) = -\kappa \frac{M}{x^2} + \kappa \frac{m}{(a-x)^2},\] kde M je hmotnost Země, m je hmotnost Měsíce a x je z intervalu (R_Z; a − R_M).
Nápověda 2
Uvědomte si vztah mezi intenzitou gravitačního pole a jeho potenciálem. Napište příslušnou rovnici a dosaďte do ní.
Řešení nápovědy 2
\[\vec{K} = -\mathrm{grad}\,V\]
Vzhledem k tomu, že úlohu řešíme pouze na spojnici mezi oběma tělesy, můžeme zjednodušit:
\[K(x) = -\frac{dV(x)}{dx}\,.\]
Dosadíme už známé:
\[-\kappa \frac{M}{x^2} + \kappa \frac{m}{(a-x)^2} = -\frac{dV(x)}{dx}\,.\]
Obecně:
\[V(x_1)-V(x_2) = \int_{x_1}^{x_2}K(x) dx\mathrm{,\,\,\, pro}\,\ x_1 < x_2\,.\]
V našem případě:
\[V(x)-V(+\infty) = \int_{x}^{\infty}K(x) dx,\,\,\, \mathrm{kde}\,\ V(+\infty) = 0\,,\] \[V(x) = \int_{x}^{\infty} (-\kappa \frac{M}{x^2} + \kappa \frac{m}{(a-x)^2}) dx = 0-(\kappa \frac{M}{x} + \kappa \frac{m}{a-x})\,,\] \[V(x) = -\kappa \frac{M}{x} - \kappa \frac{m}{a-x}\,.\]
Nápověda 3
Jak najdeme místo, kde potenciál nabývá extrému? Můžeme buď zkoumat vztah, který jsme pro potenciál mezi Zemí a Měsícem odvodili, nebo můžeme využít vztahu mezi intenzitou a potenciálem gravitačního pole a výsledků úlohy Intenzita gravitačního pole mezi Zemí a Měsícem.
Řešení nápovědy 3
Extrém funkce V(x) zjistíme, položíme-li její derivaci podle x rovnu nule.

Z řešení Nápovědy 2 víme, že:
\[\frac{dV(x)}{dx} = \kappa \frac{M}{x^2} - \kappa \frac{m}{(a-x)^2}\,.\]
Pro souřadnici x₀, kde funkce nabývá extrému, platí:
\[\kappa \frac{M}{x_0^2} - \kappa \frac{m}{(a-x_0)^2} = 0\,,\] \[\frac{M}{x_0^2} - \frac{m}{(a-x_0)^2} = 0\,,\] \[M (a-x_0)^2 = m x_0^2\,.\]
Odmocníme:
\[\sqrt{M}(a-x_0) = \sqrt{m}x_0\,.\]
Odtud:
\[x_0 = a \frac{\sqrt{M}}{\sqrt{M}+\sqrt{m}}\,.\]
Na spojnici mezi Zemí a Měsícem se bude nalézat jediný extrém, a to v bodě o výše uvedené souřadnici x₀.

Dalším vyšetřováním zjistíme, že se jedná o maximum funkce.

Ke stejnému závěru nás dovede i úvaha na základě vztahu intenzity a potenciálu gravitačního pole s využitím výsledků úlohy Intenzita gravitačního pole mezi Zemí a Měsícem. Platí:
\[K(x) = -\frac{dV(x)}{dx}\,.\]
Má-li tedy V(x) v nějakém bodě x₀ extrém, pak nutnou podmínkou je, aby K(x₀) bylo rovno nule. Kde se tento bod nachází, už z úlohy Intenzita gravitačního pole mezi Zemí a Měsícem víme. Zbývá vyšetřit povahu extrému.

Poznámka: Ověření, že jde o maximum funkce:
\[\frac{d^2V(x)}{dx^2} = \frac{d}{dx} (\kappa \frac{M}{x^2} - \kappa \frac{m}{(a-x)^2}) = -2\kappa \frac{M}{x^3} - 2\kappa \frac{m}{(a-x)^3}\] \[\frac{d^2V(x)}{dx^2}= -2\kappa (\frac{M}{x^3}+\frac{m}{(a-x)^3})<0 \]
Nápověda 4
Bylo řečeno, že pokud je intenzita gravitačních sil působících na těleso nulová, pak nabývá potenciál extrému a těleso se nachází v rovnovážné poloze.

Jaký vztah k sobě mají skutečnosti, že se těleso nachází v rovnovážné poloze stabilní nebo labilní a potenciál nabývá maxima nebo minima?

Uvědomte si, co se stane, pokud se těleso z rovnovážné polohy vychýlí.
Řešení nápovědy 4
Těleso je přitahováno Zemí i Měsícem. Bude-li tedy vychýleno z rovnovážné polohy, jedna z přitažlivých sil „zvítězí“. Opustí-li těleso rovnovážnou polohu, už se do ní samovolně nevrátí, ale bude se od ní neustále vzdalovat. Je to tedy poloha labilní.

Při pádu k Zemi (resp. Měsíci) těleso svou potenciální energii ztrácí. V labilní rovnovážné poloze musí mít tedy potenciál maximum. Analogicky, pokud potenciál nabývá minima, pak je těleso v rovnovážné poloze stabilní.
Komentář – další způsoby řešení
V použitém řešení jsme se snažili těžit z výsledků úlohy Intenzita gravitačního pole mezi Zemí a Měsícem, tj. řešit problém alespoň částečným převedením na známý případ a ukázat vztahy mezi potenciálem a intenzitou gravitačního pole.

Stejně tak je ovšem úloha řešitelná v podstatě z definice potenciálu. Protože pro něj platí princip superpozice, je možné psát:
\[V = V_\mathrm{Zeme}+V_\mathrm{Mesice}\,,\]
což nás okamžitě zavede ke vztahu:
\[V(x) = -\kappa \frac{M}{x} - \kappa \frac{m}{a-x}\,.\]
Stejně tak by bylo možné pořadí úloh obrátit a z výsledků této úlohy určit průběh intenzity gravitačního pole mezi Zemí a Měsícem. Využili bychom vztah:
\[K(x) = -\frac{dV(x)}{dx}\,.\]
Celkové řešení
Vztah pro velikost výsledné intenzity gravitačního pole na spojnici mezi Zemí a Měsícem v závislosti na vzdálenosti x od středu Země je odvozen v úloze Intenzita gravitačního pole mezi Zemí a Měsícem:
\[K(x) = -\kappa \frac{M}{x^2} + \kappa \frac{m}{(a-x)^2}\,,\] kde M je hmotnost Země, m je hmotnost Měsíce a x je z intervalu (R_Z; a − R_M).
Potenciál gravitačního pole vně tělesa generujícího gravitační pole můžeme zapsat vztahem:
\[V(r) = -\kappa \frac{M}{r}\,,\]
kde κ je gravitační konstanta, M je hmotnost tělesa generujícího gravitační pole a r je vzdálenost zkoumaného bodu od středu tohoto tělesa. Nulovou hladinu potenciálu volíme v nekonečnu.

Pro vztah mezi potenciálem gravitačního pole V a intenzitou gravitačního pole \(\vec{K}\) platí:
\[\vec{K} = -\mathrm{grad}\,V\,.\]
Vzhledem k tomu, že úlohu řešíme pouze na spojnici mezi oběma tělesy, můžeme zjednodušit:
\[K(x) = -\frac{dV(x)}{dx}\,.\]
Dosadíme už známé:
\[-\kappa \frac{M}{x^2} + \kappa \frac{m}{(a-x)^2} = -\frac{dV(x)}{dx}\,.\]
Obecně:
\[V(x_1)-V(x_2) = \int_{x_1}^{x_2}K(x) dx\mathrm{,\,\,\, pro\,\ }x_1 < x_2\,.\]
V našem případě:
\[V(x)-V(+\infty) = \int_{x}^{\infty}K(x) dx\mathrm{,\,\ kde\ \,}V(+\infty) = 0,\] \[V(x) = \int_{x}^{\infty} (-\kappa \frac{M}{x^2} + \kappa \frac{m}{(a-x)^2}) dx = 0-(\kappa \frac{M}{x} + \kappa \frac{m}{a-x})\,,\] \[V(x) = -\kappa \frac{M}{x} - \kappa \frac{m}{a-x}\,.\]
Extrém funkce V(x) zjistíme, položíme-li její derivaci podle x rovnu nule.

Z řešení Nápovědy 2 víme, že:
\[\frac{dV(x)}{dx} = \kappa \frac{M}{x^2} - \kappa \frac{m}{(a-x)^2}\,.\]
Pro souřadnici x₀, kde funkce nabývá extrému, platí:
\[\kappa \frac{M}{x_0^2} - \kappa \frac{m}{(a-x_0)^2} = 0\,,\] \[\frac{M}{x_0^2} - \frac{m}{(a-x_0)^2} = 0\,,\] \[M (a-x_0)^2 = m x_0^2\,.\]
Odmocníme:
\[\sqrt{M}(a-x_0) = \sqrt{m}x_0\,.\]
Odtud:
\[x_0 = a \frac{\sqrt{M}}{\sqrt{M}+\sqrt{m}}\,.\]
Na spojnici mezi Zemí a Měsícem se bude nalézat jediný extrém, a to v bodě o výše uvedené souřadnici x₀.

Dalším vyšetřováním zjistíme, že se jedná o maximum funkce.

Ke stejnému závěru nás dovede i úvaha na základě vztahu intenzity a potenciálu gravitačního pole s využitím výsledků úlohy Intenzita gravitačního pole mezi Zemí a Měsícem. Platí:
\[K(x) = -\frac{dV(x)}{dx}\,.\]
Má-li tedy V(x) v nějakém bodě x₀ extrém, pak nutnou podmínkou je, aby K(x₀) bylo rovno nule. Kde se tento bod nachází, už z úlohy Intenzita gravitačního pole mezi Zemí a Měsícem víme. Zbývá vyšetřit povahu extrému.

Těleso je přitahováno Zemí i Měsícem. Bude-li tedy vychýleno z rovnovážné polohy, jedna z přitažlivých sil „zvítězí“. Opustí-li těleso rovnovážnou polohu, už se do ní samovolně nevrátí, ale bude se od ní neustále vzdalovat. Je to tedy poloha labilní.

Při pádu k Zemi (resp. Měsíci) těleso svou potenciální energii ztrácí. V labilní rovnovážné poloze musí mít tedy potenciál maximum. Analogicky, pokud potenciál nabývá minima, pak je těleso v rovnovážné poloze stabilní.

Poznámka: Ověření, že jde o maximum funkce:
\[\frac{d^2V(x)}{dx^2} = \frac{d}{dx} (\kappa \frac{M}{x^2} - \kappa \frac{m}{(a-x)^2}) = -2\kappa \frac{M}{x^3} - 2\kappa \frac{m}{(a-x)^3}\] \[\frac{d^2V(x)}{dx^2}= -2\kappa (\frac{M}{x^3}+\frac{m}{(a-x)^3})<0 \]
Odpověď
Vztah udávající průběh potenciálu na spojnici mezi Zemí a Měsícem pro x z intervalu (R_Z; a − R_M):
\[V(x) = -\kappa \frac{M}{x} - \kappa \frac{m}{a-x}\,.\]
Potenciál bude mít extrém v bodě o souřadnici:
\[x_0 = a \frac{\sqrt{M}}{\sqrt{M}+\sqrt{m}}\,.\]
Těleso se tam nachází v rovnovážné poloze labilní.

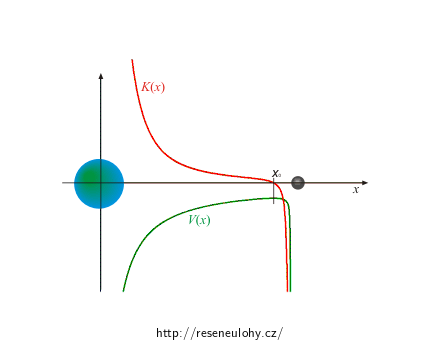
Poznámka: Graf je ilustrační, není zachováno měřítko u Země a Měsíce vzhledem k vzdálenosti jejich středů. Vzdálenost středů je asi 384 000 km, místo o nulové intenzitě (x₀) je ve vzdálenosti přibližně 346 000 km od středu Země.