Klouzání tyče
Úloha číslo: 1031
Konce tyče A, B (viz obrázek níže) kloužou po vzájemně kolmých polopřímkách OX a OY (konec tyče A klouže po polopřímce OX a konec B po polopřímce OY), přičemž konec tyče B se pohybuje rychlostí s konstantní velikostí v0.
a) Najděte obecnou rovnici trajektorie, po které se pohybuje bod tyče M znázorněný na obrázku.
b) Určete velikost rychlosti bodu M, víte-li, že v čase t = 0 tyč splývala s polopřímkou OY a bod A splýval s bodem O.
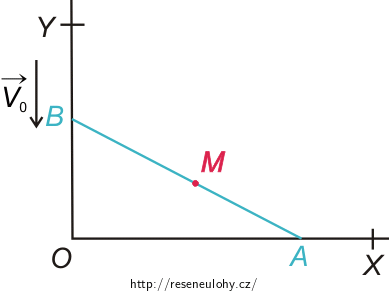
Poznámka 1: Bod M není uprostřed tyče, je to obecný bod tyče mimo její konce.
Poznámka 2: Tyč považujeme za tuhé těleso (tvar ani rozměry se nemění).
Nápověda 1 ( k úloze a) )
Nejdřív zaveďte kartézskou soustavu souřadnic. Parametrické vyjádření trajektorie, po které se pohybuje bod M, naleznete jednoduše.
Zamyslete se, jak přejdete od parametrického vyjádření k obecné rovnici trajektorie (křivky), po které se pohybuje bod M.
Nápověda 2 ( k úloze b) )
Úlohou je určit velikost rychlosti, jakou se pohybuje bod M.
Rozmyslete si, jak spočítáte složky vektoru rychlosti bodu M.
Velikost vektoru rychlosti z nich pak naleznete jednoduše, uvážíte-li, že jsou na sebe kolmé.
Nápověda 3 ( k úloze b) )
Ve vztahu pro velikost rychlosti se vyskytuje derivace úhlu α podle času, kterou zatím neznáme.
Zkuste se zamyslet, jak ji spočítáte. Využijte k tomu počáteční podmínku ze zadání úlohy.
Nakreslete si, jakou dráhu urazil konec tyče B za nějaký čas t.
Celkové řešení
ad a)
Zvolili jsme kartézskou soustavu souřadnic (viz obrázek níže). Bod M dělí tyč na dvě části, jejichž délku jsme označili a > 0, b > 0. Souřadnice bodu M jsme označili xM, yM.
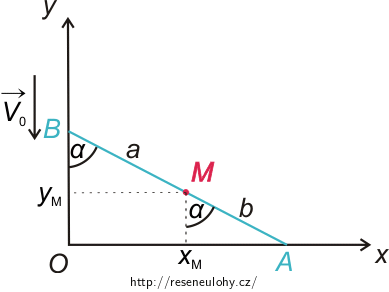
Parametrické vyjádření trajektorie, po které se pohybuje bod M, je následující (viz obrázek výše):
\[ x_{\mathrm{M}} = a\sin\alpha \] \[y_{\mathrm{M}} = b\cos\alpha .\]Vydělením a a b dostáváme
\[ \frac{x_{\mathrm{M}}}{a} = \sin\alpha \] \[ \frac{y_{\mathrm{M}}}{b} = \cos\alpha . \]Umocníme obě rovnice a sečteme je:
\[ \frac{x_{\mathrm{M}}^2}{a^2} = \sin^2\alpha \] \[ \frac{y_{\mathrm{M}}^2}{b^2} = \cos^2\alpha \] \[ \frac{x_{\mathrm{M}}^2}{a^2} + \frac{y_{\mathrm{M}}^2}{b^2} = \underbrace{\sin^2\alpha + \cos^2\alpha}_1 . \]Dostáváme tak obecnou rovnici elipsy
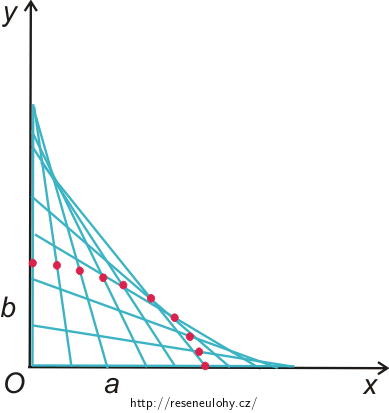
\[ \frac{x_{\mathrm{M}}^2}{a^2} + \frac{y_{\mathrm{M}}^2}{b^2} = 1 \hspace{45px}x_{\mathrm{M}} \ge 0 ,\hspace{5px} y_{\mathrm{M}} \ge 0. \]Jedná se o část elipsy (1. kvadrant) s poloosami a a b a se středem [0, 0] (viz obrázek níže).
ad b)
Složky vektoru rychlosti získáme derivací souřadnic polohy bodu M podle času.
Poznámka: Úhel α je funkcí času, takže derivujeme složenou funkci.
\[ v_{\mathrm{x}} = \frac{\mathrm{d}x_{\mathrm{M}}} {\mathrm{d}t} = \frac{\mathrm{d}}{\mathrm{d}t}(a\sin\alpha) = a\cos\alpha \frac{\mathrm{d}\alpha}{\mathrm{d}t} \] \[ v_{\mathrm{y}} = \frac{\mathrm{d}y_{\mathrm{M}}} {\mathrm{d}t} = \frac{\mathrm{d}}{\mathrm{d}t}(b\cos\alpha) = -b\sin\alpha \frac{\mathrm{d}\alpha}{\mathrm{d}t} . \]Pro velikost rychlosti platí (vycházíme z Pythagorovy věty)
\[ v = \sqrt{v_{\mathrm{x}}^2 + v_{\mathrm{y}}^2 } \] \[ v = \sqrt{a^2\cos^2\alpha \left(\frac{\mathrm{d}\alpha}{\mathrm{d}t}\right)^2 + b^2\sin^2\alpha \left(\frac{\mathrm{d}\alpha}{dt}\right)^2} \] \[ v = \sqrt{\left(\frac{\mathrm{d}\alpha}{\mathrm{d}t}\right)^2\left(a^2\cos^2\alpha + b^2\sin^2\alpha \right)} \] \[ v = \left|\frac{\mathrm{d}\alpha}{\mathrm{d}t}\right | \sqrt{a^2\cos^2\alpha + b^2\sin^2\alpha }. \]Víme, že derivace úhlu α představuje „jeho změnu v čase“. V úloze se předpokládá jenom klouzání tyče „směrem dolů“, přičemž se úhel α zvětšuje. To znamená, že derivace je nezáporná, a proto lze absolutní hodnotu vynechat.
Ve vztahu pro velikost rychlosti se vyskytuje derivace úhlu α podle času, kterou zatím neznáme.
Víme, že v čase t = 0 tyč splývala s osou y a bod A splýval s bodem O.
Do obrázku, který je možné vidět níže, jsme zakreslili dráhu, kterou urazí konec tyče B za čas t. A(1), B(1) označují konce tyče v první poloze (v čase t = 0), analogicky A(2), B(2) označují konce tyče po uplynutí času t.
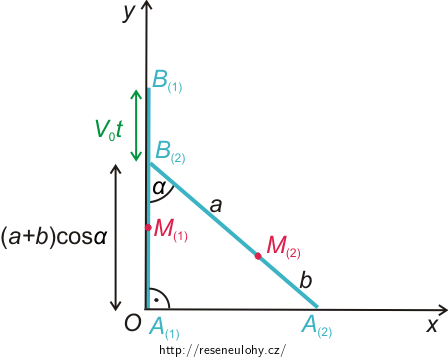
Za čas t urazil konec tyče B dráhu
\[ v_0t = (a + b) - (a + b)\cos\alpha, \]zderivujeme obě strany rovnice podle času t
\[ v_0 = - (a + b)(-\sin\alpha)\frac{\mathrm{d}\alpha}{\mathrm{d}t} \] \[ v_0 = (a + b)\sin\alpha\frac{\mathrm{d}\alpha}{\mathrm{d}t} \]a pro časovou derivaci úhlu α dostáváme
\[ \frac{\mathrm{d}\alpha}{\mathrm{d}t} = \frac{v_0}{(a + b)\sin\alpha}. \]Výše jsme vyjádřili velikost rychlosti
\[ v = \frac{\mathrm{d}\alpha}{\mathrm{d}t}\sqrt{a^2\cos^2\alpha + b^2\sin^2\alpha }. \]Nyní dosadíme za výraz \[\frac{\mathrm{d}\alpha}{\mathrm{d}t}=\frac{v_0}{(a + b)\sin\alpha} \]
\[ v = \frac{v_0}{(a + b)\sin\alpha} \sqrt{a^2\cos^2\alpha + b^2\sin^2\alpha } \] \[ v = \frac{v_0}{a + b}\sqrt{a^2\hspace{1px}\frac{\cos^2\alpha}{\sin^2\alpha} + b^2\hspace{1px} \frac{\sin^2\alpha}{\sin^2\alpha}}. \]Dostáváme tak hledanou velikost rychlosti
\[ v = \frac{v_0}{a + b}\sqrt{a^2\hspace{1px} \mathrm{cotg}^2\alpha \hspace{1px}+ \hspace{1px}b^2}. \]Poznámka: V zadání jsme předpokládali konstantní velikost rychlosti v0. Vidíme, že se ve vztahu pro velikost rychlosti nachází funkce kotangens, která pro \(\alpha \rightarrow 0^{+} \) roste nade všechny meze, což by znamenalo, že také velikost rychlosti roste nade všechny meze. To je nereálné, takže odvozený vztah nelze použít pro popis pohybu tyče pro t blízké 0 s.
Odpověď
a) Obecná rovnice trajektorie, po které se pohybuje bod M, je následující \[ \hspace{20px} \frac{x_{\mathrm{M}}^2}{a^2} + \frac{y_{\mathrm{M}}^2}{b^2} = 1 \hspace{45px}x_{\mathrm{M}} \ge 0 ,\hspace{5px} y_{\mathrm{M}} \ge 0\ . \]
Jedná se o část elipsy (1. kvadrant) s poloosami a a b a se středem [0, 0].
b) Pro velikost rychlosti bodu M platí
\[ v = \frac{v_0}{a + b}\sqrt{a^2\hspace{1px} \mathrm{cotg}^2\alpha \hspace{1px}+ \hspace{1px}b^2}. \]

