Sbírka řešených úloh

Měření vodivosti mořské vody

Úloha číslo: 306

• I. Nápovědy

• Nápověda 1

  Prostor mezi vodiči si rozdělte na tenké kulové sféry o poloměru r, kde a < r < b, a „tloušťce” dr.

  

  Celý vodič je nyní sériovým zapojením těchto slupek a celkový odpor vodiče bude tedy roven součtu odporů jednotlivých sfér.

• Nápověda 2

  Uvědomte si, jak vypočítáme elektrický odpor jedné kulové sféry v závislosti na rozměrech a vodivosti materiálu.

• Řešení nápovědy 2

  Elektrický odpor homogenního vodiče R je nepřímo úměrný vodivosti materiálu σ:

  \[ R\,=\,\frac{1}{\sigma}\,\frac{l}{S}\,, \]

  kde l je délka vodiče a S je obsah jeho průřezu.

  Celý vodič jsme rozdělili na tenké kulové sféry o poloměru r. „Plocha“ (povrch) každé sféry se rovná 4πr² a její „délku“ označíme dr. Každá sféra o poloměru r má tedy odpor:

  \[ \mathrm{d}R\,=\,\frac{1}{\sigma}\,\frac{\mathrm{d}r}{4\pi r^2}\,. \]

• I. Rozbor

  Prostor mezi vodiči rozdělíme na tenké kulové plochy o poloměru r, kde a < r < b.

  

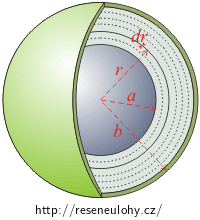
  Celý vodič nyní můžeme brát jako sériové zapojení těchto sfér. Celkový odpor vodiče tedy získáme součtem (integrací) odporů jednotlivých sfér.

  Elektrický odpor kulové sféry je přímo úměrný její „délce“ a nepřímo úměrný ploše slupky a vodivosti materiálu.

  Proud procházející mezi elektrodami se rovná podílu napětí a elektrického odporu mezi elektrodami.

• I. Řešení

  Prostor mezi elektrodami si rozdělíme na tenké slupky (kulové sféry) o poloměru r (a < r < b) a „tloušťce“ dr.

  

  Elektrický odpor slupky vypočítáme ze vztahu:

  \[ R\,=\,\frac{1}{\sigma}\,\frac{l}{S}\,, \]

  kde σ je vodivost materiálu, l délka vodiče a S plocha jeho průřezu.

  V tomto případě „plocha“ slupky odpovídá povrchu kulové sféry, tedy 4πr². „Délku“ slupky označíme dr. Odpor dR kulové slupky o poloměru r pak vyjádříme vztahem:

  \[ \mathrm{d}R\,=\,\frac{1}{\sigma}\,\frac{\mathrm{d}r}{4\pi r^2}\,. \]

  Protože jsou slupky zapojeny sériově, bude celkový odpor mezi kulovými elektrodami roven součtu (integraci) všech slupek dR od poloměru a do poloměru b:

  \[ R\,=\,\int_\mathrm{a}^\mathrm{b}\,\frac{1}{\sigma}\,\frac{\mathrm{d}r}{4\pi r^2}\,=\, \frac{1}{4\pi \sigma}\int_\mathrm{a}^\mathrm{b}\frac{\mathrm{d}r}{r^2}\,=\,\frac{1}{4\pi \sigma}\,\left[-\frac{1}{r}\right]_\mathrm{a}^\mathrm{b} \,. \]

  Celkový elektrický odpor mezi kulovými elektrodami tedy vypočítáme:

  \[ R\,=\,\frac{1}{4\pi\sigma}\,\left(\frac{1}{a}\,-\,\frac{1}{b}\right) \] \[ R\,=\,\frac{1}{4\pi\sigma}\,\frac{b-a}{ab} \] \[ R\,=\,\frac{b-a}{4\pi\sigma ab}\,. \]

  Proud I procházející mezi elektrodami se rovná podílu napětí U a elektrického odporu R mezi elektrodami:

  \[ I\,=\,\frac{U}{R}\,=\,\frac{4\pi\sigma ab}{b-a}\,U\,. \]

• II. Nápovědy

• Nápověda 1

  Vyhledejte si vztah pro Ohmův zákon v diferenciálním tvaru.

• Řešení nápovědy 1

  Vztah pro Ohmův zákon v diferenciálním tvaru zní:

  \[ \vec{j\,}=\,\sigma \vec{E}\,, \]

  kde \(\vec{j\,}\) značí hustotu elektrického proudu, σ je měrná elektrická vodivost a \(\vec{E}\) intenzita elektrického pole.

• Nápověda 2

  Pomocí intenzity elektrického pole určete velikost napětí mezi kulovými elektrodami.

  Celkový odpor vodiče pak bude roven podílu napětí mezi elektrodami a celkového proudu, který mezi elektrodami prochází.

• Řešení nápovědy 2

  Díky elektrickému poli vodiče se mezi konci vodiče vytváří napětí U. Toto napětí se rovná rozdílu elektrických potenciálů zmiňovaných konců vodiče.

  Mezi elektrickou intenzitou \(\vec{E}\) a potenciálem \(\varphi\) v bodě P platí:

  \[ \varphi =-\int_0^\mathrm{P} \vec{E}\cdot\mathrm{d}\vec{r\,}, \]

  kde integrujeme z místa, kde jsme zvolili nulový potenciál, do místa P (integrál nezávisí na zvolené integrační cestě).

  Napětí mezi soustřednými kulovými elektrodami o poloměrech a, b (a < b) je tedy rovno rozdílu potenciálů v těchto bodech:

  \[ U\,=\,\varphi_{(a)}\,-\,\varphi_{(b)}\,=\,-\int_0^\mathrm{a}\vec{E}\cdot\mathrm{d}\vec{r\,}\,+\,\int_0^\mathrm{b}\vec{E}\cdot\mathrm{d}\vec{r\,} \] \[ U\,=\,\int_0^\mathrm{b}\vec{E}\cdot\mathrm{d}\vec{r\,}\,-\,\int_0^\mathrm{a}\vec{E}\cdot\mathrm{d}\vec{r\,}\,=\, \int_\mathrm{a}^\mathrm{b} \vec{E}\cdot\mathrm{d}\vec{r\,}. \]

• II. Rozbor

  Prostor mezi kulovými vodiči rozdělíme na tenké kulové sféry o poloměru r, kde a < r < b.

  

  Z kulové symetrie situace vyplývá, že ve všech místech takto vytvořené sféry je stejná hustota proudu. Tu můžeme vyjádřit pomocí celkového proudu a plochy sféry. Celkový proud mezi elektrodami je stálý, nezávislý na poloměru r.

  Ohmův zákon v diferenciálním tvaru pro homogenní vodiče říká, že hustota proudu procházejícího vodičem se rovná součinu měrné elektrické vodivosti a intenzity elektrického pole vodiče. Z tohoto zákona si vyjádříme intenzitu elektrického pole.

  Integrací intenzity elektrického pole získáme napětí mezi elektrodami. Celkový odpor materiálu pak určíme jako podíl napětí mezi elektrodami a proudu, který mezi elektrodami prochází.

• II. Řešení

  Prostor mezi kulovými elektrodami si rozdělíme na tenké kulové slupky o poloměru r, přičemž a < r < b. Z kulové symetrie situace vyplývá, že ve všech místech takové slupky je stejná hustota proudu j. Pro celkový proud procházející slupkou tedy platí:

  \[ I=S\,j\left(r\right)=4\pi r^2\,j\left(r\right)\,. \]

  Celkový proud mezi elektrodami je stálý a není tedy závislý na poloměru r.

  Z diferenciálního tvaru Ohmova zákona pro homogenní vodič

  \[ \vec{j\,}=\,\sigma\vec{E}, \]

  kde \(\sigma\) je měrná elektrická vodivost a \(\vec{E}\) intenzita elektrického pole, určíme velikost intenzity elektrického pole v kulové slupce o poloměru r:

  \[ E\left(r\right)\,=\,\frac{j\left(r\right)}{\sigma}\,. \]

  Stejně jako hustota proudu j(r), tak i velikost intenzity elektrického pole E(r) závisí pouze na poloměru slupky r. Hustotu proudu j(r) v kulovém vodiči o poloměru r získáme ze vztahu pro celkový proud a dosadíme do vzorce pro výpočet intenzity elektrického pole:

  \[ E\left(r\right)\,=\,\frac{I}{4\pi r^2\sigma}\,. \]

  Napětí U mezi elektrodami získáme integrací intenzity elektrického pole:

  \[ U\,=\,\int_\mathrm{a}^\mathrm{b} \vec{E}\left(r\right)\cdot \mathrm{d}\vec{r\,}. \]

  Díky kulové symetrii situace bude intenzita elektrického pole mířit v každém bodě vodiče radiálním směrem. Vektory \(\vec{E}\) a \(\mathrm{d}\vec{r\,}\) jsou tedy rovnoběžné a jejich skalární součin je proto roven součinu jejich velikostí:

  \[ U\,=\,\int_\mathrm{a}^\mathrm{b} E\left(r\right)\,\mathrm{d}r\,=\,\frac{I}{4\pi \sigma}\int_\mathrm{a}^\mathrm{b} \frac{\mathrm{d}r}{r^2}\,=\,\frac{I}{4\pi \sigma}\,\left[\frac{-1}{r}\right]_\mathrm{a}^\mathrm{b}\,=\,\frac{I}{4\pi \sigma}\,\left(\frac{1}{a}\,-\,\frac{1}{b}\right)\,. \]

  Odpor materiálu získáme jako podíl napětí U mezi elektrodami a proudu I, který mezi elektrodami prochází:

  \[ R\,=\,\frac{U}{I}\,=\,\frac{\frac{I}{4\pi \sigma}\,\left(\frac{1}{a}\,-\,\frac{1}{b}\right)}{I}\,. \]

  Celkový elektrický odpor mezi kulovými elektrodami tedy vypočítáme podle vztahu:

  \[ R\,=\,\frac{1}{4\pi\sigma}\left(\frac{1}{a}\,-\,\frac{1}{b}\right) \] \[ R\,=\,\frac{1}{4\pi\sigma}\,\frac{b-a}{ab} \] \[ R\,=\,\frac{b-a}{4\pi\sigma ab}. \]

  Proud I procházející mezi elektrodami se rovná podílu napětí U a elektrického odporu R mezi elektrodami:

  \[ I\,=\,\frac{U}{R}\,=\,\frac{4\pi\sigma ab}{b-a}\,U\,. \]

• III. Nápovědy

• Nápověda 1

  Elektrické pole vytvořené mezi kulovými elektrodami se s časem nemění (je stacionární). Ve stacionární situaci můžeme použít formální podobnost se zákony elektrostatiky.

  Poznámka: Vysvětlení formální podobnosti se zákony elektrostatiky najdete v úloze Elektrický proud mezi válcovými elektrodami v oddíle III., Nápověda 1.

• Nápověda 2

  Uvědomte si nebo si vyhledejte, jak vypadá Gaussova věta elektrostatiky v integrálním tvaru.

• Řešení nápovědy 2

  Gaussova věta v integrálním tvaru:

  \[ \oint \vec{E}\cdot \mathrm{d}\vec{S}\,=\,\frac{Q}{\epsilon}\,. \]

  Značka \(\normalsize{\oint}\) vyjadřuje, že plošný integrál je počítán přes uzavřenou plochu, \(\vec{E}\) je intenzita elektrického pole, Q celkový náboj uzavřený uvnitř plochy S a ε je permitivita dané látky.

  Gaussova věta nám udává vztah mezi intenzitou elektrického pole a nábojem.

• Nápověda 3

  Pokud by mezi elektrodami nebyl vodič ale dielektrikum, jednalo by se vlastně o kondenzátor. Díky formální podobnosti se zákony elektrostatiky bude průběh intenzity elektrického pole úplně stejný. Elektrickou intenzitu v Gaussově větě tedy sice vyjádříme ve stacionárním případě, ale pro náboj Q si „půjčíme“ vztah ze statického případu.

  Velikost náboje proto vyjádříme pomocí kapacity kulových elektrod. Takto vyjádřenou velikost náboje dosadíme do Gaussovy věty elektrostatiky.

• Řešení nápovědy 3

  Vztah mezi velikostí náboje Q a rozdílem potenciálů U lze vyjádřit pomocí kapacity C kulových elektrod:

  \[ Q\,=\,CU\,. \]

  Kapacita C kulového kondenzátoru je dána vztahem:

  \[ C\,=\,\frac{4\pi \epsilon}{\frac{1}{a}\,-\,\frac{1}{b}}\,=\,\frac{4\pi\epsilon}{\frac{b-a}{ab}} \] \[ C\,=\,\frac{4\pi\epsilon ab}{b-a}\,, \]

  kde ε je permitivita prostředí a a, b jsou poloměry kulových ploch, které tvoří kondenzátor (a < b).

• Nápověda 4

  Uvědomte si, jak vypadá Ohmův zákon v diferenciálním tvaru.

  Poznámka: Ohmův zákon v diferenciálním tvaru naleznete v této úloze v oddíle II. Nápověda 1.

• III. Rozbor

  Odpor a proud mezi kulovými elektrodami vypočítáme za pomoci formální analogie s elektrostatickým polem.

  Budeme uvažovat, že elektrody jsou vnořeny do dielektrika o určité permitivitě. Na elektrody jsou přivedeny náboje stejné velikosti, ale opačného znamení tak, že udržují původní hodnoty potenciálů. Mezi elektrodami bude tedy stejný průběh elektrické intenzity. Pro vyjádření intenzity použijeme Gaussovu větu v integrálním tvaru.

  Do vyjádření intenzity dosadíme Ohmův zákon pro homogenní vodiče v diferenciálním tvaru. Tím získáme proud procházející mezi elektrodami v závislosti na velikosti náboje kulových elektrod. Elektrický náboj pak vyjádříme za pomoci kapacity kulového kondenzátoru.

  Odpor mezi kulovými elektrodami je podle Ohmova zákona roven podílu napětí mezi elektrodami a proudu, který mezi nimi protéká.

• III. Řešení

  Představme si, že mezi elektrodami je místo vodiče dielektrikum o permitivitě ε a je na ně přiveden náboj stejné velikosti Q, ale opačného znamení tak, že udržuje původní hodnoty potenciálů. V řešení využijeme toho, že průběh elektrické intenzity je stejný jak v tomto statickém případě, tak ve stacionárním případě, kdy mezi elektrodami protéká ustálený proud.

  Nejprve si napišme dva vztahy popisující kulový kondenzátor, které použijeme později. Mezi velikostí náboje Q, rozdílem potenciálů (tj. napětím U) a kapacitou C platí vztah:

  \[ Q\,=\,UC. \]

  Kapacita kulového kondenzátoru C je dána vztahem:

  \[ C\,=\,\frac{4\pi\epsilon}{\frac{1}{a}\,-\,\frac{1}{b}}\,=\,\frac{4\pi\epsilon ab}{b-a}\,, \tag{*}\]

  kde ε je permitivita prostředí a a, b jsou poloměry kulových elektrod, které tvoří kondenzátor, přičemž a < b.

  Pusťme se teď do vlastního řešení. Použijeme Gaussovu větu v integrálním tvaru:

  \[ \oint \vec{E}\cdot\mathrm{d}\vec{S}\,=\,\frac{Q}{\epsilon}\,, \]

  kde \(\vec{E}\) je intenzita elektrického pole, Q náboj přivedený na kulové elektrody povrchu S a ε je permitivita dané látky.

  Ohmův zákon pro homogenní vodiče v diferenciálním tvaru říká:

  \[ \vec{j}\,=\,\sigma \vec{E}, \]

  kde \(\vec{j}\) je hustota elektrického proudu a σ měrná elektrická vodivost.

  Celkový proud I procházející mezi elektrodami si vyjádříme pomocí hustoty proudu \(\vec{j\,}:\)

  \[ I\,=\,\oint \vec{j\,}\cdot\mathrm{d}\vec{S}, \]

  kam za hustotu proudu \(\vec{j\,}\) dosadíme z Ohmova zákona a dále použijeme pro úpravu Gaussovu větu:

  \[ I\,=\,\oint \sigma \vec{E}\cdot\mathrm{d}\vec{S}\,=\,\sigma\oint\vec{E}\cdot\mathrm{d}\vec{S}\,=\,\sigma\frac{Q}{\epsilon}\,. \]

  Za velikost náboje Q na jedné elektrodě dosadíme vyjádření náboje pomocí kapacity \(Q\,=\,CU\):

  \[ I\,=\,\sigma\frac{CU}{\epsilon}\,. \]

  Dosazením kapacity kulového kondenzátoru C, tj. vztahu (*), získáme vzorec pro výpočet celkového proudu, který prochází mezi elektrodami:

  \[ I\,=\,\sigma\frac{\frac{4\pi\epsilon ab U}{b-a}}{\epsilon} \] \[ I\,=\,\frac{4\pi\sigma ab}{b-a}\,U. \]

  Odpor mezi kulovými elektrodami vypočítáme jako podíl napětí U mezi elektrodami a proudu I, který mezi elektrodami prochází:

  \[ R\,=\,\frac{U}{I}\,=\,\frac{U}{\frac{4\pi\sigma ab}{b-a}\,U} \] \[ R\,=\,\frac{b-a}{4\pi\sigma ab}. \]

• b) Nápovědy

• Nápověda 1

  V předchozích částech řešení této úlohy jsme vypočítali odpor mezi dvěma kulovými vodiči o poloměru a a b (a < b):

  \[ R\,=\,\frac{b-a}{4\pi\sigma ab}\,=\,\frac{1}{4\pi\sigma}\left(\frac{1}{a}\,-\,\frac{1}{b}\right)\,. \]

  Uvědomte si, jak se tento odpor bude měnit, jestliže poloměr b vnějšího vodiče bude mnohokrát větší než poloměr a vnitřní sféry (tj. b >> a).

• Řešení nápovědy 1

  Jestliže poloměr b vnějšího vodiče bude mnohokrát větší než poloměr a vnitřní sféry (tj. b >> a), pak převrácená hodnota poloměru b bude mnohem menší než převrácená hodnota poloměru a, tedy \(\frac{1}{b}\,<<\,\frac{1}{a}\).

  Odpor prostředí mezi dvěma kulovými vodiči vypočítáme ze vztahu:

  \[ R\,=\,\frac{1}{4\pi\sigma}\left(\frac{1}{a}\,-\,\frac{1}{b}\right). \]

  Je-li b >> a, můžeme člen \(\frac{1}{b}\) zanedbat. Pro odpor prostředí tedy získáme vzorec:

  \[ R\,\approx\,\frac{1}{4\pi\sigma a}\,. \]

  K odporu prostředí mezi elektrodami tedy nejvíce přispívá materiál, který je soustředěn u povrchu sféry o poloměru a. Tento vztah tedy můžeme v prvním přiblížení považovat za odpor okolí kulové elektrody o poloměru a.

• Nápověda 2

  Abychom určili proud mezi dvěma kulovými elektrodami, které jsou ponořené hluboko v moři a jsou od sebe značně vzdálené, musíme určit odpor vody mezi nimi. Z předchozí nápovědy víme, že k odporu nejvíce přispívá materiál v těsném okolí elektrody, a také víme, jak ho spočítat. Odpor mezi oběma elektrodami můžeme tedy určit jako odpor dvou sériově zapojených „okolí elektrod“.

• b) Rozbor

  Předpokládejme, že máme dva soustředné kovové sférické vodiče poloměrů a a b, přičemž a << b. Díky této podmínce získáme z předchozích výsledků vzorec pro odpor okolí kulové elektrody o poloměru a.

  Proud tekoucí mezi dvěma kulovými elektrodami, které jsou ponořené hluboko v moři a jsou od sebe značně vzdálené, bude potom stejný jako proud, který protéká dvěma sériově spojenými rezistory, jejichž odpory odpovídají odporům okolí obou elektrod.

• b) Řešení

  V předchozích částech řešení této úlohy jsme vypočítali odpor mezi dvěma kulovými vodiči o poloměrech a a b (a < b):

  \[ R\,=\,\frac{b-a}{4\pi\sigma ab}\,=\,\frac{1}{4\pi\sigma}\left(\frac{1}{a}\,-\,\frac{1}{b}\right), \tag{**}\]

  kde σ je vodivost prostředí, v našem případě mořské vody.

  Pokud je b >> a, pak \(\frac{1}{b}\,<<\,\frac{1}{a}\). Člen \(\frac{1}{b}\) ve vztahu (**) můžeme tedy zanedbat. Pro odpor prostředí tím získáme vzorec:

  \[ R\,\approx\,\frac{1}{4\pi\sigma a}\,. \]

  Odpor prostředí je nejvíce soustředěn k povrchu sféry. Tento vztah tedy můžeme v prvním přiblížení považovat za odpor okolí kulové elektrody o poloměru a.

  Proud tekoucí mezi dvěma kulovými elektrodami, které jsou ponořené hluboko v moři a jsou od sebe značně vzdálené, bude stejný jako proud protékající dvěma sériově spojenými rezistory, jejichž odpory odpovídají odporům okolí daných elektrod. Celkový odpor tohoto sériového zapojení se tedy bude rovnat součtu těchto odporů:

  \[ R_\mathrm{celk}\,=\,2R\,\approx\,2\,\frac{1}{4\pi\sigma a}\,=\,\frac{1}{2\pi\sigma a}\,. \]

  Proud tekoucí mezi kulovými elektrodami vyjádříme jako podíl napětí U mezi elektrodami a celkového odporu elektrod R_celk. Tedy:

  \[ I\,\approx\,\frac{U}{R_\mathrm{celk}}\,=\,\frac{U}{\frac{1}{2\pi\sigma a}} \] \[ I\,\approx\,2\pi\sigma aU. \]

• Odpověď

  a) Elektrický odpor mezi soustřednými kulovými elektrodami o poloměrech a a b vypočítáme ze vztahu:

  \[ R\,=\,\frac{b-a}{4\pi\sigma ab}\,, \]

  pro proud procházející mezi těmito elektrodami platí:

  \[ I\,=\,\frac{4\pi\sigma ab}{b-a}\,U \,, \]

  kde σ je vodivost materiálu mezi elektrodami a U značí napětí mezi elektrodami.

  Poznámka: Všemi třemi způsoby řešení jsme získali stejný výsledek.

  b) Proud protékající mezi dvěma elektrodami o poloměrech a, které jsou ponořené hluboko v moři a jsou od sebe značně vzdáleny, určíme ze vztahu:

  \[ I\,=\,2\pi\sigma aU. \]

• Odkaz na podobné úlohy

  Zkuste si vyřešit úlohy Elektrický proud mezi válcovými elektrodami a Nehomogenní prostředí mezi válcovými elektrodami, ve kterých je také úkolem určit proud a odpor mezi dvěma elektrodami.