Výpočet velikosti proudů v obvodu se dvěma zdroji
Úloha číslo: 30
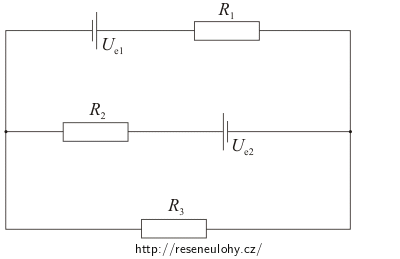
Na obrázku je nakresleno schéma obvodu se dvěma zdroji elektromotorického napětí Ue1, Ue2 a se třemi rezistory R1, R2, R3.
Určete, jaké proudy procházejí jednotlivými rezistory (jaká je jejich velikost a směr), jestliže:
| Ue1 = 2Ue2 |
| Ue2 = 20 V |
| R1 = R3 = 20 Ω |
| R2 = 30 Ω |
Nápověda
K řešení příkladu použijte Kirchhoffovy zákony.
Rozbor - postup řešení
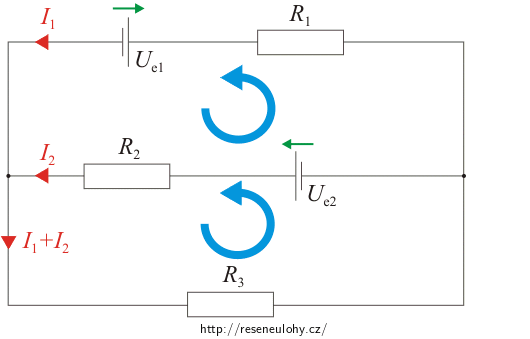
1. Do obrázku si vyznačíme směry elektromotorického napětí zdrojů (zelené šipky).
2. Zvolíme si a nakreslíme směry proudů (červené šipky). I. Kirchhoffův zákon říká, že proudy vstupující do uzlu se rovnají proudům, které z tohoto uzlu vytékají. Tento zákon můžeme aplikovat rovnou do obrázku.
3. Zvolíme si smyčky a jejich směry (modré šipky).
4. Sestavíme pro smyčky rovnice podle II. Kirchhoffova zákona.
5. Řešíme získané rovnice pro jednotlivé smyčky.
Podrobnější popis použití Kirchhoffových zákonů najdete u úlohy Použití Kirchhoffových zákonů pro řešení obvodu se dvěma zdroji.
Výpočet proudů I1 a I2
Pozn.: Začátek řešení úlohy je na obrázku v oddílu Rozbor.
Sestavíme si rovnice podle II. Kirchhoffova zákona:
\[R_1I_1-R_2I_2\,=\,-U_{e1}-U{e2}\tag{horní smyčka}\] \[R_2I_2+R_3(I_1+I_2)\,=\,U_{e2}\tag{dolní smyčka}\]Získali jsme soustavu dvou rovnic pro dvě neznámé I1, I2.
Do rovnic pro obě smyčky si dosadíme zadané hodnoty. Neznámé I1 a I2 představují proudy v ampérech. Aby byl zápis přehledný, dopíšeme jednotky až k výsledku řešení.
\[20I_1-30I_2\,=\,-2{\cdot} 20-20\] \[30I_2+20(I_1+I_2)\,=\,20\,.\]Tedy:
\[20I_1-30I_2\,=\,-60\] \[20I_1+50I_2\,=\,20\,.\]První rovnici odečteme od druhé:
\[\left(20I_1+50I_2\right)-\left(20I_1-30I_2\right)\,=\,20-\left(-60\right)\] \[80I_2\,=\,80\] \[I_2\,=\,1{,}0\,\mathrm{A}\,.\]Nyní už známe velikost proudu I2, takže z rovnice
\[20I_1+50I_2\,=\,20\]vypočítáme proud I1:
\[20I_1+50\,=\,20\] \[20I_1\,=\,-30\] \[I_1\,=\,-1{,}5\,\mathrm{A}\,.\]Nyní ještě spočítáme proud procházející rezistorem R3:
\[I_1+I_2\,=\,-0{,}5\,\mathrm{A}\,.\]Odpověď
Rezistorem R1 prochází proud 1,5 A. Jeho směr je opačný než směr, který jsme si zvolili do obrázku.
Rezistorem R2 prochází proud 1,0 A. Jeho směr odpovídá směru, který jsme si zvolili do obrázku.
Rezistorem R3 prochází proud 0,5 A. Jeho směr je opačný než směr, který jsme si zvolili do obrázku.
Poznámka - obecný výpočet proudů I1, I2
Zkusme úlohu vyřešit i obecně. Máme následující dvě rovnice a chceme vyjádřit neznámé I1 a I2:
\[R_1I_1-R_2I_2\,=\,-U_\mathrm{e1}-U_\mathrm{e2}\] \[R_2I_2+R_3\left(I_1+I_2\right)\,=\,U_\mathrm{e2}\,.\]Z první rovnice si vyjádříme proud I2:
\[I_2\,=\,\frac{R_1I_1+U_\mathrm{e1}+U_\mathrm{e2}}{R_2}\,.\tag{*}\]Druhou rovnici si upravíme tak, abychom měli u sebe členy s I1 a členy s I2:
\[\left(R_2+R_3\right)I_2+R_3I_1\,=\,U_\mathrm{e2}\,.\]A za I2 dosadíme:
\[\left(R_2+R_3\right)\frac{R_1I_1+U_\mathrm{e1}+U_\mathrm{e2}}{R_2}+R_3I_1\,=\,U_\mathrm{e2}\,.\]Nyní celou rovnici vynásobíme R2:
\[\left(R_2+R_3\right)\left(R_1I_1+U_\mathrm{e1}+U_\mathrm{e2}\right)+R_2R_3I_1\,=\,R_2U_\mathrm{e2}\,.\]Dalšími úpravami si z rovnice postupně vyjádříme I1:
\[\left(R_1R_2+R_1R_3+R_2R_3\right)I_1+\left(R_2+R_3\right) \left(U_\mathrm{e1}+U_\mathrm{e2}\right)\,=\,R_2U_\mathrm{e2}\] \[\left(R_1R_2+R_1R_3+R_2R_3\right)I_1\,=\,R_2U_\mathrm{e2}- \left(R_2+R_3\right)\left(U_\mathrm{e1}+U_\mathrm{e2}\right)\] \[\left(R_1R_2+R_1R_3+R_2R_3\right)I_1 \,=\,-\left(R_2+R_3\right)U_\mathrm{e1}-R_3U_\mathrm{e2}\] \[I_1\,=\,-\frac{\left(R_2+R_3\right)U_\mathrm{e1}+R_3U_\mathrm{e2}} {R_1R_2+R_1R_3+R_2R_3}\,.\]Proud I2 vypočítáme dosazením za I1 do vztahu (*).
Vztahy můžeme zjednodušit dosazením Ue1 = 2Ue2 a R1 = R3:
\[I_1\,=\,-\frac{\left(R_2+R_3\right)2U_\mathrm{e2}+R_3U_\mathrm{e2}} {R_3R_2+R_3R_3+R_2R_3}\] \[I_2\,=\,\frac{R_1I_1+2U_\mathrm{e2}+U_{e2}}{R_2}\,.\]Výsledné obecné vztahy:
\[I_1\,=\,-\frac{\left(2R_2+3R_3\right)U_\mathrm{e2}} {{R_3}^2+2R_2R_3}\] \[I_2\,=\,\frac{R_3I_1+3U_\mathrm{e2}}{R_2}\]



