Ampérova křivka
Úloha číslo: 168
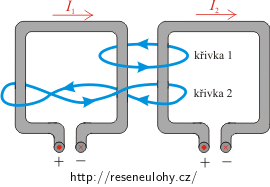
Dvěma vodivými smyčkami čtvercového tvaru protékají proudy 5 A a 3 A. Určete hodnotu integrálu \(\oint\vec{B}\cdot \,\mathrm{d}\vec{l}\) pro obě uzavřené křivky vyznačené na obrázku.
Nápověda
Provést přímou integraci by vyžadovalo znát průběh magnetického pole v okolí dané křivky, což by bylo dost složité určit. Proto pro určení integrálu vyjděte z Ampérova zákona, kde za proud uvažujte celkový proud procházející zvolenou křivkou.
Rozbor
Nejdříve určíme integrál pro křivku 1. Tato křivka obepíná dva vodiče, jejichž směry proudů se liší. Pro určení integrálu vyjdeme z Ampérova zákona, kde proud na pravé straně rovnice představuje celkový proud, který plochou ohraničenou Ampérovou křivkou, prochází. Znaménko každého z proudů, které vytvářejí celkový proud, určuje pravidlo pravé ruky, které říká: Ohněte prsty pravé ruky kolem Ampérovy křivky tak, aby ukazovaly ve směru její orientace, potom proudu, který teče ve směru vztyčeného palce, přiřadíme kladné znaménko a proudu tekoucímu opačně znaménko záporné.
Podobně budeme postupovat i u druhé křivky. Zde si musíme dát pozor při určení směru proudu na to, že smyčka je „překřížena“ a její orientaci vždy určovat pomocí té části, která obepíná daný vodič.
Řešení
Pro určení integrálu vyjdeme z Ampérova zákona, jehož tvar je:
\[\oint \vec{B}\cdot \,\mathrm{d}\vec{l}=\mu_\mathrm{0} I_\mathrm{c},\]kde Ic značí celkový proud uzavřený Ampérovou smyčkou délky l. Vidíme, že levá strana Ampérova zákona přesně odpovídá hledanému integrálu.
Celkový proud odpovídá součtu proudů obepnutých proudovou křivkou. V případě křivky 1 jsou to dva vodiče s různými směry proudů. Znaménko každého z proudů určíme pomocí pravidla pravé ruky. Při zvolené orientaci křivky platí pro celkový proud:
\[I_\mathrm{c}=-I_1+I_2.\]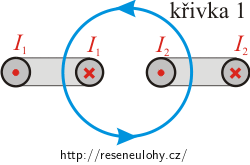
Ampérův zákon pro křivku 1 můžeme přepsat do tvaru:
\[\oint_1 \vec{B}\,\cdot \,\mathrm{d}\vec{l}=\mu_\mathrm{0}(-I_1+I_2).\]Křivka 2 obepíná tři vodiče s proudy. Znaménko každého z proudů určíme také pomocí pravidla pravé ruky. Zde si musíme dávat pozor na orientaci křivky, která se různě přetáčí.
Pro celkový proud obepnutý křivkou 2 dostáváme:
\[I_\mathrm{c}=-I_1-I_1-I_2.\]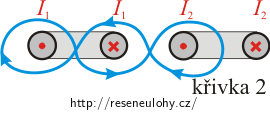
Ampérův zákon pro křivku 2 má pak tvar:
\[\oint_2 \vec{B}\,\cdot \,\mathrm{d}\vec{l}=\mu_\mathrm{0}(-2I_1-I_2).\]Zápis a číselné dosazení
\(I_1=5\,\mathrm{A}\) proud tekoucí první smyčkou \(I_2=3\,\mathrm{A}\) proud tekoucí druhou smyčkou \(\oint_1 \vec{B}\,\cdot \,\mathrm{d}\vec{l}=?\,\mathrm{Tm}\) hodnota, kterou máme určit pro první křivu \(\oint_2 \vec{B}\,\cdot \,\mathrm{d}\vec{l}=?\,\mathrm{Tm}\) hodnota, kterou máme určit pro druhou křivku Z tabulek: \(\mu_\mathrm{0}=4\pi\cdot 10^{-7}\,\mathrm{Hm^{-1}}\) permitivita vakua
\[\oint_1 \vec{B}\,\cdot \,\mathrm{d}\vec{l}=\mu_\mathrm{0}(-I_1+I_2)=4\pi\cdot 10^{-7}\cdot(-5+3)\,\mathrm{T\,m}=-8\pi\cdot 10^{-7}\,\mathrm{T\,m}\] \[\oint_2 \vec{B}\,\cdot \,\mathrm{d}\vec{l}=\mu_\mathrm{0}(-2I_1-I_2)=4\pi\cdot 10^{-7}\cdot(-10-3)\,\mathrm{T\,m}=-52\pi\cdot 10^{-7}\,\mathrm{T\,m}\]Odpověď
Pro křivku 1 je hodnota integrálu rovna: \[\oint_1 \vec{B}\cdot \,\mathrm{d}\vec{l}=-8\pi \cdot 10^{-7}\,\mathrm{T\,m}.\]
A pro křivku 2 platí: \[\oint_2 \vec{B}\cdot \,\mathrm{d}\vec{l}=-52\pi \cdot 10^{-7}\,\mathrm{T\,m}.\]


