Smyčka měnící svoji plochu
Úloha číslo: 2313
Čtvercová smyčka o hraně a je umístěna do homogenního magnetického pole, které míří směrem do nárysny. Na protilehlých vrcholech čtverce začne působit síla a během časového intervalu \(\Delta t\) deformuje čtverec v kosočtverec, jak je vidět na obrázku. Za předpokladu, že celkový odpor smyčky je R, spočítejte průměrný proud, který smyčkou tekl, a určete jeho směr.

Nápověda
Vodivá smyčka je deformována v magnetickém poli. Proč by měl smyčkou téci proud, když není připojená ke zdroji?
Nápověda − potřebné vztahy
Faradayův zákon elektromagnetické indukce říká: Změní-li se magnetický indukční tok plochou vodivé smyčky za dobu \(\Delta t\) o \(\Delta\Phi\), vzniká ve smyčce indukované elektromotorické napětí, jež je dáno vztahem
\[U_\mathrm{i} = - \frac{\Delta\Phi}{\Delta t}.\]Magnetický indukční tok plochou o obsahu S je v případě homogenního pole definován jako \(\Phi=BS\cos\alpha\), kde \(\alpha\) je úhel, který svírá normála plochy s vektorem magnetické indukce \(\vec{B}.\)
Indukuje-li se ve vodiči o odporu R elektromotorické napětí \(U_\mathrm{i}\), pak se indukovaný proud procházející vodičem spočítá pomocí Ohmova zákona:
\[I=\frac{U_\mathrm{i}}{R}.\]Obsah kosočtverce
Obsah kosočtverce spočítáme pomocí vzorce
\[S=av_\mathrm{a},\]kde a je strana kosočtverce a \(v_\mathrm{a}\) je výška na tuto stranu.
Řešení
Indukované napětí
Faradayův zákon elektromagnetické indukce má tvar
\[U_\mathrm{i}=-\frac{\Delta \Phi}{\Delta t},\tag{1}\]kde \(\frac{\Delta \Phi}{\Delta t}\) je průměrná změna magnetického indukčního toku.
Magnetický indukční tok smyčkou o obsahu S je v případě homogenního pole definován jako \(\Phi=BS\cos\alpha\), kde \(\alpha\) je úhel, který svírá normála smyčky s vektorem magnetické indukce \(\vec{B}.\) V našem případě je \(\cos\alpha=1\), jelikož magnetické indukční čáry a normála smyčky jsou rovnoběžné, tudíž \(\Phi=BS\). A díky tomu, že magnetické pole se v čase nemění, můžeme předchozí vztah upravit
\[U_\mathrm{i}=-B\frac{\Delta S}{\Delta t},\]kde \(\frac{\Delta S}{\Delta t}\) je průměrná změna obsahu čtverce.
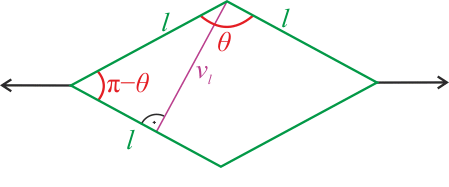
Při deformaci čtverce se mění jeho obsah. Vyjádřeme obsah kosočtverce v závislosti na úhlu \(\theta:\)
\[S=l v_l=l\thinspace l\sin(\pi-\theta)=l^2\sin\theta.\]Pozn.: Zde je nutné poznamenat, že vztah \(v_l=l\sin(\pi-\theta)\), platí pouze pro \(\theta \in \langle \frac{\pi}{2},\pi\rangle\). Což je v našem případě splněno, protože na počátku \(\theta = \frac{\pi}{2}\) a maximální úhel po zdeformování je zjevně \(\theta = \pi.\)
Změna obsahu, tj. rozdíl obsahu čtverce a kosočtverce, je
\[\Delta S=l^2\sin\theta-l^2=l^2(\sin\theta-1).\]Poslední vztah dosaďme do (1) a dostaneme průměrné indukované napětí \(U_\mathrm{i}\):
\[U_\mathrm{i}=-B\frac{l^2(\sin\theta-1)}{\Delta t}=\frac{Bl^2(1-\sin\theta)}{\Delta t}.\]Indukovaný proud
Průměrný indukovaný proud dopočítáme z Ohmova zákona:
\[I=\frac{U_\mathrm{i}}{R}=\frac{Bl^2(1-\sin\theta)}{R \Delta t}.\]Směr proudu
Lenzův zákon říká, že indukovaný proud má takový směr, aby svým magnetickým polem působil proti změně magnetického indukčního toku, která je jeho příčinou.
Obsah smyčky se zmenšuje, takže se zmenšuje magnetický tok. Indukovaný proud musí tedy téci takovým směrem, aby zvětšoval magnetický indukční tok smyčkou, tj. jeho pole musí také směřovat do obrázku. Z Ampérova pravidla dostáváme, že proud musí téci po směru chodu hodinových ručiček.
Ověřme předchozí závěr ještě zamyšlením nad sílami, které na vodič působí. Proud teče po směru hodinových ručiček, zakreslíme síly, které působí na jednotlivé vodiče tvořící rovnoběžník. Využijeme Flemingovo pravidlo levé ruky: „Položíme-li otevřenou levou ruku dlaní nahoru tak, že prsty ukazují směr proudu vodičem a indukční čáry magnetického pole vstupují do dlaně, pak bude palec ukazovat směr síly, kterou magnetické pole na vodič působí.“
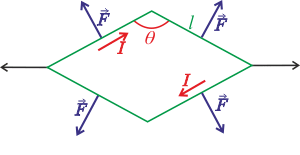
Jak ukazuje obrázek, síly působí proti deformaci, a tudíž i proti změně magnetického indukčního toku. Směr indukovaného proudu můžeme určit i pomocí působící síly.
Odpověď
Proud indukovaný deformací ve smyčce teče ve směru hodinových ručiček a má průměrnou velikost
\[I=B\frac{l^2(1-\sin\theta)}{R \Delta t}.\]Komentář − průběh proudu
Zamysleme se nyní také nad časovým průběhem proudu. Určili jsme průměrnou hodnotu proudu, ale neřešili jsme, zda má stálou či v čase proměnnou velikost. Časový průběh bychom dostali, pokud bychom ve Faradayově zákoně uvažovali časovou derivaci magnetického toku místo pouhého podílu rozdílů, tj.
\[U_\mathrm{i}=Bl^2\frac{\mathrm{d}(1-\sin\theta(t))}{\mathrm{d} t}=-Bl^2\frac{\mathrm{d}\sin\theta(t)}{\mathrm{d} t},\]kde \(\theta(t)\) vyjadřuje, jak se v čase měnila velikost úhlu \(\theta\). Z toho plyne, že průběh proudu závisí na tom, jakým způsobem je čtverec deformován. Bude tedy rozdíl, pokud bude úhel deformován rovnoměrně nebo nerovnoměrně (např. pokud se bude rychlost deformace zvyšovat). Ze zadaných údajů však průběh deformace určit nemůžeme, tedy nemůžeme určit ani časový průběh proudu.

