Tlumivka
Úloha číslo: 159
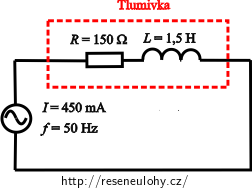
Do obvodu střídavého proudu o frekvenci 50 Hz je zapojena tlumivka o indukčnosti 1,5 H a odporu 150 Ω.
a) Určete napětí na tlumivce a fázový rozdíl mezi napětím a proudem, jestliže tlumivkou prochází proud 450 mA.
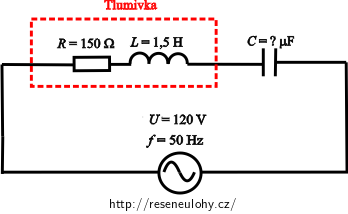
b) Jakou kapacitu musí mít kondenzátor připojený sériově k tlumivce, aby fázový rozdíl napětí a proudu byl nulový? Jaký proud bude procházet v tomto případě obvodem při napětí 120 V?
Zápis
Ze zadání známe (pro oba úkoly stejné):
Frekvenci na zdroji: f = 50 Hz Indukčnost tlumivky: L = 1,5 H Odpor tlumivky: R = 150 Ω a) Dále známe:
Proud tlumivkou: I = 450 mA Chceme určit:
Napětí na tlumivce: U = ? (V) Fázový rozdíl mezi napětím a proudem: φ = ? (°) b) Dále známe:
Napětí na zdroji: U = 120 V Fázový rozdíl mezi napětím a proudem: φ = 0° Chceme určit:
Kapacitu kondenzátoru připojeného k tlumivce sériově: C = ? (F) Proud tlumivkou: I = ? (A) Nápověda
Pomocí Ohmova zákona pro střídavý proud vyjádříme napětí a proud.
Pro vyjádření fázového posunu budeme potřebovat vzorec, který vyjadřuje jeho tangens v závislosti na impedancích. Odvození tohoto vztahu je uvedeno v úloze Sériový RLC obvod.
Nápověda - kdy nastává nulový fázový posun
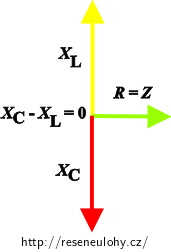
Fázový diagram ukazuje, že je-li hodnota kapacitance s induktancí stejně velká, potom je fázový posun nulový.
Rozbor
a) Máme-li v obvodu zařazenou cívku a rezistor, proud a napětí budou vzájemně fázově posunuté. Fázový posun vyjádříme z fázorového diagramu na obrázku nebo využijeme vzorce, které jsou odvozeny v úloze Sériový RLC obvod.
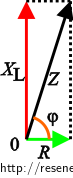
Napětí na tlumivce potom získáme z Ohmova zákona, kde impedanci máme tvořenou z rezistance a induktance.
b) Nejdříve máme vyjádřit velikost kapacity kondenzátoru, který je připojen k tlumivce sériově. Velikost kapacity kondenzátoru má být taková, aby fázový rozdíl mezi napětím a proudem byl nulový. Je-li napětí a proud ve fázi, musí být kapacitance a induktance stejně velké. To lze odvodit z fázorového diagramu nebo k tomu dojdeme výpočtem.

a) Řešení
Napětí na tlumivce:
Ohmův zákon pro střídavé napětí je:
\[U=IZ=I \sqrt{R^2+X_\mathrm{L}^2}=I \sqrt{R^2+\left(\omega L\right)^2}=I \sqrt{R^2+\left(2 \pi f L\right)^2}.\]Po dosazení dostáváme:
\[U=450{\cdot} 10^{-3}\cdot \sqrt{150^2+\left(2\cdot \pi \cdot 50 {\cdot} 1{,}5\right)^2}\, \mathrm V \dot{=}\,223\, \mathrm V.\]Fázový posun mezi napětím a proudem:
Fázový posun vyjádříme pomocí vztahu:
\[\mathrm{tg}\, \varphi = \frac{X_\mathrm{L}}{R}=\frac{\omega L}{R}=\frac{2 \pi fL}{R}.\]Dosadíme a vyjádříme φ:
\[ \mathrm{tg}\, \varphi = \left(\frac{2 \pi fL}{R}\right)=\left(\frac{2 \pi \cdot 50 {\cdot} 1{,}5}{150}\right)\,\dot{=}\,3{,}14, \] \[ \varphi\,\dot{=}\,72 ^{\circ}. \]b) Řešení
Kapacita kondenzátoru:
Aby fázový posun byl nulový, musí platit: φ = 0 => tg φ = 0.
Pro fázový posun v sériovém RLC obvodu platí vztah:
\[\textrm{tg} \varphi = \frac{X_\mathrm{L} - X_\mathrm{C}}{R}.\]Řešíme rovnici — za tangens dosadíme nulu a vyjádříme kapacitu kondenzátoru:
\[ 0 = X_\mathrm{L} - X_\mathrm{C},\] \[ X_\mathrm{C}=X_\mathrm{L}.\]K tomuto vztahu se můžeme také dostat přímo pomocí fázorového diagramu (je uveden v části rozbor):
\[ \frac{1}{\omega C} = \omega L,\] \[ \omega C = \frac{1}{\omega L},\] \[ C = \frac{1}{\omega^2 L}=\frac{1}{(2 \pi f)^2 L}.\]Po dosazení dostáváme:
\[ C = \frac{1}{(2 \pi \cdot 50)^2 1{,}5}\,\mathrm F,\] \[ C \,\dot{=}\,6{,}8 {\cdot} 10^{-6} \,\mathrm F=6{,}8\,\mathrm {\mu F}. \]Proud v obvodu při napětí 120 V:
Z Ohmova zákona vyplývá:
\[I=\frac{U}{Z}=\frac{U}{\sqrt{R^2+(X_\mathrm{L}-X_\mathrm{C})^2}}=\frac{U}{\sqrt{R^2-0}}=\frac{U}{R}. \]Po dosazení dostáváme:
\[I=\frac{120}{150}\,\mathrm A, \] \[I = 0{,}8\,\mathrm A.\]Odpověď
Bude-li tlumivkou procházet proud 450 mA, pak na ní naměříme napětí přibližně 223 V. Velikost fázového posunu mezi napětím a proudem φ bude pro tento případ asi 72°.
Připojíme-li kondenzátor k tlumivce sériově tak, aby fázový posun mezi napětím a proudem byl nulový, pak musí být velikost kapacity kondenzátoru rovna přibližně 6,8 μF. Proud protékající tímto obvodem při napětí 120 V bude roven 0,8 A.

