Elektrické kyvadélko v poli nabité koule (velká výchylka)

Úloha číslo: 153

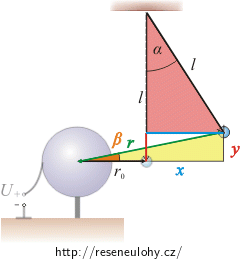
Ve vzdálenosti r₀ = 5 cm od středu vodivé koule o poloměru R = 2 cm je na vlákně délky l = 12 cm zavěšena malá kulička elektrického kyvadélka o hmotnosti m = 0,6 g.

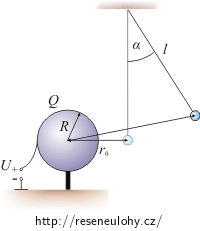
Kouli připojíme ke kladné svorce zdroje o napětí U = 22 kV, druhou svorku zdroje uzemníme. Na kuličku přeneseme neznámý náboj q. Kulička se působením elektrické síly vychýlí od svislého směru o úhel α = 25°. Náboje jsou souhlasné, a proto se odpuzují.

a) Jak velká elektrická síla působí na kuličku kyvadélka a jak velkou silou napíná kulička vlákno?

b) Jak velký náboj Q bude na kouli, když ji připojíme ke zdroji napětí? Jak velký náboj q bude na kuličce kyvadélka?

Pozn.: Sloupek, na kterém stojí koule, a vlákno závěsu kuličky jsou nevodivé.

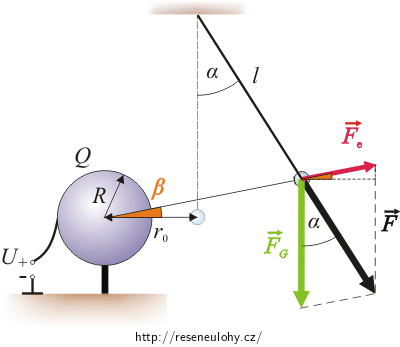
Obrázek působících sil
Nápověda

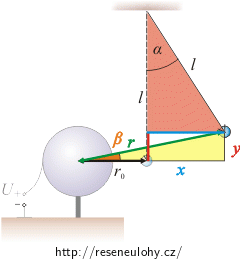
I když to zatím není ze zadání jasné, budeme pro další výpočty potřebovat úhel β. Vyjádříme ho pomocí goniometrických funkcí.
a) Nápověda: Vyjádření elektrické síly

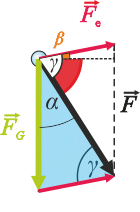
Zaměřte se na modrý trojúhelník.

Využijte sinové věty a vyjádřete poměr elektrické a tíhové síly.

Poznámka:

Sinová věta je uvedena v části Použité matematické vzorce.
Výpočet úhlu β

Pro další výpočty potřebujeme znát úhel β. Pro přehlednost ho spočítáme v této samostatné části a jeho číselnou hodnotu dosadíme do dalších výpočtů.

Úhel β budeme vyjadřovat ze žlutého pravoúhlého trojúhelníka:
\[\mathrm{tg}\,\beta \,=\,\frac{y}{r_0+x}.\tag{1}\]
Vzdálenosti x a y vypočítáme z červeného trojúhelníka také pomocí goniometrických funkcí:
\[x\,=\,l\sin\alpha,\] \[y\,=\,l-l\cos\alpha\,=\,l\left(1-\cos\alpha\right)\,\]
a dosadíme do vzorce (1):
\[\mathrm{tg}\,\beta \,=\,\frac{l\left(1-\cos\alpha\right)}{r_0+l\sin\alpha}.\]
a) Výpočet elektrické síly

Na kuličku kyvadélka působí tíhová síla \(\vec{F}_\mathrm{G}\) a odpudivá elektrická síla \(\vec{F}_\mathrm{e}\). Výslednicí těchto dvou sil je síla \(\vec{F}\), kterou kulička napíná provázek.

Elektrickou sílu vypočteme pomocí sinové věty z modrého trojúhelníka:
\[\frac{F_\mathrm{e}}{F_\mathrm{G}}\,=\,\frac{\sin \alpha}{\sin\gamma},\] \[F_\mathrm{e}\,=\,\frac{F_\mathrm{G}\,\sin \alpha}{\sin\gamma}.\tag{*}\]
Nyní si vyjádříme úhel γ pomocí známých úhlů α a β. Na obrázku vidíme dva shodné trojúhelníky (modrý a bílý). Úhel γ je také v bílém trojúhelníku a můžeme ho zapsat jako součet červeného úhlu 90° − α a úhlu β:

γ = 90° – α + β.

Úhel β jsme vypočítali v samostatné části (Výpočet úhlu β).

Úhel γ dosadíme do vzorce (*) a vzorec upravíme:
\[F_\mathrm{e}\,=\,\frac{F_\mathrm{G}\,\sin \alpha}{\sin\left(90^{\circ}-\alpha+\beta\right)}\,=\,\frac{F_\mathrm{G}\,\sin \alpha}{\sin\left(90^{\circ}-\left(\alpha-\beta\right)\right)}\] \[F_\mathrm{e}\,=\,\frac{F_\mathrm{G}\,\sin \alpha}{\cos\left(\alpha-\beta\right)}.\]
Zbývá už jen dosadit za tíhovou sílu F_G = mg:
\[F_\mathrm{e}\,=\,\frac{mg\,\sin \alpha}{\cos\left(\alpha-\beta\right)}.\]
a) Nápověda: Vyjádření síly, kterou kulička napíná provázek

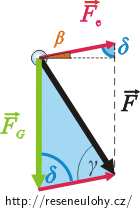
Z modrého trojúhelníka vyjádřete pomocí sinové věty poměr síly, kterou kulička napíná provázek, a tíhové síly.

Poznámka:

Sinová věta je uvedena v části Použité matematické vzorce.
a) Výpočet síly, kterou kulička napíná provázek

Sílu \(\vec{F}\), kterou kulička kyvadélka napíná provázek, spočítáme podobně jako elektrickou sílu pomocí sinové věty:
\[\frac{F}{F_\mathrm{G}}\,=\,\frac{\sin \delta}{\sin\gamma},\] \[F\,=\,\frac{F_\mathrm{G}\,\sin \delta}{\sin\gamma}.\]
Do vzorce dosadíme vyjádření úhlů γ a δ pomocí známých úhlů α a β.

Úhel γ jsme si vyjádřili v části Výpočet elektrické síly:

γ = 90° – α + β.

Úhel δ vyjádříme pomocí úhlu β (viz obrázek):

δ = 90° – β ,
\[F\,=\,\frac{F_G\,\sin \left(90^{\circ}-\beta\right)}{\sin\left(90^{\circ}-\alpha+\beta\right)}.\]
Čitatele a jmenovatele zlomku upravíme:
\[F\,=\,\frac{F_G\,\cos \beta}{\cos\left(\alpha-\beta\right)}.\]
Dosadíme za tíhovou sílu F_G = mg a získáme vztah pro výpočet síly F, kterou kulička napíná provázek:
\[F\,=\,\frac{mg\,\cos\beta}{\cos\left(\alpha-\beta\right)}.\]
b) Nápověda: Výpočet náboje na kouli a na kuličce kyvadélka
Výpočet náboje na kouli:

Koule je vodivá, proto se na ni bude přesouvat náboj ze zdroje napětí až do doby, než potenciál na povrchu koule bude stejný jako potenciál zdroje.

Výpočet náboje na kuličce kyvadélka:

K výpočtu náboje na kuličce využijte vypočítanou elektrickou sílu a Coulombův zákon.
b) Rozbor: Výpočet náboje na kouli a na kuličce kyvadélka
Potenciál na povrchu vodivé koule je stejný jako potenciál zdroje napětí. Pokud by byly potenciály různé, začne se náboj ze zdroje přesouvat na kouli (nebo naopak). Náboj by se přesouval až do doby než by se oba potenciály vyrovnaly.

Jedna svorka zdroje napětí je uzemněná, a proto je napětí na zdroji stejné jako potenciál neuzemněné svorky. Potenciál v okolí koule nabité na povrchu je stejný jako potenciál v okolí bodového náboje (je přímo úměrný náboji na kouli a nepřímo úměrný vzdálenosti od středu koule).

Na kuličku kyvadélka působí podle Coulombova zákona elektrická síla, která závisí přímo úměrně na náboji kuličky a koule a nepřímo úměrně na druhé mocnině vzdálenosti kuličky od koule. Pokud si vyjádříme vzdálenost středů kuličky a koule, můžeme z Coulombova zákona určit náboj kuličky.
b) Výpočet náboje na kouli
Koule je vodivá, proto veškerý volný elektrický náboj bude na jejím povrchu.

Pro potenciál na povrchu nabité koule platí stejný vztah jako pro potenciál v okolí bodového náboje:
\[\varphi\,=\,\frac{1}{4\pi\varepsilon_0}\,\frac{Q}{R}.\]
Potenciál na povrchu koule je roven napětí, ke kterému jsme kouli připojili, protože pokud by byl potenciál různý, náboj by se přesouval ze zdroje na kouli (nebo obráceně), dokud by se potenciály nevyrovnaly:
\[U\,=\,\varphi\,=\,\frac{1}{4\pi\varepsilon_0}\,\frac{Q}{R}.\]
Nyní stačí jen vyjádřit hledaný náboj Q:
\[Q\,=\,4\pi\varepsilon_0 U R. \tag{**}\]
b) Výpočet náboje na kuličce kyvadélka
Náboj, který jsme přenesli na kuličku kyvadélka, můžeme vypočítat z Coulombova zákona:
\[F_\mathrm{e}\,=\,\frac{1}{4\pi\epsilon_0} \,\frac{Qq}{r^2}.\]
Vyjádříme hledaný náboj q:
\[q\,=\,\frac{4\pi\varepsilon_0 F_\mathrm{e} r^2 } {Q}.\]
Dosadíme za náboj Q ze vzorce (**)
\[Q\,=\,4\pi\varepsilon_0 U R \,,\]
který jsme si vyjádřili v předchozí části úlohy (Výpočet náboje na kouli):

\[q\,=\,\frac{4\pi\varepsilon_0 F_\mathrm{e} r^2 } {4\pi\varepsilon_0 U R}\,=\,\frac{F_\mathrm{e} r^2 } {U R}.\]
Vzdálenost r vypočítáme pomocí žlutého trojúhelníka:
\[\sin\beta\,=\,\frac{y}{r},\] \[r\,=\,\frac{y}{\sin\beta}\,=\,\frac{l\left(1-\cos\alpha\right)}{\sin\beta}\]
a dosadíme do vzorce pro výpočet náboje q:
\[q\,=\,\frac{F_\mathrm{e} l^2\left(1-\cos\alpha\right)^2 } { U R\sin^2\beta}.\]

Do vztahu ještě dosadíme elektrickou sílu \(F_\mathrm{e}\,=\,\frac{mg\,\sin \alpha}{\cos\left(\alpha-\beta\right)}\), kterou jsme si spočítali v části Výpočet elektrické síly:
\[q\,=\,\frac { mg l^2\left(1-\cos\alpha\right)^2\sin \alpha } { U R\cos\left(\alpha-\beta\right)\sin^2\beta}.\]

Zápis a číselný výpočet

U = 22 kV = 2,2·10⁴ V	F_e = ? (N)
m = 0,6 g = 6·10⁻⁴ kg	F = ? (N)
l = 12 cm = 0,12 m	Q = ? (C)
R = 2 cm = 2·10⁻² m	q = ? (C)
r₀ = 5 cm = 5·10⁻² m	Z tabulek:
α = 25°	g = 9,8 ms⁻²
	ε₀ = 8,85·10⁻¹² C²N⁻¹m⁻²

Výpočet úhlu β: \[\mathrm{tg}\,\beta \,=\,\frac{l\left(1-\cos\alpha\right)}{r_0+l\sin\alpha}\,=\,\frac{0{,}12\,\cdot\left(1-\cos\, 25^\circ\right)}{0{,}05 \,+\,0{,}12\cdot\sin\, 25^\circ}\] \[\beta \,=\,6{,}37^\circ\] Výpočet elektrické síly: \[F_\mathrm{e}\,=\,\frac{mg\,\sin \alpha}{\cos\left(\alpha-\beta\right)} \,=\,\frac{6 {\cdot} 10^{-4} \cdot 9{,}8\cdot\,\sin 25^\circ}{\cos\left(25^\circ-6{,}37^\circ\right)}\,\mathrm{N}\,=\,2{,}6 {\cdot} 10^{-3}\,\mathrm{N} \] Výpočet síly provázku: \[F \,=\,\frac{mg\,\cos\beta}{\cos\left(\alpha-\beta\right)}\,=\,\frac{6 {\cdot} 10^{-4}\cdot 9{,}8\cdot\,\cos 6{,}37^\circ}{\cos\left(25^\circ-6{,}37^\circ\right)}\,\mathrm{N}\,=\,6{,}2 {\cdot} 10^{-3}\,\mathrm{N}\] Výpočet náboje na kouli: \[Q\,=\,4\pi\varepsilon_0 U R \, =\,4\pi\cdot 8{,}85 {\cdot} 10^{-12}\,\cdot\,2{,}2{\cdot} 10^{4}\,\cdot\, 2{\cdot} 10^{-2}\,\mathrm{C}\] \[Q\,=\,4{,}9{\cdot} 10^{-8}\,\mathrm{C}\] Výpočet náboje na kuličce kyvadélka: \[q\,=\,\frac { mgl^2\left(1-\cos\alpha\right)^2 \sin \alpha} { U R\cos\left(\alpha-\beta\right)\sin^2\beta} \] \[q\,=\,\frac { 6 {\cdot} 10^{-4}\,\cdot 9{,}8\, \cdot 0{,}12^2\cdot\left(1-\cos25^\circ\right)^2\sin 25^\circ } { 2{,}2{\cdot} 10^{4}\,\cdot\, 2{\cdot} 10^{-2}\cdot\cos\left(25^\circ-6{,}37^\circ\right)\cdot\sin^2 6{,}37^\circ}\,\mathrm{C}\,=\,6{,}1{\cdot} 10^{-8}\,\mathrm{C}\]

Odpověď
Na kuličku kyvadélka působí elektrická síla
\[F_\mathrm{e}\,=\,\frac{mg\,\sin \alpha}{\cos\left(\alpha-\beta\right)}\,=\,2{,}6 {\cdot} 10^{-3}\,\mathrm{N}\]
a kulička zároveň napíná vlákno silou
\[F \,=\,\frac{mg\,\cos\beta}{\cos\left(\alpha-\beta\right)}\,=\,6{,}2 {\cdot} 10^{-3}\,\mathrm{N}\,.\]
Po připojení zdroje se na kouli náboj objeví náboj
\[Q\,=\,4\pi\epsilon_0 U R \,=\,\,4{,}9{\cdot} 10^{-8}\,\mathrm{C}\,. \]
Zelektrovanou tyčí jsme na kuličku kyvadélka přenesli náboj
\[q\,=\,\frac { mgl^2\left(1-\cos\alpha\right)^2 \sin\alpha} { U R\cos\left(\alpha-\beta\right)\sin^2\beta}\,=\,6{,}1{\cdot} 10^{-8}\,\mathrm{C}\,.\]
Použité matematické vzorce
Mezi goniometrickými funkcemi platí vztah:
\[\sin {\left(90^\circ - \varphi\right)}\,=\, \cos \varphi. \]
V úloze jsme tento vztah využili v částech Výpočet elektrické síly a Výpočet síly, kterou kulička napíná provázek:
\[\sin {\left(90^\circ - \alpha+\beta\right)}\,=\,\sin {\left(90^\circ -\left( \alpha-\beta\right)\right)}\,=\, \cos{\left( \alpha - \beta \right)}.\]
Sinová věta:

Poměr délek stran trojúhelníku se rovná poměru sinů velikostí jim protilehlých úhlů:
\[\frac{a}{b}\,=\,\frac{sin\alpha}{sin\beta}.\]
Odkaz na jednodušší úlohu
Pokud by se kulička vychýlila pouze o malý úhel, mohli bychom úhel β zanedbat. Tento případ je vyřešen v úloze Elektrické kyvadélko v poli nabité koule (malá výchylka).