Cívka v obvodech s různými druhy napětí
Úloha číslo: 494
Připojíme-li cívku na stejnosměrné napětí 24 V, protéká jí proud 0,10 A. Připojíme-li stejnou cívku na střídavé napětí o efektivní hodnotě 24 V s frekvencí 50 Hz, protéká jí proud s efektivní hodnotou 50 mA. Určete:
a) elektrický odpor cívky,
b) impedanci cívky v druhém zapojení,
c) induktanci cívky v druhém zapojení a její indukčnost,
d) fázový posun mezi střídavým napětím a proudem cívkou pro daná zapojení.
Nápověda
K určení elektrického odporu je vhodné použít případ, kdy cívkou protéká stejnosměrný proud, protože její indukčnost se při časově neproměnném napětí neprojeví, a tudíž ji můžeme zanedbat. Výpočet elektrického odporu provedeme pomocí Ohmova zákona.
Impedance obvodu se projeví při zapojení cívky do obvodu se střídavým napětím, získáme ji pomocí Ohmova zákona. Induktanci cívky, její indukčnost a fázový posun mezi střídavým napětím a proudem lze odvodit pomocí fázorového diagramu.
Rozbor
Pro nalezení odporu cívky použijeme Ohmův zákon pro obvod se stejnosměrným napětím. Pro výpočet celkové impedance použijeme Ohmův zákon pro obvod se střídavým napětím.
Dále si nakreslíme fázorový diagram, ze kterého odvodíme vztah jak pro induktanci cívky, tak i pro fázový posun mezi napětím a proudem.
Indukčnost cívky určíme z její induktance.
Řešení
a) Elektrický odpor cívky R získáme pomocí Ohmova zákona pro obvod se stejnosměrným proudem
\[ R = \frac{U_1}{I_1}, \]kde U1 je stejnosměrné napětí zdroje a I1 je proud tekoucí cívkou při tomto napětí.
b) Celkovou impedanci cívky Z získáme pomocí Ohmova zákona pro obvod se střídavým proudem
\[ Z = \frac{U_2}{I_2}, \]kde U2 je efektivní hodnota střídavého napětí zdroje a I2 je efektivní hodnota proudu tekoucího cívkou při tomto napětí.
c) Vztah pro induktanci cívky XL odvodíme z fázorového diagramu překresleného pomocí impedancí:
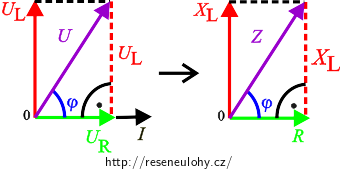
Z diagramu je vidět, že pro celkovou impedanci Z platí
\[ Z = \sqrt{R^2 + {X_\mathrm{L}}^2 } \]a odtud vyjádříme induktanci cívky XL:
\[ X_\mathrm{L} = \sqrt{ Z^2 - R^2}. \]Indukčnost cívky L vyjádříme z definice induktance XL:
\[X_\mathrm{L} = \omega L = 2 \pi f \mathrm{L}\] \[ L = \frac{X_\mathrm{L}}{2 \pi f}, \]kam ještě dosadíme vztah pro induktanci cívky XL:
\[ L = \frac{\sqrt{ Z^2 - R^2} }{2 \pi f} .\]
d) Vztah pro fázový posun φ mezi střídavým napětím a proudem cívkou získáme také pomocí výše nakresleného diagramu:
\[ \cos\,\varphi = \frac{R}{Z}= \frac{\frac{U_1}{I_1}}{\frac{U_2}{I_2}}=\frac{U_1 I_2}{U_2 I_1}. \]Zápis a číselné dosazení
U1 = 24 V stejnosměrné napětí zdroje I1 = 0,1 A proud cívkou při stejnosměrném napětí U2 = 24 V efektivní hodnota střídavého napětí zdroje I2 = 50 mA efektivní hodnota proudu tekoucí cívkou při střídavém napětí f = 50 Hz frekvence napětí zdroje
\[\mathrm{a)}\ R = \frac{U_1}{I_1}=\frac{24}{0{,}1}\,\mathrm\Omega=240\,\mathrm\Omega \] \[\mathrm{b)}\ Z = \frac{U_2}{I_2}=\frac{24}{0{,}05}\,\mathrm\Omega=480\,\mathrm\Omega \] \[\mathrm{c)}\ X_\mathrm{L} = \sqrt{Z^2 - R^2}=\sqrt{480^2-240^2}\,\mathrm\Omega\,\dot{=}\,420\,\mathrm \Omega \] \[\ \ \, \, \ L = \frac{\sqrt{ Z^2 - R^2} }{2 \pi f}= \frac{\sqrt{ 480^2 - 240^2} }{2\cdot \pi \cdot 50}\,\mathrm H = 1{,}3\,\mathrm H\] \[\mathrm{d)}\ \cos\,\varphi = \frac{U_1 I_2}{U_2 I_1}=\frac{24{\cdot} 0{,}05}{24 {\cdot} 0{,}1} =0{,}5\ \Rightarrow\ \varphi = 60^{\circ} \]Odpověď
Elektrický odpor cívky je 240 Ω. Celková impedance cívky má hodnotu 480 Ω a induktance cívky je přibližně 420 Ω v daném obvodu. Fázový posun mezi střídavým napětím a proudem cívkou v uvedeném zapojení má hodnotu přibližně 60°. Indukčnost cívky je asi 1,3 H.


