Využití Kirchhoffových zákonů pro výpočet celkového odporu zapojení
Úloha číslo: 10
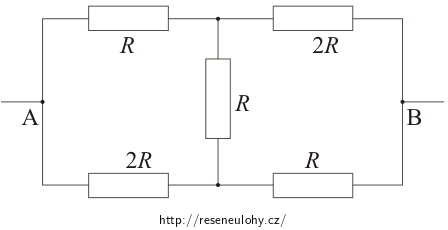
Na obrázku je nakresleno schéma zapojení 5 rezistorů. Určete odpor tohoto zapojení mezi body A a B. Hodnoty odporů jsou označeny v obrázku.
Nápověda
Vyhledejte si Kirchhoffovy zákony a zkuste je použít.
Rozbor
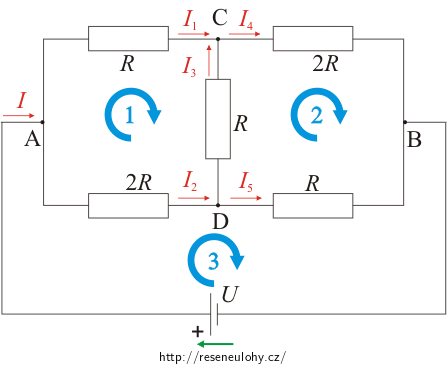
1. Představíme si, že jsme obvod v bodech A, B připojili ke zdroji napětí U (předpokládáme, že zdroj má nulový vnitřní odpor).
2. U zdroje si vyznačíme šipkou směr elektromotorického napětí.
3. V obrázku si označíme proudy a zvolíme jejich směr.
4. Zvolíme uzavřené smyčky a jejich směr.
5. Napíšeme si rovnice podle I. a II. Kirchhoffova zákona.
6. Řešíme rovnice.
Podrobnější popis použití Kirchhoffových zákonů najdete u příkladu Použití Kirchhoffových zákonů pro řešení obvodu se dvěma zdroji.
1. část řešení - sestavení rovnic
Odpor mezi body A a B vypočítáme za pomoci Ohmova zákona:
\[U\,=\, R_\mathrm{celk}I\,.\]Musíme tedy spočítat celkový proud, který by zapojením tekl, pokud bychom ho připojili ke zdroji napětí U.
Z prvního Kirchhoffova zákona získáme rovnice pro 4 uzly:
\[I\,=\, I_1 + I_2\,=\, I_4 + I_5, \tag{uzly A, B}\] \[I_1 + I_3\,=\, I_4,\tag{uzel C}\] \[I_2\,=\, I_3 + I_5.\tag{uzel D}\]Z druhého Kirchhoffova zákona dostáváme:
\[RI_1 - RI_3 - 2RI_2\,=\, 0\,\Rightarrow\,I_1-I_3-2I_2\,=\,0,\tag{smyčka 1}\] \[RI_3 + 2RI_4 - RI_5\,=\, 0\,\Rightarrow\,I_3+2I_4-I_5\,=\,0,\tag{smyčka 2}\] \[U\,=\, 2RI_2 + RI_5.\tag{smyčka 3}\]Nyní jsme dostali 6 rovnic pro 6 neznámých (I, I1, I2, I3, I4, I5).
Tím končí fyzikální část řešení. Abychom se dostali k výsledku, musíme v dalším postupu řešit uvedenou soustavu rovnic.
2. část řešení - řešení soustavy rovnic
Rovnice pro smyčku 1 a 2 sečteme a dostaneme:
\[I_1 - 2I_2 - I_5 + 2I_4\,=\,0\,.\]Proudy I1 a I5 si vyjádříme z rovnice (uzly A, B) a dosadíme do předchozí rovnice:
\[I_1\,=\, I - I_2\,,\hspace{20px}I_5\,=\, I - I_4\,,\]
takže dostáváme vztah
\[I - I_2 - 2I_2\,=\, I - I_4 - 2I_4\]a tedy rovnosti
\[I_2\,=\, I_4\hspace{20px}\mathrm{a}\hspace {20px}I_1\,=\, I_5\,.\]
Tím se nám soustava rovnic zjednoduší na:
\[I\,=\,I_1+I_2,\tag{1}\] \[I_1+I_3\,=\,I_2,\tag{2}\] \[I_1-I_3-RI_2\,=\,0,\tag{3}\] \[U\,=\,2RI_2+RI_1.\tag{4}\]Do rovnice (3) dosadíme I3 z rovnice (2):
\[ I_1 - (I_2-I_1) - 2I_2\,=\, 0, \] \[ 2I_1 - 3I_2\,=\, 0\,.\]Tím dostaneme vztah pro I1:
\[I_1\,=\, \frac{3}{2}I_2\,.\]K výpočtu celkového odporu ostatní neznámé nepotřebujeme, a proto soustavu rovnic nebudeme dále řešit.
3. část řešení - výpočet celkového odporu
Nyní se vrátíme k Ohmovu zákonu
\[U\,=\, R_\mathrm{celk}I\, =\, R_\mathrm{celk}(I_1 + I_2)\]a z něj si vyjádříme Rcelk:
\[R_\mathrm{celk}\,=\, \frac{U}{I_1+I_2}\,.\]Z druhého Kirchhoffova zákona již víme (rovnice (4) z minulého oddílu), že
\[U\,=\,2RI_2+RI_1\,,\]a v minulém oddíle jsme si spočítali, že
\[I_1\,=\,\frac{3}{2}I_2\,.\]Obojí dosadíme do vzorce pro celkový odpor
\[R_\mathrm{celk}\,=\, \frac{2RI_2+RI_1}{I_1+I_2}\,=\,\frac{2RI_2+\frac{3}{2}RI_2}{\frac{3}{2}I_2+I_2}\] \[R_\mathrm{celk}\,=\, \frac{R(2+\frac{3}{2})I_2}{(\frac{3}{2}+1)I_2}\,=\, \frac{7}{5}R\,.\]Zjednodušení
Díky tomu, že obvod je „symetrický“, není důvod, aby proudy I1 a I5 byly různé. Totéž samozřejmě platí i pro proudy I2 a I4.
Z Kirchhoffových zákonů tedy ihned dostaneme rovnice:
\[I\, =\, I_1 + I_2\tag{1.KZ, uzel A}\] \[I_1+I_3 \,=\, I_2\tag{2.KZ, uzel C}\] \[RI_1 - RI_3 - 2RI_2 \,=\, 0\tag{smyčka 2}\] \[U\,=\,2RI_2+RI_1\tag{smyčka 3}\]Tím se rovnou dostáváme do poloviny 2. části řešení.
Odpověď
Celkový odpor sítě Rcelk mezi body A, B je \(R_\mathrm{celk}\,=\, \frac{7}{5}R\).
Podobná úloha
Použití Kirchhoffových zákonů pro řešení obvodu se dvěma zdroji je jednodušší obdobou této úlohy.
Jiné metody řešení
Tuto úlohu můžeme také řešit transformací „trojúhelníku“ na „hvězdu“ (viz Transformace trojúhelník - hvězda).




