Jak vyhodit kuličku?
Úloha číslo: 780
Na stromě ve výšce 5 m nad zemí visí kulička nesoucí kladný náboj 5 µC. Jakou rychlostí musíme z bodu ležícího na povrchu Země přímo pod visící kuličkou vrhnout svisle vzhůru kuličku o hmotnosti 5 g a záporném náboji −10 µC, aby se kuličky k sobě přitáhly?
Nápověda 1
Jaké síly působí na vyhozenou kuličku? Rozmyslete si, které síly se při pohybu mění (závisí na vzdálenosti) a které zůstávají stejné (nezávisí na vzdálenosti).
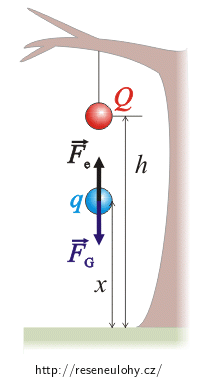
Obrázek
Nápověda 2
V úloze hledáme rychlost, kterou je třeba vyhodit kuličku, aby vystoupala do takové výšky, kde elektrická síla bude větší než tíhová. Kulička pak bude elektrickou silou přitažena nahoru, protože tíhová síla nebude dostatečně velká, aby „donutila“ kuličku spadnout dolů.
Z velikostí sil vyjádřete tuto výšku.
Nápověda 3
K hledání velikosti rychlosti je vhodné využít zákona zachování mechanické energie.
Jaké energie se v úloze vyskytují?
Nápověda 4
Práce vykonaná elektrickou silou je dána vztahem: \[W\,=\,\frac{Qq}{4\pi\varepsilon_0}\left(\frac{1}{r_1} - \frac{1}{r_2} \right).\]Tento vztah je odvozen v úloze Práce vykonaná při přenesení náboje.
Rozbor
Na vyhozenou kuličku působí tíhová síla a elektrická síla, kterou ji přitahuje kulička zavěšená na stromě. Čím blíže k sobě jsou kuličky, tím větší je elektrická síla. K přitažení obou kuliček dojde v případě, že kulička vystoupá do místa, kde je elektrická síla stejně velká jako síla tíhová.
Z porovnání velikosti sil zjistíme vzdálenost, při které se již kuličky přitáhnou.
Velikost počáteční rychlosti zjistíme ze zákona zachování energie. Součet počáteční kinetické energie kuličky a práce, kterou vykoná elektrická síla, musí být stejný jako potenciální tíhová energie kuličky v místě, ze kterého se kuličky již přitáhnou.
Řešení
Na svisle vzhůru vrženou kuličku bude působit tíhová síla \(\vec{F}_\mathrm{G}\) a elektrostatická síla \(\vec{F}_\mathrm{e}\). Zatímco tíhová síla bude vzhledem ke skutečnosti, že se pohybujeme v homogenním tíhovém poli Země, konstantní, elektrostatická síla se bude s přibližováním obou kuliček zvětšovat.
K přitažení obou kuliček dojde v případě, že vržená kulička dosáhne bodu, kdy obě uvedené síly budou mít stejnou velikost. Výšku tohoto bodu x nad zemí určíme pomocí Coulombova zákona a známého vztahu pro velikost tíhové síly.
Bude platit:
\[F_\mathrm{G}\,=\,F_\mathrm{e}\,\] \[mg\,=\, \frac{1}{4\pi\varepsilon_0}\,\frac{Q q}{\left( h-x\right)^2}\,,\]kde Q je náboj zavěšené kuličky a q je náboj vyhozené kuličky.
Vyjádříme si neznámou vzdálenost x:
\[\left( h-x\right)^2 \,=\, \frac{1}{4\pi\varepsilon_0}\,\frac{Q q}{mg}\] \[h-x \,=\,\sqrt{ \frac{1}{4\pi\varepsilon_0}\,\frac{Q q}{mg}}\] \[x \,=\,h \,-\, \sqrt{ \frac{1}{4\pi\varepsilon_0}\,\frac{Q q}{mg}}\] \[x \,=\,h \,-\, \sqrt{\frac{Q q}{4\pi\varepsilon_0mg}}.\]K tomu, abychom určili minimální počáteční rychlost, při níž dojde ke spojení kuliček, zapojíme do hry zákon zachování energie. Budeme uvažovat mezní případ, kdy kulička dosáhne požadovaného bodu v okamžiku, kdy je její rychlost nulová.
Součet počáteční kinetické energie a práce, kterou vykonala elektrostatická síla, se musí rovnat potenciální tíhové energii v uvažovaném bodě:
\[E_\mathrm{k} \,+\,W\,=\,E_\mathrm{p}.\]Uvědomíme-li si, že práce vykonaná elektrostatickou silou při přiblížení bodového náboje q k dalšímu bodovému náboji Q, který je opačné polarity, ze vzdálenosti r1 na vzdálenost r2 je dána vztahem
\[W\,=\,\frac{Qq}{4\pi\varepsilon_0}\left( \frac{1}{r_1} - \frac{1}{r_2} \right)\,,\]můžeme předchozí vztah upravit:
\[\frac{1}{2}mv^2 \,+\,\frac{Qq}{4\pi\varepsilon_0}\left( \frac{1}{h-x} - \frac{1}{h} \right)\,=\,mgx\] \[\frac{1}{2}mv^2 \,=\,mgx\,-\,\frac{Qq}{4\pi\varepsilon_0}\left( \frac{1}{h-x} - \frac{1}{h} \right).\]Vztah budeme upravovat tak, abychom vyjádřili neznámou v:
\[v^2 \,=\,2gx\,-\,\frac{Qq}{2\pi\varepsilon_0 m}\left( \frac{1}{h-x} - \frac{1}{h} \right)\] \[v \,=\,\sqrt{2gx\,-\,\frac{Qq}{2\pi\varepsilon_0 m}\left( \frac{1}{h-x} - \frac{1}{h} \right)}.\]Dosadíme vztah pro vzdálenost x a vztah zjednodušíme:
\[v=\sqrt{2g \left(h \,-\, \sqrt{\frac{Q q}{4\pi\varepsilon_0mg}}\right)\,-\,\frac{Qq}{2\pi\varepsilon_0 m}\left( \frac{1}{h-\left(h \,-\, \sqrt{\frac{Q q}{4\pi\varepsilon_0mg}} \right)} - \frac{1}{h} \right)}\] \[v=\sqrt{2g \left(h \,-\, \sqrt{\frac{Q q}{4\pi\varepsilon_0mg}}\right)\,-\,\frac{Qq}{2\pi\varepsilon_0 m}\left( \frac{1}{ \sqrt{\frac{Q q}{4\pi\varepsilon_0mg}} } - \frac{1}{h} \right)}\] \[v=\sqrt{2g \left(h \,-\, \sqrt{\frac{Q q}{4\pi\varepsilon_0mg}}\right)\,-\,\frac{Qq}{2\pi\varepsilon_0 m}\left( \sqrt{\frac{4\pi\varepsilon_0mg}{Q q} } - \frac{1}{h} \right)}.\]Zápis a číselný výpočet
h = 5 m
Q = 5 µC = 5·10−6 C
m = 5 g = 5·10−3 kg
q = 10 µC = 10·10−6 C = 10−5 C
v = ? (m·s−1)
\[v=\sqrt{2g \left(h \,-\, \sqrt{\frac{Q q}{4\pi\varepsilon_0mg}}\right)\,-\,\frac{Qq}{2\pi\varepsilon_0 m}\left( \sqrt{\frac{4\pi\varepsilon_0mg}{Q q} } - \frac{1}{h} \right)}\] \[v = \sqrt{ 2{\cdot} 9{,}81\cdot \left(5 \,-\, \sqrt{\frac{5{\cdot} 10^{-6}\cdot 10^{-5} }{4\pi\cdot\,8{,}85 {\cdot} 10^{-12}\cdot5 {\cdot} 10^{-3} \cdot 9{,}81}}\right)\,- \\ -\,\frac{5{\cdot} 10^{-6}\cdot 10^{-5} }{2\pi\cdot\,8{,}85 {\cdot} 10^{-12}\cdot 5{\cdot} 10^{-3} }\cdot\left( \sqrt{\frac{4\pi\cdot\,8{,}85 {\cdot} 10^{-12}\cdot 5{\cdot}10^{-3} \cdot 9{,}81}{5{\cdot} 10^{-6}\cdot 10^{-5} }} - \frac{1}{5} \right)}\] \[v\dot{=}\,3{,}9\,\mathrm{m·s}^{-1}\]Výpočet můžeme provést také postupným dosazováním. Vyhneme se tím dlouhému výrazu pod odmocninou.
\[\begin{eqnarray} x \,&=&\,h \,-\, \sqrt{\frac{Q q}{4\pi\varepsilon_0mg}} \,=\,5 \,-\, \sqrt{\frac{5{\cdot} 10^{-6}\cdot 10^{-5} }{4\pi\cdot\,8{,}85 {\cdot} 10^{-12}\cdot5 {\cdot} 10^{-3} \cdot 9{,}81}}\\ x \,&\dot=&\,2\,\mathrm{m}\\ \\ W\,&=&\, \frac{Qq}{4\pi\varepsilon_0}\left( \frac{1}{h-x} - \frac{1}{h} \right)\,\mathrm{J} \,=\, \frac{5{\cdot} 10^{-6}\cdot 10^{-5}}{4\pi\cdot\,8{,}85 {\cdot} 10^{-12}}\left( \frac{1}{5-2} - \frac{1}{5} \right)\,\mathrm{J} \,\dot=\,0{,}06\,\mathrm{J} \\ \\ E_\mathrm{p}\,&=&\,mgx\,=\,5{\cdot} 10^{-3}\cdot 9{,}81 {\cdot} 2\,\dot=\,0{,}1\,\mathrm{J}\\ \\ E_\mathrm{k}\,&=&\,E_\mathrm{p}-W\,=\,0{,}1\,\mathrm{J}-0{,}06\,\mathrm{J}\,\dot=\,0{,}04\,\mathrm{J}\\ \\ v\,&=&\,\sqrt{\frac{2E_\mathrm{k}}{m}}\,=\,\sqrt{\frac{2{\cdot} 0{,}04}{5{\cdot}10^{-3}}}\,\mathrm{m·s^{-1}}\\ v\,&\dot=&\,4\,\mathrm{m·s^{-1}} \end{eqnarray}\]Odpověď
Aby se kuličky přitáhly k sobě, musíme kuličku vyhodit rychlostí přibližně 3,9 m·s−1.