Úhlová frekvence sériového RLC obvodu
Úloha číslo: 772
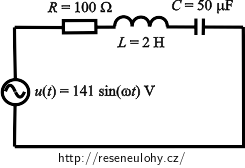
Při jaké úhlové frekvenci ω protéká větví obvodu podle obrázku proud o efektivní hodnotě 1 A?
Nápověda – okamžitý průběh napětí
Vyhledejte si rovnice, kterými popisujeme okamžité hodnoty střídavého napětí a proudu.
Nápověda – impedance sériového RLC obvodu
Známe napětí a proud v obvodu. Co musí platit pro jeho impedanci?
Odvoďte si nebo vyhledejte vztah pro výpočet celkové impedance sériového RLC obvodu.
Rozbor
Hledanou úhlovou frekvenci sériového RLC obvodu vyjádříme z Ohmova zákona pro obvod se střídavým napětím. Efektivní hodnotu napětí určíme z rovnice pro okamžitý průběh napětí v obvodu.
Řešení
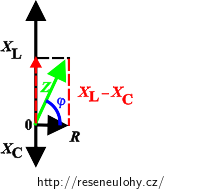
Velikost úhlové frekvence ω odvodíme z celkové impedance sériového RLC obvodu Z, kterou vyjádříme pomocí induktance cívky XL, kapacitance kondenzátoru XL a odporu rezistoru R:
\[Z = \sqrt{R^2+(X_\mathrm{L}-X_\mathrm{C})^2} .\]Dosadíme za induktanci cívky XL a kapacitanci kondenzátoru XC, abychom do výrazu dostali úhlovou frekvenci ω :
\[ Z = \sqrt{R^2+(\omega L- \frac{1}{\omega C})^2}. \]Vyjádříme úhlovou frekvenci ω:
\[Z^2 = R^2+(\omega L- \frac{1}{\omega C})^2 ,\] \[ Z^2-R^2= (\omega L- \frac{1}{\omega C})^2 ,\] \[ \sqrt{Z^2-R^2} = \omega L- \frac{1}{\omega C} ,\] \[ \omega C \sqrt{Z^2-R^2}= {\omega}^2 LC - 1. \]Získali jsme kvadratickou rovnici pro neznámou úhlovou frekvenci ω:
\[ {\omega}^2 LC - \omega C \sqrt{Z^2-R^2} - 1 = 0,\]kterou řešíme pomocí diskriminantu:
\[ \mathrm{D} = C^2(Z^2-R^2) + 4LC. \]Úhlová frekvence nabývá ω hodnot:
\[ \omega_{1{,}2} = \frac{ C \sqrt{Z^2-R^2} \pm \sqrt{C^2(Z^2-R^2) + 4LC}}{2LC}. \]
Velikost celkové impedance obvodu Z odvodíme pomocí Ohmova zákona pro obvod se střídavým proudem:
\[ Z = \frac{U}{I},\]kde U je efektivní hodnota napětí a I efektivní hodnota proudu.
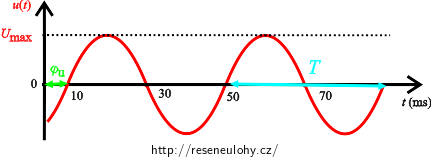
Efektivní hodnotu napětí U vypočteme z rovnice pro okamžitou hodnotu napětí u(t). Tato rovnice má obecný tvar:
\[ u(t) = U_\mathrm{max} \, \sin(\omega t + {\varphi}_0), \]kde Umax je maximální hodnota napětí a φ0 je fázové posunutí mezi napětím a proudem.
Ze zadání víme, že
\[ u(t) = 141\, \sin(\omega t)\,\mathrm{V}, \]odkud vyjádříme maximální Umax a poté i efektivní hodnotu napětí U:
\[ U = \frac{U_\mathrm{max}}{\sqrt 2} . \]
Dosadíme za celkovou impedanci Z do výrazu pro výpočet úhlové frekvence ω:
\[ \omega_{1{,}2} = \frac{ C \sqrt{\left(\frac{U}{I}\right)^2-R^2} \pm \sqrt{C^2\left(\left(\frac{U}{I}\right)^2-R^2\right)+ 4LC}}{2LC}. \]Zápis a číselné dosazení
R = 100 Ω odpor rezistoru L = 2 H indukčnost cívky C = 50 μF = 50·10-6 F kapacita kondenzátoru I = 1 A efektivní hodnota proudu u(t) = 141 sin(ωt) V časový průběh okamžité hodnoty napětí ω = ? (s-1) úhlová frekvence
\[ U = \frac{U_\mathrm{max}}{\sqrt 2} = \frac{141}{\sqrt 2} \,\mathrm{V}\dot=100\,\mathrm V. \]
\[ {\omega}_1 = \frac{ C \sqrt{\left(\frac{U}{I}\right)^2-R^2} + \sqrt{C^2\left(\left(\frac{U}{I}\right)^2-R^2\right) + 4LC}}{2LC} \,\dot= \] \[\dot=\,\frac{ 50 {\cdot} 10^{-6}{\cdot}\sqrt{(\frac{100}{1})^2-100^2} + \sqrt{ 50 {\cdot} 10^{-6} {\cdot}\left((\frac{100}{1})^2-100^2\right) + 4{\cdot} 2 {\cdot} 50 {\cdot} 10^{-6} }}{2{\cdot} 2 \cdot 50 {\cdot} 10^{-6}} \,\mathrm{s^{-1}}\ \dot=100\,\mathrm{s^{-1}}.\] \[ {\omega}_2 = \frac{ C \sqrt{\left(\frac{U}{I}\right)^2-R^2} - \sqrt{\left(\frac{U}{I}\right)^2-R^2 + 4LC}}{2LC}\,\dot=\] \[\dot=\frac{ 50 {\cdot} 10^{-6} {\cdot} \sqrt{(\frac{100}{1})^2{-}100^2} {-} \sqrt{ 50 {\cdot} 10^{-6} {\cdot}\left( (\frac{100}{1})^2-100^2\right) + 4{\cdot} 2 {\cdot} 50 {\cdot} 10^{-6} }}{2{\cdot} 2 \cdot 50 {\cdot} 10^{-6}}\,\mathrm{s^{-1}}\,\dot=\,-100\,\mathrm{s^{-1}}.\]Pozn.: Fyzikální význam má pouze hodnota úhlové frekvence ω1, protože hodnota úhlové frekvence ω2 vyšla po dosazení zadaných hodnot záporně.
Odpověď
Aby obvodem protékal proud o efektivní hodnotě 1 A, musí být velikost úhlové frekvence asi 100 s-1.
Komentář – řešení pomocí triku
Zadané hodnoty napětí, proudu a odpor rezistoru vyhovují Ohmovu zákonu:
\[\frac{U_\mathrm{ef}}{I_\mathrm{ef}} = R \qquad\Rightarrow\qquad\frac{100\,\mathrm{V}}{1\,\mathrm{A}}=100\,\mathrm{\Omega}.\tag{*}\]Při zadaném proudu se obvod tedy chová, jako kdyby v něm byl zapojen pouze rezistor. Vliv cívky a kondenzátoru se navzájem ruší, to znamená, že daný obvod je v rezonanci. Pokud je obvod v rezonanci, lze úhlovou frekvenci odvodit přímo z Thomsonova vztahu:
\[ \omega = \frac{1} {\sqrt {LC}} = \frac{1}{\sqrt{2 {\cdot} 50 \cdot 10^{-6}}} \,\mathrm {Hz}=100\,\mathrm {Hz}. \]Ještě můžeme zkusit, zda se nám za předpokladu (*) podaří upravit obecné řešení na Thomsonův vztah. Připoměňme obecné řešení:
\[ \omega = \frac{ C \sqrt{\left(\frac{U_\mathrm{ef}}{I_\mathrm{ef}}\right)^2-R^2} + \sqrt{\left(\frac{U_\mathrm{ef}}{I_\mathrm{ef}}\right)^2-R^2 + 4LC}}{2LC}. \]Z předpokladu (*) plyne
\[\frac{U_\mathrm{ef}}{I_\mathrm{ef}} = R \qquad\Rightarrow\qquad(\frac{U_\mathrm{ef}}{I_\mathrm{ef}})^2-R^2=0.\]Pro úhlovou frekvenci ω lze tedy psát:
\[ \omega = \frac{ C \sqrt{0} + \sqrt{0 + 4LC}}{2LC}= \frac{ \sqrt{ 4LC}}{2LC}= \frac{1} {\sqrt {LC}}. \]