Průběh napětí a proudu na spotřebiči
Úloha číslo: 514
Na následujících grafech je znázorněn průběh napětí na spotřebiči a proudu tímto spotřebičem.
1)
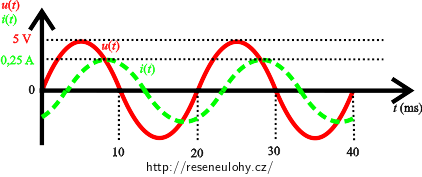
2)
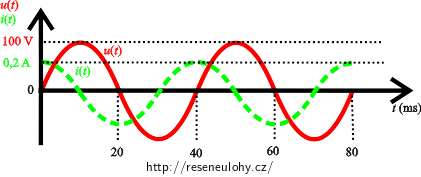
3)
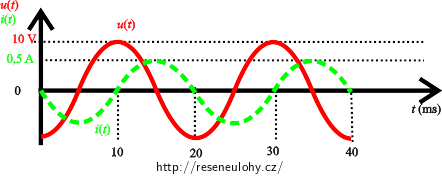
Pro všechny případy určete:
a) frekvenci zdroje,
b) maximální hodnotu a efektivní hodnotu napětí a proudu,
c) jak velký je fázový posun mezi napětím a proudem a zda u spotřebiče převládá induktance nebo kapacitance.
d) Napište vztahy pro okamžitou hodnotu proudu a napětí.
Nápověda – efektivní hodnota
Definice: Efektivní hodnota střídavého napětí odpovídá hodnotě stejnosměrného napětí, které v daném obvodu vykoná za stejný čas (mnoho period) stejnou práci jako napětí střídavé (podrobněji viz úloha Výkon střídavého proudu v rezistoru).
Najděte si vztah mezi maximální a efektivní hodnotou střídavého harmonického napětí.
Nápověda – kapacitní a indukční charakter
Má-li spotřebič indukční charakter, znamená to, že induktance daného spotřebiče je větší v porovnání s jeho kapacitancí. Převládá-li induktance, napětí na spotřebiči předbíhá proud.
Analogicky: Má-li spotřebič kapacitní charakter, znamená to, že kapacitance daného spotřebiče je větší v porovnání s jeho induktancí. Převládá-li kapacitance, napětí na spotřebiči se zpožďuje za proudem.
Nápověda – průběh střídavého napětí a proudu
Průběh střídavého napětí popisujeme obecně pomocí rovnice:
\[ u(t) = U_\mathrm{max}\, \sin( 2 \pi f t + \varphi_\mathrm{u} ), \]kde Umax je maximální hodnota amplitudy napětí, f frekvence napětí zdroje a φu je počáteční fáze napětí.
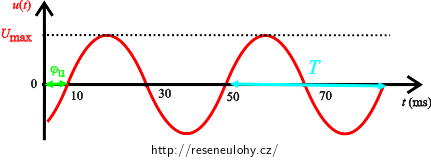
Rovnici pro průběh proudu určíme stejně.
Pozn.: Počáteční fáze proudu φi či napětí φu neodpovídá fázovému posunu φ mezi proudem a napětím. Mezi těmito veličinami platí vztah:
\[ {\varphi}= {\varphi}_\mathrm{u} - {\varphi}_\mathrm{i}. \]Řešení grafu č. 1
a) Frekvence napětí zdroje
Frekvenci f určíme jako převrácenou hodnotu periody T, která udává dobu trvání jednoho opakování periodického děje.
.page.tagged.png "Průběh napětí a proudu")
Z grafu je zřejmé, že perioda T je rovna 20 ms, protože za tuto dobu dosáhne napětí všech možných hodnot.
Tedy platí:
\[ f= \frac{1}{T}. \]Dosadíme číselně:
\[ f= \frac{1}{T} = \frac{1}{0{,}02}\,\mathrm Hz= 50\,\mathrm Hz . \]
b) Maximální a efektivní hodnota napětí a proudu zdroje
Maximální hodnotu napětí i proudu odečteme přímo z grafu:
\[ U_\mathrm{max}=5\,\mathrm V,\] \[ I_\mathrm{max}=0{,}25\,\mathrm A.\].page.tagged.png "Průběh napětí a proudu")
Mezi maximální a efektivní hodnotou střídavého napětí (resp. proudu) platí vztah:
\[ U_\mathrm{ef} = \frac{U_\mathrm{max}}{\sqrt 2}, \] \[ I_\mathrm{ef} = \frac{I_\mathrm{max}}{\sqrt 2}. \]Dosadíme číselně:
\[ U_\mathrm{ef} = \frac{U_\mathrm{max}}{\sqrt 2}=\frac{5}{\sqrt 2}\,\mathrm V \dot=3{,}5 \,\mathrm V , \] \[ I_\mathrm{ef} = \frac{I_\mathrm{max}}{\sqrt 2}=\frac{0{,}25}{\sqrt 2}\,\mathrm A \dot=0{,}18 \,\mathrm A . \]
c) Kapacitní a indukční charakter a fázový posun mezi napětím a proudem
Zda má střídavý obvod kapacitní nebo indukční charakter poznáme z grafu podle toho, zda napětí předbíhá proud nebo se naopak za proudem zpožďuje.
.page.tagged.png "Fázový posun mezi napětím a proudem")
V tomto případě jako první dosáhne svého maxima napětí v čase 5 ms (proud dosáhne maxima až v čase kolem 8 až 9 ms). Takže napětí předbíhá proud → tento obvod má indukční charakter.
Fázové posunutí φ napětí vůči proudu tedy bude kladné. Z grafu je vidět, že fázový posun je zcela určitě v intervalu (0, π/2) a můžeme odhadnout, že jeho hodnota je přibližně π/3.
d) Vztahy pro okamžitou hodnotu proudu a napětí
Pro okamžitou hodnotu napětí platí
\[ u(t) = U_\mathrm{max}\, \sin(2 \pi f t + \varphi_u ) \]a pro okamžitou hodnotu proudu platí
\[ i(t) = I_\mathrm{max}\, \sin(2 \pi f t + \varphi_i). \]Počáteční fázi napětí i proudu určíme z grafu:
\[\varphi_\mathrm{u} = 0\] \[\varphi_\mathrm{i} \dot{=} -\frac{\pi}{3}. \]Dosadíme číselné hodnoty do obecných vyjádření:
\[ u(t) =5\cdot \sin(2\cdot \pi \cdot 50 \cdot t )\,\mathrm V =5\cdot \sin(100\cdot \pi \cdot t )\,\mathrm V, \] \[ i(t) \dot= 0{,}25 \cdot \sin(2\cdot \pi \cdot 50 \cdot t - \frac{\pi}{3})\,\mathrm A = 0{,}25 \cdot \sin(100\cdot \pi \cdot t - \frac{\pi}{3})\,\mathrm A. \]Pro úplnost si ověříme vztah mezi počátečními fázemi napětí a proudu a fázovým posunutím:
\[\varphi = {\varphi}_\mathrm{u} - {\varphi}_\mathrm{i} = 0- (- \frac{\pi}{3}) = \frac{\pi}{3} .\]Řešení grafu č.2
a) Frekvence napětí zdroje
.page.tagged.png "Průběh napětí a proudu")
Z grafu je zřejmé, že perioda T je rovna 40 ms a tedy platí:
\[ f= \frac{1}{T} = \frac{1}{0{,}04}\,\mathrm Hz= 25\,\mathrm Hz . \]
b) Maximální a efektivní hodnota napětí a proudu zdroje
Maximální hodnotu napětí i proudu odečteme rovnou z grafu:
\[ U_\mathrm{max}=100\,\mathrm V,\] \[ I_\mathrm{max}=0{,}2\,\mathrm A\].page.tagged.png "Průběh napětí a proudu")
a dosadíme do vztahů mezi maximální a efektivní hodnotou střídavého napětí (resp. proudu):
\[ U_\mathrm{ef} = \frac{U_\mathrm{max}}{\sqrt 2}=\frac{100}{\sqrt 2}\,\mathrm V \dot=71 \,\mathrm V , \] \[ I_\mathrm{ef} = \frac{I_\mathrm{max}}{\sqrt 2}=\frac{0{,}2}{\sqrt 2}\,\mathrm A \dot=0{,}14 \,\mathrm A . \]
c) Kapacitní a indukční charakter a fázový posun mezi napětím a proudem
.page.tagged.png "Průběh napětí a proudu")
V tomto případě jako první dosáhne svého maxima proud. Takže napětí se zpožďuje za proudem a tento obvod má kapacitní charakter.
Z grafu je vidět, že fázový posun φ mezi napětím a proudem bude přibližně − π/2.
d) Vztahy pro okamžitou hodnotu proudu a napětí
Pro okamžitou hodnotu napětí platí
\[ u(t) = U_\mathrm{max}\, \sin(2 \pi f t + \varphi_\mathrm{u}) \]a pro okamžitou hodnotu proudu:
\[ i(t) = I_\mathrm{max}\, \sin(2 \pi f t + \varphi_\mathrm{i}). \]Počáteční fázi napětí i proudu určíme z grafu:
\[\varphi_\mathrm{u} = 0,\] \[\varphi_\mathrm{i} = \frac{\pi}{2}. \]Dosadíme číselné hodnoty, které jsme získali výše:
\[ u(t) =100\cdot \sin(2\cdot \pi \cdot 25 \cdot t)\,\mathrm V =100\cdot \sin(50\cdot \pi \cdot t)\,\mathrm V, \] \[ i(t) = 0{,}2 \cdot \sin(2\cdot \pi \cdot 25 \cdot t + \frac{\pi}{2})\,\mathrm A = 0{,}2 \cdot \sin(50\cdot \pi \cdot t + \frac{\pi}{2})\,\mathrm A. \]Pro úplnost ověříme vztah počátečními fázemi napětí a proudu a fázovým posunutím:
\[\varphi = {\varphi}_\mathrm{u} - {\varphi}_\mathrm{i} = 0- \frac{\pi}{2} =- \frac{\pi}{2} .\]Řešení grafu č.3
a) Frekvence napětí zdroje
.page.tagged.png "Průběh napětí a proudu")
Z grafu je zřejmé, že perioda T je rovna 20 ms a tedy platí:
\[ f= \frac{1}{T} = \frac{1}{0{,}02}\,\mathrm Hz= 50\,\mathrm Hz . \]
b) Maximální a efektivní hodnota napětí a proudu zdroje
\[ U_\mathrm{max}=10\,\mathrm V,\] \[ I_\mathrm{max}=0{,}5\,\mathrm A.\].page.tagged.png "Průběh napětí a proudu")
Po dosazení do vztahů mezi maximální a efektivní hodnotou střídavého napětí (resp. proudu) dostáváme:
\[ U_\mathrm{ef} = \frac{U_\mathrm{max}}{\sqrt 2}=\frac{10}{\sqrt 2}\,\mathrm V \dot=7{,}1 \,\mathrm V , \] \[ I_\mathrm{ef} = \frac{I_\mathrm{max}}{\sqrt 2}=\frac{0{,}5}{\sqrt 2}\,\mathrm A \dot=0{,}36 \,\mathrm A . \]
c) Kapacitní a indukční charakter a fázový posun mezi napětím a proudem
.page.tagged.png "Průběh napětí a proudu")
V tomto případě jako první dosáhne svého maxima napětí. Takže napětí předbíhá proud a tento obvod má indukční charakter.
Z grafu je vidět, že fázový posun φ mezi napětím a proudem bude přibližně π/2.
d) Vztahy pro okamžitou hodnotu proudu a napětí
Pro okamžitou hodnotu napětí platí
\[ u(t) = U_\mathrm{max}\, \sin(2 \pi f t + \varphi_\mathrm{u}) \]a pro okamžitou hodnotu proudu platí
\[ i(t) = I_\mathrm{max}\, \sin(2 \pi f t + \varphi_\mathrm{i}). \]Počáteční fázi napětí i proudu určíme z grafu:
\[\varphi_\mathrm{u} \cdot= - \frac{\pi}{2}\] \[\varphi_\mathrm{i} = -\pi . \]Dosadíme číselné hodnoty, které jsme získali výše:
\[ u(t) \dot= 10\cdot \sin(2\cdot \pi \cdot 50 \cdot t - \frac{\pi}{2})\,\mathrm V= 10\cdot \sin(100\cdot \pi \cdot t - \frac{\pi}{2})\,\mathrm V, \] \[ i(t) = 0{,}5 \cdot \sin(2\cdot \pi \cdot 50 \cdot t -\pi )\,\mathrm A.= 0{,}5 \cdot \sin(100\cdot \pi \cdot t -\pi )\,\mathrm A. \]Pro úplnost si ověříme vztah mezi počátečními fázemi napětí a proudu a fázovým posunutím:
\[\varphi = {\varphi}_\mathrm{u} - {\varphi}_\mathrm{i} = -\frac{\pi}{2} - (-\pi) = \frac{\pi}{2} .\]Odpověď
Výsledky úlohy jsou pro přehlednost seřazeny v následujících tabulkách:
graf č.1 graf č.2 graf č.3 frekvence f 50 Hz 25 Hz 50 Hz maximální hodnota napětí Umax 5 V 100 V 10 V maximální hodnota proudu Imax 0,25 A 0,2 A 0,5 A maximální hodnota napětí Uef 3,5 V 71 V 7,1 V maximální hodnota proudu Ief 0,18 A 0,14 A 0,36 A fázové posunutí mezi napětím a proudem φ π/3 − π/2 π/2 charakter obvodu indukční kapacitní indukční Tabulka pro rovnice okamžitého průběhu napětí:
okamžitý průběh napětí u(t), okamžitý průběh proudu i(t) graf č.1 \[ u(t) =5\cdot \sin(100\cdot \pi \cdot t )\,\mathrm V \] \[ i(t) \,\dot=\, 0{,}25 \cdot \sin(100\cdot \pi \cdot t - \frac{\pi}{3})\,\mathrm A \] graf č.2 \[ u(t) =100\cdot \sin(50\cdot \pi \ \cdot t)\,\mathrm V \] \[ i(t) \,\dot=\, 0{,}2 \cdot \sin(50\cdot \pi \cdot t + \frac{\pi}{2})\,\mathrm A \] graf č.3 \[ u(t) \,\dot=\, 10\cdot \sin(100\cdot \pi \cdot t - \frac{\pi}{2})\,\mathrm V, \] \[ i(t) = 0{,}5 \cdot \sin(100\cdot \pi \cdot t -\pi )\,\mathrm A. \]
