Magnetické pole přímého vodiče
Úloha číslo: 2133
Nápověda
Protože se jedná o homogenní rozložení proudu, bude vytvořené magnetické pole válcově symetrické. Pro určení magnetického pole použijeme Ampérův zákon.
Ampérův zákon
Celkový proud procházející plochou, kterou ohraničuje uzavřená křivka, vynásobený permeabilitou vakua se rovná integrálu magnetické indukce podél této křivky:
\[\mu_\mathrm{0} I_\mathrm{c} = \oint_\Gamma{\vec{B}}\cdot\vec{\textrm{d}l}.\]Nápověda – jak správně volit Ampérovu křivku
Při řešení úloh Ampérovým zákonem využíváme symetrie situace. Tedy použijeme takovou křivku, podél níž je magnetická indukce konstantní, popřípadě volíme takovou křivku, podél níž jsme schopni popsat průběh magnetické indukce.
V tomto případě budeme jako Ampérovu křivku volit kružnici.
Řešení – dlouhý přímý vodič
Pro určení směru magnetické indukce si vzpomeňme na Ampérovo pravidlo pravé ruky: „Jestliže palec pravé ruky ukazuje směr elektrického proudu ve vodiči, pak pokrčené prsty ukazují orientaci magnetických indukčních čar.“ Velikost magnetické indukce bude pravděpodobně záviset na procházejícímu proudu ve vodiči I a na vzdálenosti bodu od vodiče.
Úlohu máme řešit pomocí Ampérova zákona:
\[\mu_\mathrm{0} I_\mathrm{c} = \oint_\Gamma {\vec{B}}\cdot\vec{\textrm{d}l}.\]Ampérovou křivkou bude kružnice o poloměru r. Kružnice je vhodná volba Ampérovy křivky, jelikož směr vektoru magnetické indukce \(\vec{B}\) je k ní tečný, má tedy stejný směr jako infinitezimální posunutí ve směru křivky \(\vec{\textrm{d}l}.\) Ampérův zákon proto můžeme přepsat do skalárního tvaru
\[\mu_0 I_\mathrm{c} = \oint_\Gamma {{B}}\ {\textrm{d}l}.\]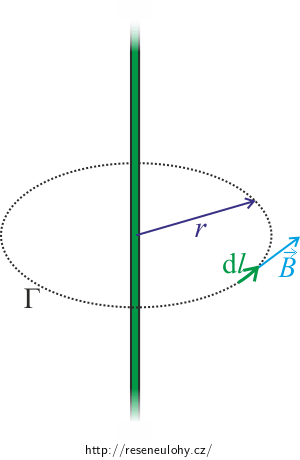
Díky symetrii také víme, že velikost magnetické indukce B je podél celé kružnice konstantní. Můžeme tedy psát
\[\oint_\Gamma {{B}}\ {\textrm{d}l}=B\oint_\Gamma \textrm{d}l,\]kde křivkový integrál přes uzavřenou křivku \(\Gamma\) je délka této křivky. Délka kružnice o poloměru r je \(2\pi r.\) \(I_\mathrm{c} \) je celkový proud procházející křivkou, tedy \(I_\mathrm{c} = I,\) což nám dohromady dává
\[\mu_0 I = B\ 2 \pi r,\]z čehož vyjádříme B:
\[B= \frac {\mu}{2\pi}\frac{I}{r}.\]Získaný výsledek nám říká, jaká je velikost magnetické indukce ve vzdálenosti r od vodiče. Směr orientace vektoru magnetické indukce můžeme určit pomocí Ampérova pravidla pravé ruky.
Nápověda – vodič o poloměru R
Jak se bude lišit výpočet magnetické indukce u vodiče o poloměru R od výpočtu s dlouhým přímým vodičem v předchozí části úlohy?
Řešení – vodič o poloměru R
Pro případ vodiče o poloměru R musíme uvažovat dva případy: magnetické pole vně vodiče a magnetické pole uvnitř vodiče.
a) vně vodiče
Výpočet magnetické intenzity vně vodiče bude stejný jako v případě přímého dlouhého vodiče a dostaneme také stejný vztah
\[B=\frac{\mu}{2\pi}\frac{I}{r},\]tento vztah platí pro \(r>R\).
b) uvnitř vodiče
Výpočet magnetického pole uvnitř vodiče bude analogický s výpočtem magnetického pole v okolí dlouhého přímého vodiče. Úlohu máme řešit pomocí Ampérova zákona:
\[\mu_0 I_\mathrm{c} = \oint_\Gamma {\vec{B}}\cdot\vec{\textrm{d}l}.\]Jako Ampérovu křivku budeme volit kružnici o poloměru r (\( R > r \)). Stejně jako vně kružnice je směr vektoru magnetické indukce \(\vec{B}\) tečný ke křivce, má tedy stejný směr jako infinitezimální posunutí ve směru křivky \(\vec{\textrm{d}l}.\) Ampérův zákon proto můžeme přepsat opět do skalárního tvaru
\[\mu_0 I_\mathrm{c} = \oint_\Gamma {{B}}\ {\textrm{d}l}.\]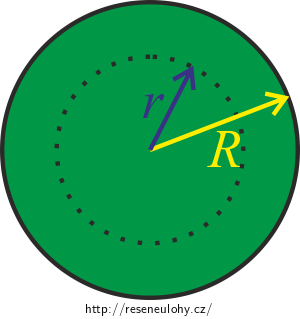
Díky symetrii také víme, že velikost magnetické indukce B je podél celé kružnice konstantní, můžeme tedy B vytknout před integrál:
\[\mu_0 I_\mathrm{c} =\oint_\Gamma {{B}}\ {\textrm{d}l}=B\oint_\Gamma \textrm{d}l = B2\pi r.\]Určitý integrál přes uzavřenou křivku \(\Gamma\) se rovná její délce, tedy délce kružnice o poloměru r (obvod kružnice je \(2\pi r\)).
\(I_\mathrm{c} \) je celkový proud procházející plochou vymezenou Ampérovou křivkou, který si vyjádříme pomocí proudové hustoty. Proudová hustota je obecně definována jako
\[j=\frac {I}{S},\]kde I je proud procházející plochou o obsahu S. Jelikož známe proud procházející vodičem, můžeme vyjádřit proudovou hustotu jako
\[j=\frac{I}{\pi R^2}.\]Když známe proudovou hustotu, můžeme vyjádřit celkový proud procházející plochou, která je vymezena Ampérovou křivkou o poloměru r (plocha je \(\pi r^2\)):
\[I_\mathrm{c} = j S = \frac{I}{\pi R^2}\pi r^2=\frac{I r^2}{R^2}.\]Vrátíme-li se zpět k našemu integrálu a dosadíme-li za celkový proud procházející plochou vymezenou Ampérovou křivkou, dostaneme
\[\mu_0 \frac{Ir^2}{ R^2} = B\ 2 \pi r,\]z čehož vyjádříme B
\[B= \frac {\mu}{2\pi}\frac{rI}{R^2}=\frac{\mu}{2\pi}\frac{I r^2}{R^2}\frac{1}{r}=\frac{\mu}{2\pi}\frac{I_c}{r}.\]Tento vztah platí uvnitř vodiče, tedy pro \( R>r.\)
Nápověda – vodič jako tlustostěnná trubka
Pokud je vodičem tlustostěnná trubka, tak je třeba si ho rozdělit na tři různé případy – oblasti. Řešení je už velmi podobné tomu, co jsme spočítali v předchozích částech úlohy.
Řešení nápovědy – vodič jako tlustostěnná trubka
Příklad budeme řešit pro
a) \(r>R_2>R_1,\)
b) \(R_2>r>R_1,\)
c) \(R_2>R_1>r.\)
Řešení – vodič jako tlustostěnná trubka
a) vně tlustostěnné trubky \((r>R_2>R_1)\)
Výpočet této části bude úplně stejný jako výpočet magnetického pole v okolí dlouhého přímého vodiče a výpočet magnetického pole v okolí vodiče o poloměru R.
Ampérovou křivkou bude kružnice o poloměru \(r>R_2>R_1\). Směr vektoru magnetické indukce \(\vec{B}\) je tečný ke křivce, má tedy stejný směr jako infinitezimální posunutí ve směru křivky \(\vec{\textrm{d}l}.\) Ampérův zákon proto můžeme přepsat do tvaru
\[\mu_0 I_\mathrm{c} = \oint_\Gamma {{B}}\ {\textrm{d}l}.\]Díky symetrii také víme, že velikost magnetické indukce B je podél celé kružnice konstantní. Můžeme tedy psát
\[\oint_\Gamma {{B}}\ {\textrm{d}l}=B\oint_\Gamma \textrm{d}l,\]kde křivkový integrál přes uzavřenou křivku \(\Gamma\) je délka této křivky, tj. \(2\pi r,\) \(I_\mathrm{c} \) je celkový proud procházející křivkou, tedy \(I_\mathrm{c} = I.\) Což nám dohromady dává
\[\mu_0 I = B\ 2 \pi r,\]z čehož vyjádříme B:
\[B= \frac {\mu}{2\pi}\frac{I}{r}.\]b) uvnitř tlustostěnné trubky \((R_2>r>R_1)\)
Tato úloha je řešena zde Dutý válcový vodič, Řešení a).
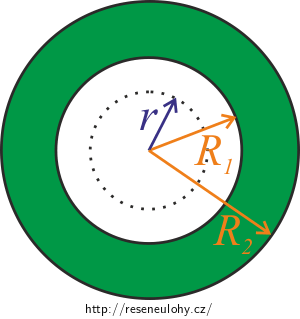
c) uvnitř tlustostěnné trubky \((R_2>R_1>r)\)
Výpočet je téměř stejný jako pro případ vně tlustostěnné trubky. Rozdílné je, že Ampérovou křivkou je kružnice o poloměru \(R_2>R_1>r\). Dále je rozdílné, že proud procházející uzavřenou Ampérovou křivkou je nulový, tedy \(I=0\ \mathrm{A}\).
Použijeme-li vztah z předešlého výpočtu, dostaneme
\[\mu_0 I = B\ 2 \pi r,\]kde, jak již bylo řečeno, \(I=0 \ \mathrm{A}\) a proto
\[B=0\ \mathrm{T}.\]Odpověď
a) Magnetická indukce ve vzdálenosti r od dlouhého přímého vodiče, kterým prochází proud I, je
\[B=\frac{\mu}{2\pi}\frac{I}{r}.\]b) Magnetická indukce ve vzdálenosti r \((r>R)\) od vodiče o poloměru R, kterým prochází proud I, je
\[B=\frac{\mu}{2\pi}\frac{I}{r}.\]Magnetická indukce uvnitř vodiče o poloměru R ve vzdálenosti r od středu vodiče (tj. pro \(R>r \)), kterým prochází proud I, je
\[B= \frac {\mu}{2\pi}\frac{rI}{R}.\]c) Magnetická indukce ve vzdálenosti r \((r>R_2>R_1)\) od středu dlouhé tlustostěnné trubky, kterou prochází proud I, je
\[B=\frac{\mu}{2\pi}\frac{I}{r}.\]Magnetická indukce ve vzdálenosti r \((R_2>r>R_1 )\) od dlouhé tlustostěnné trubky, kterou prochází proud I, je
\[B=\frac{\mu_0 I}{2\pi\left(R_2^{2}-R_1^{2}\right)}\frac{r^{2}-R_1^{2}}{r}.\]Magnetická indukce ve vzdálenosti r \((R_2>R_1>r) \) od dlouhé tlustostěnné trubky, kterou prochází proud I, je
\[B=0\ \mathrm{T}.\]

