Sbírka řešených úloh

Drátěný obdélník protékaný proudem

Úloha číslo: 796

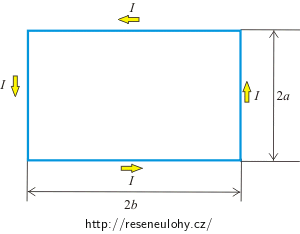
Určete, v jakém poměru musí být délky stran drátěného obdélníku daného obsahu S protékaného proudem I, aby magnetická indukce \(\vec{B}\) ve středu obdélníku byla maximální.

Poznámka: Velikosti stran uvažovaného obdélníku si označíte 2a a 2b.

• Nápověda 1

  Jak určíte magnetickou indukci ve středu obdélníku?

• Řešení nápovědy

  Magnetická indukce ve středu obdélníku je dána vektorovým součtem příspěvků od jednotlivých stran obdélníku. Příspěvek od jedné strany vlastně znamená spočítat magnetické pole v okolí úsečky s proudem. To je ukázáno v úloze Magnetické pole dlouhého přímého vodiče s proudem, Řešení 1.

• Nápověda 2

  Při určování směrů jednotlivých příspěvků k magnetické indukci použijte Ampérovo pravidlo pravé ruky.

• Ampérovo pravidlo pravé ruky

  Palec pravé ruky dáme tak, že ukazuje směr elektrického proudu ve vodiči. Pokrčené prsty pak ukazují orientaci magnetické indukce v okolí přímého vodiče.

• Rozbor

  Spočítáme magnetickou indukci ve středu obdélníku. Jde o vektorový součet magnetických indukcí od jednotlivých stran obdélníku. K určení jednotlivých směrů využijeme Ampérovo pravidlo a velikost spočítáme podle Biotova-Savartova zákona.

  Jakmile máme vztah pro velikost celkové indukce, můžeme přistoupit k hledání délek stran obdélníku pro maximální indukci za podmínky konstantního obsahu. Ze vztahu pro obsah obdélníku si vyjádříme jednu délku strany a dosadíme ji do vztahu pro velikost celkové magnetické indukce. Takto upravený výraz, kde už vystupuje pouze jedna neznámá, zderivujeme, abychom našli maximum.

• Řešení

  V první fázi určíme velikost magnetické indukce ve středu obdélníku jako funkci délek jeho stran. Celková indukce bude dána vektorovým součtem indukcí vyvolaných jednotlivými stranami. Pomocí Ampérova pravidla pravé ruky zjistíme, že všechny tyto vektory budou mít stejný směr nahoru kolmo k rovině obdélníku. Pro velikost celkové indukce ve středu pak bude platit vztah \[B=2\,B_\mathrm{a}+2\,B_\mathrm{b},\] kde B_a je velikost indukce vyvolané ve středu stranou délky 2a a B_b je velikost indukce vyvolané stranou délky 2b.

  Nejprve určíme B_a. Mohli bychom integrovat pomocí Biotova-Savartova zákona \[\mathrm{d}\vec{B}= \frac{\mu_{0}I}{4\pi}\cdot \frac{\mathrm{d} \vec{l}\times \vec{r}}{r^{3}},\] kde \(\mathrm{d}\vec{l}\) je element vodiče a \(\vec{r}\) je polohový vektor směřující od elementu vodiče do středu obdélníku.

  My ale využijeme toho, že v úloze Magnetické pole dlouhého přímého vodiče s proudem, Řešení 2 už máme provedený výpočet. Využíváme zde toho, že střed obdélníku leží na ose úsečky.

  Pro přehlednost uvedeme potřebný vztah, který si upravíme pro naše proměnné:

  \[B_\mathrm{a}=\frac{\mu_0I}{2\pi}\,\left[\frac{l}{b\sqrt{l^2+b^2}}\right]_0^\mathrm{a}=\frac {\mu_0 I a}{2\pi b \sqrt{a^{2}+b^{2}}}. \]

  Velikost magnetické indukce B_b je dána vztahem

  \[B_\mathrm{b}=\frac{\mu_0 I}{2 \pi }\cdot \left[ \frac {l}{a\sqrt{a^{2}+l^{2}}}\right]_{0} ^\mathrm{b} = \frac {\mu_0 I b}{2\pi a \sqrt{a^{2}+b^{2}}}. \]

  Dosadíme do vztahu pro velikost celkové magnetické indukce ve středu obdélníku

  \[ B=2 B_\mathrm{a} +2 B_\mathrm{b} = \frac{\mu_0 I a}{\pi b \sqrt{a^{2}+ b^{2}}}+ \frac{\mu_0 I b}{\pi a \sqrt{a^{2}+b^{2}}}=\frac{\mu_0 I}{\pi \sqrt{a^{2}+b^{2}}}\cdot \left(\frac{a}{b}+\frac{b}{a}\right)=\frac{\mu_0 I \sqrt{a^{2}+b^{2}}}{\pi a b}.\]

  Nyní budeme hledat rozměry obdélníku. Výraz pro celkovou magnetickou indukci si upravíme

  \[B= \frac{4\mu_0 I \sqrt{a^{2}+b^{2}}}{\pi 4 a b} = \frac{4\mu_0 I}{\pi S}\cdot \sqrt{a^{2}+b^{2}}, \]

  kde S = 4ab je obsah obdélníku, který je konstantní. K tomu, abychom dosáhli maximální indukce ve středu obdélníku, musíme nastavit jeho rozměry 2a a 2b tak, aby výraz \({a^{2}+b^{2}}\) byl co možná největší. Přitom však musíme respektovat podmínku, že máme pevně zadaný obsah obdélníku \( S=4ab\). Z této podmínky si vyjádříme neznámou b a dosadíme do předpisu funkce:

  \[ b=\frac{S}{4a}\qquad \Rightarrow \qquad y= a^{2} + \frac{S^{2}}{16 a^{2}}.\]

  Poté již získáme funkci jedné proměnné, jejíž extrém nalezneme tak, že ji zderivujeme, derivaci položíme rovnu nule a tím získáme rozměr 2a:

  \[\frac{\mathrm dy}{\mathrm da}=2a-\frac{S^{2}}{8a^{3}}=0 \] \[16a^{4}=S^{2}\] \[2a=\sqrt{S}.\]

  Pomocí druhé derivace bychom se přesvědčili, že jde skutečně o maximum. Zpětným dosazením zjistíme, jaký je rozměr strany 2b:

  \[S=4ab\qquad \Rightarrow \qquad 2b=\frac{S}{2a}=\frac{S}{\sqrt{S}}=\sqrt{S}.\]

• Odpověď

  Aby magnetická indukce ve středu obdélníku za daného obsahu S byla maximální, musí být strany v poměru 1:1, tzn. požadovaný obdélník je vlastně čtverec o straně, která má velikost \(\sqrt{S}\).