Pravoúhlá proudová smyčka
Úloha číslo: 2276
Určete magnetické pole v počátku soustavy souřadnic, které vytváří proudová smyčka o zadaných rozměrech, pokud jí protéká stálý proud I.
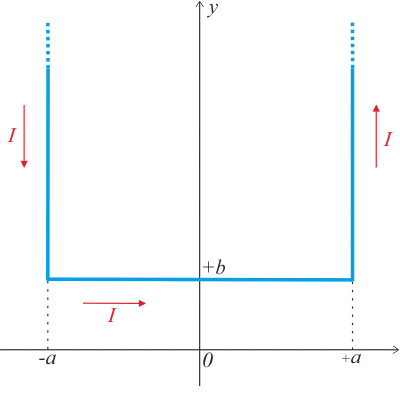
Nápověda
V řešení úlohy využijeme výsledků z úlohy Magnetické pole dlouhého přímého vodiče s proudem, pokud jste úlohu neřešili, doporučujeme si ji vyřešit a pak se vrátit k této úloze.
Z úlohy Magnetické pole dlouhého přímého vodiče s proudem, Odpověď využijeme vztah pro velikost magnetické indukce B, kterou v bodě P vytváří přímý vodič konečné délky, jímž protéká proud I
\[B=\frac{\mu_0}{4\pi}\frac{I}{R}(\cos\alpha-\cos\beta).\]Význam úhlů \(\alpha\) a \(\beta\) ilustruje následující obrázek a \(R\) označuje vzdálenost bodu P a přímky, na které vodič leží.
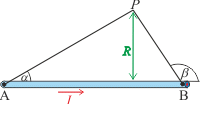
Uvědomte si, že magnetická indukce je vektorová veličina. Proto nemůžeme spočítat velikosti příspěvků od jednotlivých částí proudové smyčky a pak je sečíst. Musíme provést jejich vektorový součet, tedy uvažovat směry jednotlivých příspěvků.
Když umíme spočítat magnetickou indukci v okolí přímého vodiče, jakým způsobem rozdělíme zadaný vodič na části?
Nápověda – směry magnetické indukce od jednotlivých částí
K určení směru magnetické indukce od jednotlivých částí nám pomůže vzorec pro elementární příspěvek k magnetické indukci, tzv. Biotův-Savartův zákon (Magnetické pole dlouhého přímého vodiče s proudem, Řešení nápovědy):
\[\mathrm{d}\vec{B}=\frac{\mu_0}{4\pi}\frac{I\mathrm{d}\vec{x}\times\vec{r}}{r^3},\]kde \(\vec{x}\) je vektor ve směru protékajícího proudu v místě elementárního kousku drátu a \(\vec{r}\) je vektor spojující infinitezimální kousek drátu a bod, v němž magnetickou indukci počítáme. Výsledný směr určíme pomocí pravidla pravé ruky pro vektorový součin, kde ukazováček je ve směru \(\vec{x}\), prostředníček je ve směru \(\vec{r}\) a palec ukazuje výsledný směr magnetické indukce.
Jaké směry budou mít příspěvky od jednotlivých částí, na které jsme rozdělili zadaný vodič v předchozí nápovědě?
Řešení
Jak bylo řečeno v nápovědách, proudovou smyčku rozdělíme na tři části a výslednou magnetickou indukci v počátku soustavy souřadnic určíme jako součet příspěvků od každé části.

V nápovědě jsme si také připomněli, že pro velikost magnetické indukce v libovolném bodě P ve vzdálenosti R od přímého vodiče konečné délky platí
\[ B=\frac{\mu_0}{4\pi}\frac{I}{R}(\cos\alpha-\cos\beta).\tag{1}\]Tento vztah využijeme pro výpočet příspěvku magnetické indukce od každé z částí. Začněme levým svislým vodičem.
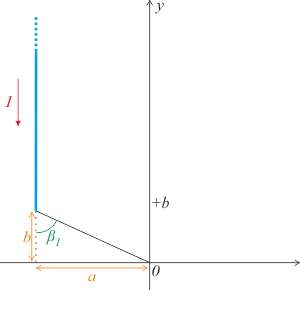
Nyní potřebujeme vyjádřit hodnoty \(\cos\alpha_1\) a \(\cos\beta_1\). Jelikož vodič pokračuje ve směru y do nekonečna, je zřejmé, že úhel \(\alpha_1=0°\) a tudíž
\[\cos\alpha_1=1.\tag{2}\]Hodnotu \(\cos\beta_1\) vyjádříme z pravoúhlého trojúhelníku na obrázku, v němž známe obě odvěsny a přeponu dopočítáme pomocí Pythagorovy věty:
\[\cos\beta_1=\frac{b}{\sqrt{a^2+b^2}}. \tag{3}\]Poslední hodnotu, kterou musíme vyjádřit, abychom mohli vztah použít, je vzdálenost R, což je v našem případě vzdálenost počátku soustavy souřadnic od pomyslné přímky procházející levou svislou částí vodiče neboli
\[ R_1=a.\tag{4}\]Dosazením (2), (3) a (4) do (1) dostaneme výsledný příspěvek od levé části proudové smyčky:
\[B_1=\frac{\mu_0}{4\pi}\frac{I}{a}\left(1-\frac{b}{\sqrt{a^2+b^2}}\right).\tag{A}\]Zřejmě platí, že velikost příspěvku od pravé svislé části proudové smyčky je stejná jako velikost příspěvku od svislé levé části:
\[B_2=\frac{\mu_0}{4\pi}\frac{I}{a}\left(1-\frac{b}{\sqrt{a^2+b^2}}\right).\tag{B}\]Nyní vypočteme příspěvek od prostřední části.

Zřejmě platí \(\omega + \beta_3 = \pi,\) z čehož dostaneme
\[\cos \omega = \cos (\pi-\beta_3).\]Jelikož je kosinus sudá funkce, můžeme upravit
\[\cos \omega = \cos (\beta_3-\pi),\]a tedy
\[\cos \omega = - \cos \beta_3.\]Když si uvědomíme, že \(\alpha_3 = \omega\), dostaneme
\[\cos \alpha_3 = - \cos \beta_3.\]Pomocí posledního vztahu upravíme vzorec (1) a získáme
\[ B=\frac{\mu_0}{2\pi}\frac{I}{R}\cos\alpha_3.\tag{5}\]Pomocí goniometrických funkcí vyjádříme
\[\cos\alpha_3=\frac{a}{\sqrt{a^2+b^2}}.\]Vzdálenost R je vzdálenost vodiče od počátku soustavy souřadnic neboli
\[R_3=b.\]Dosadíme-li poslední dva vztahy do rovnice (5), obdržíme
\[ B_3=\frac{\mu_0}{2\pi}\frac{I}{b}\frac{a}{\sqrt{a^2+b^2}}.\tag{C}\]Výslednou magnetickou indukci od proudové smyčky v počátku soustavy souřadnic získáme jako součet jednotlivých příspěvků:
\[\vec{B}=\vec{B}_1+\vec{B}_2+\vec{B}_3.\]Jak bylo pojednáno v nápovědě, směr příspěvku magnetické indukce od levé i pravé části je ven z nákresny a příspěvek od prostřední části je do nákresny, čímž dostaneme
\[B=B_1 + B_2 - B_3 = 2B_1 - B_3.\]Do posledního vztahu dosadíme výsledky (A), (B) a (C):
\[B=\frac{\mu_0}{2\pi}\frac{I}{a}\left(1-\frac{b}{\sqrt{a^2+b^2}}\right) - \frac{\mu_0}{2\pi}\frac{I}{b}\frac{a}{\sqrt{a^2+b^2}}, \] \[B=\frac{\mu_0}{2\pi}I\left(\frac{1}{a}-\frac{b}{a\sqrt{a^2+b^2}}-\frac{a}{b\sqrt{a^2+b^2}}\right),\] \[B=\frac{\mu_0}{2\pi}I\left(\frac{b\sqrt{a^2+b^2} -b^2-a^2}{ab\sqrt{a^2+b^2}}\right)=\frac{\mu_0}{2\pi}I\left(\frac{b -\sqrt{a^2+b^2}}{ab}\right).\]Odpověď
V počátku soustavy souřadnic působí výsledná magnetická indukce o velikosti
\[B=\frac{\mu_0}{2\pi}I\left(\frac{b -\sqrt{a^2+b^2}}{ab}\right)\]ve směru ven z nákresny.
Komentář – limitní případy
Zamysleme se nad speciálními případy geometrie pravoúhlé proudové smyčky a ověřme, že odvozený vztah jim odpovídá.
a) \(b=0\)Bude-li \(b=0\), potom střední část vodiče bude procházet počátkem soustavy souřadnic (místem, kde počítáme magnetickou indukci), a tudíž nebude přispívat k magnetické indukci (vektorový součin dvou rovnoběžných vektorů je nulový). K magnetické indukci budou přispívat pouze dvě polopřímky. Výsledné magnetické pole bude mít velikost \(B=\frac{\mu_0}{2\pi}\frac{I}{a}\) a jeho směr bude ven z nákresny. Vztah odpovídá velikosti magnetické indukce v okolí nekonečně dlouhého přímého vodiče, což souhlasí s naší situací, protože na dva nekonečně dlouhé polopřímkové vodiče v naší úloze je možné se dívat jako na nekonečně dlouhý přímý vodič. Ověřme tuto úvahu i poctivým vypočítáním limity.
Pozn.: Pokud je \(b=0\), pak střední část vodiče prochází bodem, ve kterém počítáme magnetickou indukci. V takovém případě ale pro střední část vodiče nemůžeme použít Biotův-Savartův zákon (výpočet by nám dal nekonečno díky „nule“ ve jmenovateli). Proto musíme limitu spočítat pouze pro příspěvky svislých vodičů:
\[\lim_{b \to 0}\frac{\mu_0}{2\pi}\frac{I}{a}\left(1-\frac{b}{\sqrt{a^2+b^2}}\right)=\frac{\mu_0}{2\pi}\frac{I}{a}. \] b) \(b\to \infty\)Půjde-li b do nekonečna, pak bude pravoúhlá smyčka nekonečně vzdálená od počátku soustavy souřadnic, a tudíž \(B=0\space \mathrm{T}.\) Ověřme tuto úvahu vypočítáním limity.
\[\lim_{b \to \infty}\frac{\mu_0}{2\pi}I\left(\frac{b -\sqrt{a^2+b^2}}{ab}\right)=\frac{\mu_0}{2\pi}I\lim_{b \to \infty}\left(\frac{b\left(1 -\sqrt{\frac{a^2}{b^2}+1}\right)}{ab}\right) =0.\] c) \(a=0\)Bude-li \(a=0\), pak pravoúhlá proudová smyčka splyne do dvou polopřímek. Jelikož splývající polopřímky leží na přímce procházejí počátkem soustavy souřadnic, bude výsledné magnetické pole nulové. Stejně jako v a) si můžeme dva nekonečné polopřímkové vodiče s opačnými proudy představit jako nekonečný přímý vodič. Tento přímý vodič prochází bodem, ve kterém počítáme magnetickou indukci, a tudíž musí být magnetická indukce nulová. Ke stejnému závěru dojdeme, když si uvědomíme, že magnetická pole od obou vodičů se navzájem vyruší (výsledné pole bude nulové), jelikož vodiče leží na sobě a proudy tečou opačnými směry. Ověřme tyto úvahy vypočítáním limity:
\[\lim_{a \to 0}\frac{\mu_0}{2\pi}I\left(\frac{b -\sqrt{a^2+b^2}}{ab}\right)=\lim_{a \to 0}\frac{\mu_0}{2\pi}I\left(\frac{(b -\sqrt{a^2+b^2})(b +\sqrt{a^2+b^2})}{ab(b +\sqrt{a^2+b^2})}\right)=\] \[=\frac{\mu_0}{2\pi}I\lim_{a \to 0}\left(\frac{b^2-a^2-b^2}{ab(b +\sqrt{a^2+b^2})}\right)=\frac{\mu_0}{2\pi}I\lim_{a \to 0}\left(\frac{-a}{b(b +\sqrt{a^2+b^2})}\right)=0.\] d) \(a\to \infty\)Pokud a půjde do nekonečna, pak se pravoúhlá proudová smyčka přemění v přímku. Vzoreček pro velikost magnetického pole od přímky nalezneme v úloze Magnetické pole dlouhého přímého vodiče. Ověřme tuto úvahu vypočítáním limity:
\[\lim_{a \to \infty}\frac{\mu_0}{2\pi}I\left(\frac{b -\sqrt{a^2+b^2}}{ab}\right)=\frac{\mu_0}{2\pi}I\lim_{a \to \infty}\left(\frac{\frac{b}{a} -\sqrt{1+\frac{b^2}{a^2}}}{b}\right) =-\frac{\mu_0}{2\pi}\frac{I}{b}.\]Záporné znaménko nám říká, že směr magnetické indukce bude opačný, než je tomu v nelimitním případě. Magnetická indukce bude mít tudíž směr do nákresny, což také odpovídá Ampérovu pravidlu pravé ruky.

