Energie magnetického pole solenoidu
Úloha číslo: 66
Solenoid délky 80 cm a poloměru 5 cm má 3 000 rovnoměrně navinutých závitů. Jeho celkový odpor je 10 Ω. V čase 5 ms po připojení ke zdroji 12 V určete:
a) jakou energii má jeho magnetické pole,
b) jaká energie byla dodána zdrojem během této doby?
V části a) nejprve odvoďte vztah pro velikost energie magnetického pole solenoidu.
Nápověda
Nakreslete si obvod se zdrojem napětí, cívkou a rezistorem, který nahrazuje odpor solenoidu a přívodních vodičů. Pomocí 2. Kirchhoffova zákona sestavte diferenciální rovnici pro okamžité napětí. Protože potřebujeme znát rovnici pro energii nebo výkon, vynásobte diferenciální rovnici veličinou proudu.
Rozbor
Odvození vztahu pro energii magnetického pole solenoidu
Pro odvození vztahu pro energii magnetického pole solenoidu si nakreslíme obvod se zdrojem napětí, cívkou a rezistorem (který nahrazuje odpor vodičů v obvodu) a použijeme 2. Kirchhoffův zákon (smyčkové pravidlo) pro součet napětí v obvodu. Vzniklou rovnici vynásobíme proudem a získáme tak rovnici vyjadřující zákon zachování energie, kde každý člen má význam výkonu jednotlivých součástek v obvodu. Pro určení vztahu pro energii magnetického pole solenoidu využijeme člen odpovídající „výkonu“ magnetického pole, tj. časové změně energie magnetického pole.
Určení energie magnetického pole solenoidu
Pro určení energie magnetického pole solenoidu využijeme odvozený vztah pro velikost energie magnetického pole cívky. Do tohoto vztahu je potřeba dosadit okamžitou hodnotu proudu, který prochází solenoidem.
Solenoid vytváří v obvodu indukované elektromotorické napětí. Podle Lenzova zákona toto napětí brání změně, která ho vyvolala, tedy brání růstu proudu. To znamená, že indukované napětí má opačnou polaritu než baterie a proud díky tomu roste postupně. Později, po dosažení ustáleného stavu, kdy obvodem teče konstantní proud, se solenoid chová již jako obyčejný vodič. Musíme tedy nejprve vyjádřit, jak se okamžitý proud mění v čase, a potom dosadit do vztahu pro energii magnetického pole hodnotu okamžitého proudu v zadaném čase.
Energie dodaná zdrojem
Pro určení energie, která je do obvodu dodána zdrojem za určitý časový interval, vyjdeme z rovnice zachování energie v obvodu (použité při odvozování energie magnetického pole). Okamžitý výkon se rovná derivaci energie dodané zdrojem podle času, výraz pro výkon zdroje zintegujeme (podle času) a získáme tak vztah pro energii, která byla do obvodu dodána zdrojem za určitý časový interval.
Odvození vztahu pro energii magnetického pole solenoidu
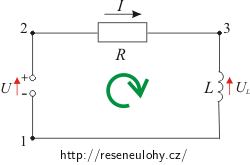
Nejdříve si nakreslíme obvod se zdrojem napětí U, rezistorem o odporu R a cívkou s indukčností L.
Sestavíme rovnici pro okamžitá napětí v tomto obvodu pomocí 2. Kirchhoffova zákona. Začneme v bodě 1 a postupujeme podél obvodu ve směru otáčení hodinových ručiček. Pro vyznačený směr proudu zaznamenáváme při průchodu baterií nárůst potenciálu o +U. Na rezistoru dochází k úbytku napětí o hodnotu −IR. Bod 3 má vyšší potenciál než bod 1, protože při rostoucím proudu brání indukované napětí tomuto růstu, a proto má indukované napětí UL směr vyznačený na obrázku. Když tedy přecházíme podél cívky z bodu 3 do bodu 1, změní se potenciál o
\[U_\mathrm{L}=-L\frac{\mathrm{d}I}{\mathrm{d}t}.\]2. Kirchhoffův zákon nám tedy dává:
\[U-IR-L\frac{\mathrm{d}I}{\mathrm{d}t}=0,\]po úpravě:
\[U=IR+L\frac{\mathrm{d}I}{\mathrm{d}t},\]což je diferenciální rovnice popisující časový vývoj proudu v tomto obvodu. V této rovnici I označuje okamžitou hodnotu proudu a U okamžitou hodnotu napětí zdroje, obě veličiny mohou být časově závislé.
Protože chceme odvodit vztah pro energii magnetického pole cívky, vynásobíme obě strany rovnice veličinou I:
\[UI=I^2R+LI\frac{\mathrm{d}I}{\mathrm{d}t},\tag{1}\]protože tím člen na levé straně rovnice představuje výkon, s jakým zdroj napětí dodává energii do zbytku obvodu. Dále první člen na pravé straně rovnice představuje rychlost, s níž se přeměňuje energie v rezistoru na teplo, tj. tepelný výkon rezistoru.
Energie, která není v rezistoru přeměněna na teplo, se hromadí v magnetickém poli cívky. Rovnice (1) tedy vyjadřuje zákon zachování energie v tomto obvodu a třetí člen tedy představuje „rychlost“ dEl/dt hromadění energie v magnetickém poli (přesněji časovou změnu energie magnetického pole cívky), tedy:
\[\frac{\mathrm{d}E_\mathrm{l}}{\mathrm{d}t}=LI\,\frac{\mathrm{d}I}{\mathrm{d}t}.\]Rovnici zintegrujeme v čase:
\[\int\mathrm{d}E_\mathrm{l}=\int LI\,\mathrm{d}I.\]Pro velikost magnetické energie El magnetického pole cívky, kterou teče proud I, dostáváme vztah:
\[E_\mathrm{l}=\frac{1}{2}\,LI^2.\]Řešení a) Energie magnetického pole solenoidu
Pro určení energie magnetického pole solenoidu vyjdeme ze vztahu pro energii cívky, který jsme odvodili v předchozím oddíle:
\[E_\mathrm{l}=\frac{1}{2}\,LI^2.\]Pro výpočet energie magnetického pole potřebujeme znát okamžitý proud I procházející cívkou v daném čase. Kdyby v obvodu cívka nebyla, vzrostl by proud okamžitě po připojení napětí. Cívka však vytváří v obvodu indukované elektromotorické napětí, které brání změně, která ho vyvolala, tedy brání růstu proudu.
Velikost proudu I v závislosti na čase (po připojení cívky na stejnosměrný zdroj napětí o konstantní velikosti U) je dána vztahem:
\[I = \frac{U}{R}\,\left(1-e^{-\frac{R}{L}t}\right),\]kde R je odpor solenoidu a L jeho indukčnost. Tento vztah je podrobně odvozen v úloze Energie a výkon magnetického pole cívky.
Pro indukčnost L solenoidu platí vztah odvozen v úloze Indukčnost cívky rotující v magnetickém poli:
\[L=\mu_\mathrm{0}\frac{N^2S}{l},\]kde N je počet závitů solenoidu, l je jeho délka a pro pruřez S solenoidu platí S = πr2.
Pro indukčnost solenoidu tak dostáváme výraz:
\[L=\frac{\mu_\mathrm{0}\pi N^2 r^2}{l}.\]Po dosazení proudu I do rovnice pro energii magnetického pole cívky El dostáváme
\[E_\mathrm{l}=\frac{1}{2}\,\frac{LU^2}{R^2}\,\left(1-e^{-\frac{R}{L}t}\right)^{2}.\]Poznámka: Pro přehlednost jsme do vztahu pro energii solenoidu nedosadili vztah pro indukčnost L, který vypočítáme zvlášť a do vzorce dosadíme jen jeho konkrétní hodnotu.
Řešení b) Energie dodaná zdrojem napětí
Energii, která byla dodána zdrojem za daný čas, určíme pomocí výkonu zdroje, který tuto energii dodává.
Výkon P je definován jako rychlost přenosu dodané energie Ez za čas:
\[P=\frac{\mathrm{d}E_\mathrm{z}}{\mathrm{d}t}.\]Rovnici upravíme:
\[ \mathrm{d}E_\mathrm{z}=P\, \mathrm{d}t.\]Výkon, s jakým je dodávána energie Ez zdrojem do obvodu, představuje člen na levé straně rovnice (1) pro zachování energie v obvodu (viz oddíl Odvození energie magnetického pole):
\[UI=I^2R+LI\frac{\mathrm{d}I}{\mathrm{d}t}.\tag{1}\]Dostáváme tak výraz:
\[ \mathrm{d}E_\mathrm{z}=UI\, \mathrm{d}t,\tag{2}\]kde proud I, který obvodem prochází, není konstantní. Pro jeho velikost v čase t platí:
\[I = \frac{U}{R}\,\left(1-e^{-\frac{R}{L}t}\right).\]Výraz pro okamžitou hodnotu proudu dosadíme do rovnice (2):
\[ \mathrm{d}E_\mathrm{z}= \frac{U^2}{R}\,\left(1-e^{-\frac{R}{L}t_1}\right)\, \mathrm{d}t.\]Výraz na levé straně budeme integrovat v časovém intervalu:
\[\int_0^\mathrm{E_z} \mathrm{d}E_\mathrm{z}=\int_{0}^\mathrm{t} \frac{U^2}{R}\,\left(1-e^{-\frac{R}{L}t}\right)\, \mathrm{d}t.\]Po úpravě získáváme:
\[E_\mathrm{z}=\int_{0}^\mathrm{t} \frac{U^2}{R}\,- \frac{U^2}{R} e^{-\frac{R}{L}t}\, \mathrm{d}t,\] \[E_\mathrm{z}=\left[\frac{U^2}{R}t\,+\,\frac{U^2L}{R^2}\,e^{-\frac{R}{L}t}\right]_{0}^\mathrm{t}.\]Do výrazu dosadíme integrační meze. Pro energii Ez tak získáváme výraz:
\[E_\mathrm{z}=\frac{U^2}{R}t\,+\,\frac{U^2L}{R^2}\,e^{-\frac{R}{L}t}-\,\frac{U^2L}{R^2},\] \[E_\mathrm{z}=\frac{U^2}{R}\,\left[\frac{L}{R}(\,e^{-\frac{R}{L}t}-1)+t\right].\]Pro indukčnost solenoidu L platí vztah:
\[L=\frac{\mu_\mathrm{0}\pi N^2 r^2}{l},\]který pro přehlednost není do výrazu dosazen. V oddíle Zápis a číselné dosazení je nejdříve vyjádřena jeho konkrétní hodnota, která je pak do vztahu pro energii zdroje Ez dosazena.
Zápis a číselné dosazení
\(l\,=\,80\,\mathrm{cm}=\,0{,}8\,\mathrm{m}\) délka solenoidu \(r\,=\,5\,\mathrm{cm}=\,0{,}05\,\mathrm{m}\) poloměr solenoidu \(R\,=\,10\,\mathrm{\Omega}\) odpor solenoidu \(n\,=\,3000\) počet závitů solenoidu \(t\,=\,5{\cdot}10^{-3}\,\mathrm{s}\) doba připojení solenoidu ke zdroji \(U\,=\,12\,\mathrm{V}\) napětí zdroje \(E_\mathrm{l}\,=\mathrm{?}\,\mathrm{(J)}\) energie mg. pole solenoidu \(E_\mathrm{z}\,=\mathrm{?}\,\mathrm{(J)}\) energie dodaná zdrojem Z tabulek: \(\mu_\mathrm{0}=4\pi \cdot 10^{-7}\,\mathrm{Hm^{-1}}\) permeabilita vakua
Výpočet indukčnosti L:
\[L=\frac{\mu_\mathrm{0}\pi N^2 r^2}{l}=\frac{4\pi^2 {\cdot} 10^{-7}\cdot3000^2{\cdot}0{,}05^2}{0{,}8}\,\mathrm{H}\,\dot{=}\,0{,}1\,\mathrm{H}\]Výpočet energie El magnetického pole solenoidu:
\[E_\mathrm{l}=\frac{1}{2}\,\frac{LU^2}{R^2}\,\left(1-e^{-\frac{R}{L}t}\right)^{2}\] \[E_\mathrm{l}=\frac{1}{2}\cdot\,\frac{0{,}1{\cdot}12^2}{10^2}\cdot\left(1-e^{-\frac{10}{0{,}1}\cdot5{\cdot}10^{-3}}\right)^{2}\,\mathrm{mJ}\] \[E_\mathrm{l}\,\dot{=}\,0{,}011\,\mathrm{J}=11\,\mathrm{mJ}.\]Výpočet energie Ez dodané zdrojem:
\[E_\mathrm{z}=\frac{U^2}{R}\,\left[\frac{L}{R}(\,e^{-\frac{R}{L}t}-1)+t\right]\] \[E_\mathrm{z}=\frac{12^2}{10}\cdot\,\left[\frac{0{,}1}{10}\cdot(\,e^{-\frac{10}{0{,}1}\cdot5{\cdot}10^{-3}}-1)+5{\cdot}10^{-3}\right]\,\mathrm{J}\] \[E_\mathrm{p}\,\dot{=}\,0{,}014\,\mathrm{J}=14\,\mathrm{mJ}.\]Odpověď
Magnetické pole solenoidu má v čase 5 ms energii přibližně El = 11 mJ.
Během 5 ms byla zdrojem dodána energie přibližně Ez = 14 mJ.