Smyčka vzdalující se od vodiče
Úloha číslo: 61
Pevná kovová obdélníková smyčka o rozměrech 5 cm a 10 cm, se vzdaluje od dlouhého přímého vodiče s proudem o velikosti 3 A rychlostí 4 m s-1. Rychlost je kolmá k vodiči. Dvě protilehlé strany a vodič zůstávají neustále rovnoběžné a v jedné rovině. Určete velikost indukovaného elektromotorického napětí ve smyčce v okamžiku, kdy vzdálenost bližší strany od vodiče je 2 cm.
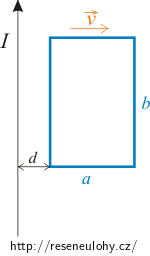
Nápověda
Rozmyslete si, jak vypadá vzorec pro elektromotorické napětí indukované ve vodivé smyčce. Co platí pro magnetický indukční tok procházející smyčkou?
Rozbor
Velikost elektromotorického napětí indukovaného ve vodivé smyčce je rovna rychlosti změny magnetického indukčního toku procházejícího plochou této smyčky.
Změnu magnetického toku si vyjádříme jako rozdíl počátečního a koncového magnetického toku smyčkou při jejím malém posunutí ze zadané polohy.
Magnetické indukční toky si vyjádříme jako součet toku Φ,, který je společný pro obě polohy smyčky, a toků dΦ1 a dΦ2, o které se smyčky liší.
Obrázek
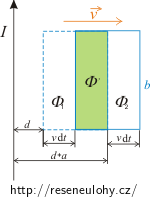
Pozn.: Jedná se o infinitizimálně malé posunutí vodiče. Pro lepší přehlednost je posunutí v obrázku přehnané.
Řešení
Velikost elektromotorického napětí indukovaného ve vodivé smyčce se rovná rychlosti změny magnetického indukčního toku procházejícího vodivou smyčkou:
\[U_\mathrm{i}=-\frac{\mathrm{d} \Phi}{\mathrm{d}t}.\]Za dΦ dosadíme rozdíl toků smyčkou v počáteční a koncové poloze:
\[\mathrm{d}\Phi = \Phi_1 -\Phi_2.\]Jednotlivé magnetické indukční toky si vyjádříme jako součet toku Φ,, který je společný pro obě polohy smyčky, a toků dΦ1 a dΦ2, o které se obě polohy liší:
\[\Phi_1 = \Phi^, + \mathrm{d}\Phi_{1}\] \[\Phi_2 = \Phi^, + \mathrm{d}\Phi_{2}.\]Protože se při odčítání toků v počáteční a koncové poloze odečte „společný tok“ Φ,, vyjádříme si jen toky dΦ1 a dΦ2. Vzhledem k tomu, že plošky, kterými počítáme tok, jsou úzké, můžeme předpokládat, že se v nich nemění velikost magnetické indukce B. Potom pro magnetický indukční tok platí obecný vztah:
\[\Phi =BS\cos\alpha,\]kde úhel α je úhel mezi kolmicí na plochu a indukčními čarami. V našem případě je α = 0°, tedy cos α = 1.
Za velikost magnetické indukce B dosadíme vztah pro magnetickou indukci v okolí dlouhého přímého vodiče
\[B=\frac{\mu_0}{2\pi}\frac{I}{d}.\]S je obsah plochy, která ohraničuje magnetický indukční tok. V našem případě je plocha pro dΦ1 i dΦ2 stejná a platí (viz obrázek):
\[S = b v \mathrm{d}t.\]Po dosazení jednotlivých vztahů do rovnic pro Φ1 a Φ2 dostáváme:
\[\Phi_1 = \Phi^, + \,\frac{\mu_0}{2\pi}\frac{I}{d}\,b\,v\,\mathrm{d}t\] \[\Phi_2 = \Phi^, + \,\frac{\mu_0}{2\pi}\frac{I}{d+a}\,b\,v\,\mathrm{d}t.\]Po odečtení toků v počáteční a koncové poloze:
\[\mathrm{d}\Phi = \frac{\mu_0 Ibvdt}{2\pi} \left(\frac{1}{d}-\frac{1}{d+a}\right).\]Nyní již můžeme vyjádřenou změnu indukčního toku dosadit do vzorce pro elektromotorické napětí:
\[U_\mathrm{i} = \frac{\mu_0 Ibvdt}{2\pi dt} \left(\frac{1}{d}-\frac {1}{d+a}\right).\]Po matematické úpravě dostáváme:
\[U_\mathrm{i} = \frac{\mu_0 Ibv}{2\pi}\, \frac{a}{d(d+a)}.\]Zápis a číselné dosazení
\(v=4 \,\mathrm{ms^{-1}}\) rychlost vzdalování obdélníkové smyčky \(a = 5\,\mathrm{cm}=0{,}05 \,\mathrm{m}\) první rozměr obdélníkové smyčky \(b=10\,\mathrm{cm}=0{,}10 \,\mathrm{m} \) druhý rozměr obdélníkové smyčky \(d = 2\,\mathrm{cm}=0{,}02 \,\mathrm{m}\) vzdálenost obdélníkové smyčky od přímého vodiče \(I = 3\,\mathrm{A}\) proud tekoucí přímým vodičem \(|U_i| = \mathrm{?}\,\mathrm{(V)}\) velikost indukovaného elektromotorického napětí ve smyčce
\[|U_i| = \frac{\mu_0 Ibv}{2\pi}\, \frac{a}{d(d+a)}= \frac{4\cdot \pi \cdot 10^{-7} \cdot3{\cdot}0{,}1{\cdot} 4}{2\pi}\,\cdot \frac{0{,}05}{0{,}02\cdot(0{,}02+0{,}05)}\,\mathrm{V} = 8{,}6\,\mathrm{\mu V}\]Odpověď
Při oddalování smyčky od vodiče se bude v daném místě ve smyčce indukovat elektromotorické napětí Ui = 8,6 μV.
Komentář - Řešení pomocí celkového toku smyčkou
Magnetický indukční tok plochou smyčky je definován:
\[\Phi=\int{\vec{B}\cdot\,\mathrm{d}\vec{S}}.\]Jelikož vektor magnetické indukce je kolmý na plochu smyčky, můžeme integrál psát ve tvaru:
\[\Phi=\int{B}\,\mathrm{d}S.\]Za velikost magnetické indukce B dosadíme vztah pro magnetickou indukci dlouhého přímého vodiče ve vzdálenosti x od vodiče:
\[B = \frac{\mu_0 I}{2\pi x}.\]Protože se vzdálenost vodiče a místa, ve kterém určujeme magnetický indukční tok, mění, zvolíme ji jako proměnnou, kterou budeme integrovat. Element plochy dS si vyjádříme pomocí proměnné vzdálenosti jako: dS = b dx.
Meze, ve kterých se pohybuje vzdálenost od vodiče a ve kterých budeme integrovat, jsou vzdálenosti obou stran smyčky od vodiče. Magnetický indukční tok si tedy můžeme vyjádřit jako:
\[\Phi=\int_\mathrm{d}^\mathrm{d+a}{\frac{\mu_0}{2\pi}\,\frac{I}{x}\,b\,\mathrm{d}x}.\]Konstanty vytkneme před integrál:
\[\Phi=\frac{\mu_0Ib}{2\pi}\,\int_\mathrm{d}^\mathrm{d+a}{\frac{1}{x}}\,\mathrm{d}x.\]Po jednoduché integraci a dosazení integračních mezí dostáváme:
\[\Phi=\frac{\mu_0Ib}{2\pi}\,\left[\mathrm{ln}\,x \right]_\mathrm{d}^\mathrm{d+a}=\frac{\mu_0Ib}{2\pi}\, \mathrm{ln}\frac{d+a}{d}.\]Úkolem je určit velikost indukovaného elektromotorického napětí. To vyjádříme jako derivaci magnetického indukčního toku podle času:
\[U_\mathrm{i} = -\frac{\mathrm{d}\Phi}{\mathrm{d}t} = -\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mu_0Ib}{2\pi}\, \mathrm{ln}\frac{d+a}{d}\right).\]Na čase t závisí pouze proměnná d. Protože se smyčka vzdaluje rovnoměrně, můžeme ji vyjádřit jako:
\[d(t)=vt.\]Po dosazení do vzorce pro indukované napětí a vytknutí konstant nezávislých na čase před derivací dostáváme výraz:
\[U_\mathrm{i} = -\frac{\mu_0Ib}{2\pi}\,\frac{\mathrm{d}}{\mathrm{d}t}\left(\mathrm{ln}\frac{vt+a}{vt}\right).\]Po zderivování funkce logaritmus, která obsahuje vnitřní funkci (vt+a)/(vt), dostáváme výraz:
\[U_\mathrm{i} = -\frac{\mu_0Ib}{2\pi}\,\frac{vt}{vt+a}\,\frac{-av}{(vt)^{2}},\]který dále upravíme:
\[U_\mathrm{i} = \frac{\mu_0Ib}{2\pi}\,\frac{1}{vt+a}\,\frac{a}{t}.\]Za čas t dosadíme okamžik, kdy smyčka dosáhne požadované vzdálenosti, tj.:
\[t =\frac{d}{v}\] \[U_\mathrm{i} = \frac{\mu_0Ib}{2\pi}\,\frac{1}{d+a}\,\frac{av}{d} = \frac{\mu_0Ib}{2\pi}\,\frac{av}{d(d+a)}.\]Velikost indukovaného napětí ve smyčce vyšla stejně, i když jsme počítali jiným způsobem.



