Sbírka řešených úloh

Jaké teplo spirála předala?

Úloha číslo: 1665

• Rozbor

  Eva při měření předpokládala, že stejnosměrný zdroj dává konstantní napětí. Pokud by tomu tak bylo, pak by naměřené hodnoty napětí a proudu byly hodnotami efektivními a bylo by vše v pořádku.

  Zdroj však poskytoval pouze dvoucestně usměrněný harmonický průběh (bez filtrace), viz obrázek.

  

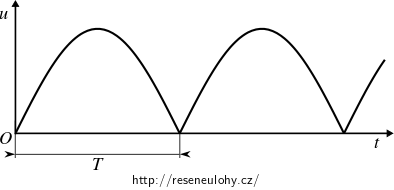
  Měřící přístroje na stejnosměrných rozsazích obvykle ukazují hodnoty střední. Tyto střední hodnoty Eva dosadila do vztahu, který je určen pro hodnoty efektivní.

  Abychom zjistili, o kolik při výpočtu předaného tepla chybila, vypočítáme pro průběh na obrázku výše postupně

  • střední hodnoty napětí (a proudu),
  • efektivní hodnoty napětí (a proudu),
  • správné teplo předané spirálou vodě

  a toto teplo porovnáme s chybně určeným teplem Evou.

• Nápověda 1 – střední hodnoty

  Vypočtěte střední hodnotu napětí a proudu.

  Střední hodnotu napětí počítáme jako

  \[ \bar{u} = \frac{1}{T}\int_0^T u(t)\,\mathrm{d}t. \]

• Řešení nápovědy 1 – střední hodnoty

  Spirála je napájena dvoucestně usměrněným harmonickým napětím, tj. napětím o průběhu

  

  s parametrizací

  \[ u(t) = u_0 |\sin \omega t|, \]

  kde \(u_0\) značí maximální hodnotu napětí.

  Úhlové periodě \(\pi\) odpovídá časová perioda průběhu

  \[ T = \frac{\pi}{\omega}. \]

  Vypočítáme střední hodnotu napětí

  \[ \bar{u} = \frac{1}{T}\int_0^T u(t)\,\mathrm{d}t = \frac{1}{\pi/\omega}\int_0^{\pi/\omega} u_0 |\sin\omega t| \,\mathrm{d}t = \frac{u_0 \omega }{\pi}\int_0^{\pi/\omega}\sin\omega t \,\mathrm{d}t = \] \[ = \frac{u_0 \omega }{\pi} \left[-\frac{\cos \omega t}{\omega} \right]_0^{\pi/\omega}= \frac{u_0 \omega }{\pi} \frac{2}{\omega} = \frac{2}{\pi}u_0. \]

  Máme tedy

  \[ \bar{u} = \frac{2}{\pi}u_0. \tag{1}\]

  podobně pro střední hodnotu proudu

  \[ \bar{i} = \frac{2}{\pi}i_0, \tag{2}\]

  kde \(i_0\) značí maximální hodnotu proudu.

• Nápověda 2 – efektivní hodnoty

  Vypočtěte efektivní hodnotu napětí a proudu.

  Efektivní hodnotu napětí počítáme jako

  \[ U_\mathrm{ef} = \sqrt{\frac{1}{T}\int_0^T u^2(t)\,\mathrm{d}t}. \]

• Řešení nápovědy 2 – efektivní hodnoty

  Dvoucestně usměrněný harmonický průběh

  

  má parametrizaci \[ u(t) = u_0 |\sin \omega t|. \]

  Úhlové periodě \(\pi\) odpovídá časová perioda průběhu \(T = \frac{\pi}{\omega}.\)

  Nyní vypočítáme efektivní hodnotu napětí \[ U_\mathrm{ef} = \sqrt{\frac{1}{T}\int_0^T u^2(t)\,\mathrm{d}t} = \sqrt{\frac{\omega u_0^2}{\pi}\int_0^{\pi/\omega} \sin^2 \omega t \,\mathrm{d}t}= \]

  Integrál pod odmocninou vypočítáme zvlášť užitím goniometrické identity \(\color{MidnightBlue}{\sin^2 \alpha = \frac{1}{2}\left(1-\cos 2\alpha\right)}\):

  \[ \color{MidnightBlue}{ \int_0^{\pi/\omega} \sin^2 \omega t \,\mathrm{d}t = \int_0^{\pi/\omega} \frac{1}{2}\left(1-\cos 2\omega t\right)\,\mathrm{d}t = } \] \[ \color{MidnightBlue}{ = \frac{1}{2}\left[t - \frac{\sin 2\omega t}{2\omega}\right]_0^{\pi/\omega} = \frac{\pi}{2\omega}. } \]

  \[ = \sqrt{\frac{\omega u_0^2}{\pi} \frac{\pi}{2\omega} } = \frac{u_0}{\sqrt{2}}. \] Máme tedy \[ U_\mathrm{ef} = \frac{u_0}{\sqrt{2}}. \tag{3}\] Podobně efektivní hodnota proudu \[ I_\mathrm{ef} = \frac{i_0}{\sqrt{2}}. \tag{4}\]

• Nápověda 3 – porovnání tepel

  Určete správné teplo, které bylo spirálou za čas \(t\) vodě předáno a porovnejte s chybným výpočtem Evy.

• Řešení nápovědy 3 – porovnání tepel

  Spirála se chová jako rezistor, proud a napětí je tedy ve fázi a pro výkon lze psát \[P = U_\mathrm{ef}I_\mathrm{ef}.\] Za čas \(t\) předá spirála vodě teplo \[ Q_\mathrm{spravne}= U_\mathrm{ef}I_\mathrm{ef} t. \] Dosaďme za efektivní hodnoty z (3), (4) \[ Q_\mathrm{spravne}= \frac{u_0}{\sqrt{2}}\frac{i_0}{\sqrt{2}}t =\frac{1}{2} u_0 i_0 t. \] Maximální hodnoty vyjádříme pomocí hodnot středních z (1), (2) \[ Q_\mathrm{spravne} = \frac{1}{2} \left(\frac{\pi}{2}\bar{u}\right) \left(\frac{\pi}{2}\bar{i}\right) t = \frac{\pi^2}{8} \bar{u}\bar{i} t. \tag{5}\] Eva dosazovala do vztahu pro efektivní hodnoty hodnoty střední, vypočítala tak chybné teplo \[ Q_\mathrm{chybne} = \bar{u}\bar{i} t. \tag{6}\] Porovnáním (5) a (6) máme \[ Q_\mathrm{spravne} = \frac{\pi^2}{8} Q_\mathrm{chybne} \,\doteq\, 1{,}23\, Q_\mathrm{chybne}. \] Reálně předané teplo je oproti Evině chybnému výpočtu cca o \(23\,\%\) větší.

• Odpověď

  Reálně předané a chybně určené teplo jsou ve vztahu \[ Q_\mathrm{spravne} = \frac{\pi^2}{8} Q_\mathrm{chybne} \,\doteq\, 1{,}23\, Q_\mathrm{chybne}. \] Tj. reálně předané teplo je oproti chybnému výpočtu cca o \(23\,\%\) větší.