Sbírka řešených úloh

Kotva

Úloha číslo: 209

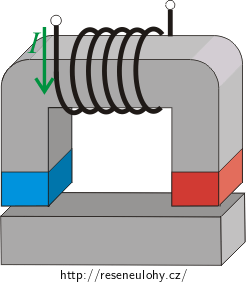
Kotva z oceli přiléhá k U-jádru z téhož materiálu. Na jádru je navinuta cívka se 600 závity. Průřez jádra je 6,25 cm², délka střední siločáry 50 cm a relativní permeabilita oceli μ_r = 1200. Jaký proud musí protékat cívkou, aby kotva byla držena silou 500 N?

Poznámka: Při odtržení kotvy od jádra uvažujte permeabilitu pole ve vzduchové mezeře rovnu permeabilitě vakua.

• Nápověda

  Síla, kterou je kotva držena k jádru, se rovná síle, kterou musíme vynaložit, abychom kotvu odtrhli. Při malém vzdalování kotvy se práce vnějších sil projeví jako přírůstek energie magnetického pole.

• Rozbor

  Abychom mohli odtrhnout kotvu od jádra cívky, musíme vykonat práci, která je rovna přírůstku energie uložené v magnetickém poli.

  Práce, kterou vykonáme při odtahování kotvy od jádra, se rovná práci síly, kterou působíme po malé dráze. Energie uložená v magnetickém poli cívky je rovna hustotě energie magnetického pole ve vzduchové mezeře, která vznikne posunutím kotvy.

• Řešení

  Při odtržení kotvy od jádra cívky musíme vykonat práci dW, která je rovna energii dE uložené v magnetickém poli vzniklé vzduchové mezery o šířce dx:

  $$\mathrm{d}W=\mathrm{d}E.$$

  Práci si vyjádříme jako sílu $\vec{F}$, kterou působíme ve stejném směru po malé dráze dx. Energii pak vyjádříme pomocí hustoty energie magnetického pole w v malém objemu dV:

  $$F\mathrm{d}x=w\mathrm{d}V.\tag{1}$$

  Pro hustotu energie magnetického pole platí:

  $$w=\frac{1}{2}\frac{B^2}{\mu_\mathrm{0}}.$$

  Odvození hustoty energie najdete v dalším oddíle.

  Hustotu energie dosadíme do rovnice (1) a dostáváme vztah:

  $$F\mathrm{d}x=\frac{1}{2}\frac{B^2}{\mu_\mathrm{0}}\mathrm{d}V.$$

  Infinitezimální objem dV při malém posunutí od jádra si můžeme vyjádřit jako dV = 2Sdx, kde S je průřez jádra. Protože jádro přisedá ke kotvě na dvou místech, musíme uvažovat dvě vzduchové mezery:

  $$F\mathrm{d}x=\frac{1}{2}\,\frac{B^2}{\mu_\mathrm{0}}\,2S\mathrm{d}x.$$

  Pro velikost síly, kterou musíme vykonat, aby se kotva odtrhla od ocelového jádra, dostáváme vztah:

  $$F=\frac{B^2}{\mu_\mathrm{0}}S.$$

  Za velikost magnetické indukce dosadíme výraz pro magnetickou indukci cívky a vezmeme v úvahu, že cívka je namotána na ocelovém jádře o relativní permeabilitě μ_r:

  $$B=\frac{\mu_\mathrm{0} \mu_\mathrm{r} N I}{l}.$$

  Síla potřebná na odtržení kotvy od jádra je tedy:

  $$F=\frac{\mu_\mathrm{0} {\mu_\mathrm{r}}^2 N^2 I^2S}{l^2}.$$

  Z výrazu pro velikost síly F vyjádříme neznámý proud I, který musí cívkou procházet:

  $$I=\frac{l}{\mu_\mathrm{r} N}\,{\sqrt{\frac{2F}{\mu_0 S}}}\mathrm{.}$$

• Odvození hustoty energie magnetického pole w

  Uvažujme cívku s průřezem o obsahu S. V ní sledujeme úsek délky l, který vymezuje uvnitř cívky objem V o velikosti Sl. Protéká-li cívkou proud I, vytvoří se uvnitř objemu V homogenní pole o velikosti magnetické indukce B. Pole vně cívky je téměř nulové.

  Pro celkovou energii magnetického pole cívky platí vztah:

  $$E=\frac{1}{2}LI^2.$$

  Hustotu energie pak můžeme vyjádřit jako:

  $$w=\frac{E}{V}=\frac{LI^2}{2Sl}.$$

  Za indukčnost L dosadíme vztah pro indukčnost cívky:

  $$L=\mu _0 N^2 lS.$$

  Pro hustotu magnetického pole tedy dostáváme výraz:

  $$w=\frac{1}{2}\frac{\mu_0 N^2lS I^2}{Sl}=\frac{1}{2}\mu_0 N^2 I^2.$$

  Uvědomíme-li si, že pro velikost magnetické indukce vně cívky platí tvar:

  $$B=\mu_\mathrm{0} N I,$$

  můžeme výraz pro hustotu energie upravit na tvar:

  $$w=\frac{1}{2}\frac{B^2}{\mu_\mathrm{0}}.$$

• Zápis a číselné dosazení

  $N = 600$	počet závitů cívky
  $\mu_\mathrm{r} = 1200$	relativní permeabilita oceli
  $S = 6{,}25\,\mathrm{cm^{2}}=6{,}25{\cdot} 10^{-4}\,\mathrm{m^{2}}$	průřez jádra cívky
  $l=50\,\mathrm{cm}=0{,}50\,\mathrm{m}$	délka střední siločáry
  $F=500\,\mathrm{N}$	síla držící kotvu
  $I = \mathrm{?}\,\mathrm{(A)}$	proud tekoucí cívkou
  Z tabulek:
  $\mu_\mathrm{0} = 4 \pi \cdot 10^{-7}\,\mathrm{H m^{-1} }$	permeabilita vakua

  ---

  $$I=\frac{l}{\mu_\mathrm{r} N}\,{\sqrt{\frac{F}{\mu_0 S}}}=\frac{0{,}5}{1200 {\cdot} 600}\,{\sqrt{\frac{500}{4\cdot \pi \cdot 10^{-7} \cdot 6{,}25{\cdot} 10^{-4}}}}\,\mathrm{A}\,\dot{=}\,0{,}554\,\mathrm{A} = 554\,\mathrm{mA}$$

• Odpověď

  Aby byla kotva k jádru držena silou 500 N, musí cívkou protékat proud o velikosti přibližně 554 mA.