Tvrdost oceli podle Brinella
Úloha číslo: 2147
Tvrdost oceli podle Brinella je 450. Jaký je průměr otisku, byla-li zkouška provedena kuličkou o průměru 5 mm při zatížení 2700 N?
Poznámka
Johan Augustus Brinell byl švédský inženýr, který přišel s metodou pro určení tvrdosti materiálu statickou zkouškou. Ta probíhá tak, že ocelová kulička působením síly proniká do zkoumaného materiálu. Důsledkem toho vzniká v materiálu otisk. Tvrdost pak můžeme určit pomocí poměru zatížení na kuličku a plochou vrchlíku otisku. Tvrdost je udána v kg·mm-2.
Zápis
HB = 4500 Nmm−2 tvrdost podle Brinella D = 5 mm průměr kuličky F = 2700 N zatížení při zkoušce d = ? mm průměr otisku Rozbor
Tvrdost oceli podle Brinella se bere jako podíl mezi silou, kterou kuličku tlačíme kolmo na povrch oceli, a plochou vrchlíku kuličky, která na povrchu oceli zůstane jako otisk. Budeme tedy potřebovat vyjádřit plochu vrchlíku ne v závislosti na jeho výšce, ale jeho průměru, a tedy i průměru otisku.
Nápověda
Připomeňte si vztah pro obsah vrchlíku. Využijte Thaletovu kružnici k vyjádření obsahu vrchlíku v závislosti na jeho průměru. Pak si napište vztah pro tvrdost a vyjádřete z něj hledaný průměr.
Řešení
Pro obsah vrchlíku platí vztah:
\[S\,=\,\pi Dv.\]Otisk kuličky si můžeme představit jako vrchlík koule. Proto bude dobré si zavést ještě výšku vrchlíku v a také a tak, aby platilo (viz obrázek):
\[D\,=\,2v+a.\tag{1}\]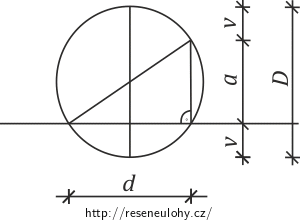
Když použijeme vlastnost Thaletovy kružnice, jak je tomu na obrázku, a Pythagorovu větu, pak můžeme a napsat ve tvaru:
\[a\,=\,\sqrt{D^2-d^2}.\tag{2}\]Ze (2) dosadíme do (1), pak:
\[D\,=\,2v+\sqrt{D^2-d^2}.\tag{3}\]Ze (3) vyjádříme v:
\[v\,=\,\frac{1}{2}\left({D-\sqrt{D^2-d^2}}\right).\tag{4}\]Pak už můžeme určit obsah vrchlíku:
\[S\,=\,\pi Dv\,=\,\frac{\pi D}{2}\left({D-\sqrt{D^2-d^2}}\right).\tag{5}\]Vztah pro tvrdost podle Brinella je:
\[H_\mathrm{B}\,=\,\frac{F}{S}\,=\,\frac{2F}{\pi D\left({D-\sqrt{D^2-d^2}}\right)}.\tag{6}\]Rovnici (6) můžeme upravit na:
\[D-\sqrt{D^2-d^2}\,=\,\frac{2F}{\pi D H_\mathrm{B}}.\tag{7}\]Dále ještě můžeme upravit na:
\[D^2-d^2\,=\,D^2-\frac{4F}{\pi H_\mathrm{B}}+\frac{4F^2}{\pi^2 D^2H_\mathrm{B}^2}.\tag{8}\]Nyní nám už zbývá pouze vyjádřit z (8) průměr otisku d:
\[d\,=\,\sqrt{\frac{4F}{\pi H_\mathrm{B}}-\frac{4F^2}{\pi^2 D^2H_\mathrm{B}^2}}.\tag{9}\]Můžeme už tedy dosadit a vypočítat:
\[d\,=\,\sqrt{\frac{4{\cdot}2700}{\pi \cdot4500}-\frac{4{\cdot}2700^2}{\pi^2 {\cdot}5^2{\cdot}4500^2}} \mathrm{mm}\,=\,0{,}871 \mathrm{mm}.\]Odpověď
Průměr otisku je:
\[d\,=\,0{,}871 \mathrm{mm}.\]

