Sinová věta (přímý důkaz)
Úloha číslo: 1929
Dokažte Sinovou větu:
Nechť ABC je obecný trojúhelník o délkách stran \(a,\,b,\,c\) a velikostech příslušných vnitřních úhlů \(\alpha,\,\beta,\,\gamma\), pak platí
\[\frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma}\,.\]Přímý a nepřímý důkaz
Přímý a nepřímý důkaz
Věty typu: „jestliže platí \(A\), pak platí \(B\)”, nebo-li \(A\Rightarrow B\) zpravidla dokazujeme pomocí přímého či pomocí nepřímého důkazu. Výrok \(A\) v tomto kontextu chápeme jako předpoklad tvrzení věty, výrok \(B\) pak jako závěr tvrzení věty.
V posloupnosti logicky správných kroků se snažíme dojít od pravdivého předpokladu k pravdivému závěru, v případě přímého důkazu. Alternativně se snažíme od neplatného závěru dojít v posloupnosti logicky správných kroků k neplatnosti předpokladu, v přápadě nepřímého důkazu.
Klíč k pochopení logiky přímého/nepřímého důkazu přitom spočívá v pravdivostní tabulce implikace.
Pravdivostní tabulka implikace
\[\begin{array}{|c|c|c|c|c|c|} A & B & A' & B'& A\Rightarrow B & B'\Rightarrow A'\\ \hline \color{red}{1}&\color{red}{1}&\color{red}{0}&\color{red}{0}&\color{red}{1}&\color{red}{1}\\ 1&0&0&1&0&0\\ 0&1&1&0&1&1\\ 0&0&1&1&1&1\\ \end{array}\]- Zvolíme-li cestu přímým důkazem, musíme z platnosti předpokladu \(A\) dojít přímo k platnosti implikace \(A\Rightarrow B\). V takovém případě totiž musí být nutně pravdivý i závěr \(B\) - viz červený řádek přiložené pravdivostní tabulky implikace.
- Zvolíme-li cestu nepřímým důkazem, musíme z neplatnosti negace závěru \(B'\) dojít přímo k platnosti obměněné implikace \(B'\Rightarrow A'\). V takovém případě totiž musí být nutně nepravdivá i negace předpokladu \(A'\) a platit tedy původní předpoklad \(A\) i závěr \(B\) - viz červený řádek přiložené pravdivostní tabulky implikace.
Poznamenejme na závěr, že komplikovanější věty, případně tvrzení, častokdy vyžadují pro svůj zdárný důkaz řetězec několika logicky správných implikací v duchu přímého či nepřímého způsobu dokazování výše.
Nápověda 1
Zhotovte si nejprve přehledný náčrt obecného (ne pravoúhlého atd.) trojúhelníku, zvýratněte v něm příslušné strany a úhly.
Nápověda 2
Zamyslete se, jak jste si zavedli skrze pravoúhlý trojúhelník funkci \(\sin \varphi\). Zároveň rozvažte, jak ve svém náčrtu vidět pro důkaz potřebné pravoúhlé trojúhelníky. Následně větu dokažte pomocí přímého důkazu.
Přímý důkaz?
Zbývá otázka, kde je v uvedeném sledu patrný způsob přímého dokazování? Z předpokladu jsme v posloupnosti logicky správných kroků došly přímo k pravdivému závěru.
- ABC je obecný trojúhelník.
- Výška je kolmá na příslušnou stranu.
- Definice funkce sinus v pravoúhlém trojúhelníku.
- Platnost Sinové věty.
Řešení
Trojúhelník si nepjrve načrtneme.
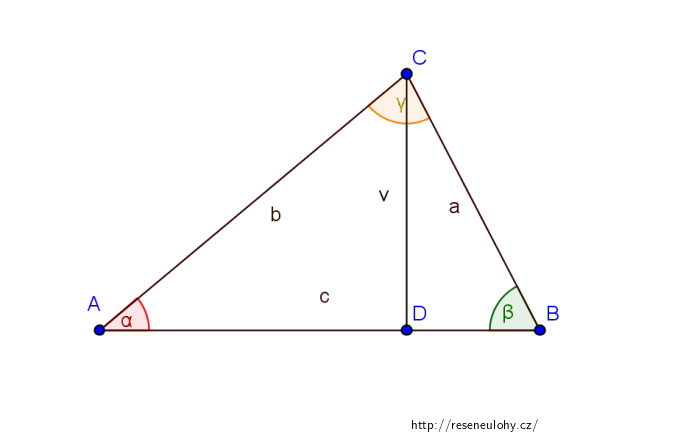
Spustíme-li dále například výšku \(v\) na stranu \(c\), získáme dva nové trojúhelníky.
Protože je výška určitě kolmá na příslušnou stranu, budou trojúhelníky ADC a DBC pravoúhlé s pravým úhlem při vrcholu D.
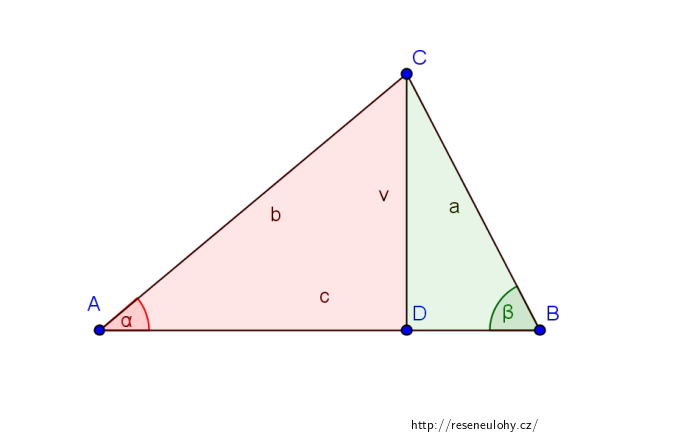
Využijeme-li nyní definice \(\sin\varphi=\)protilehlá ku přeponě, obdržíme v červeném trojúhelníku
\[\sin \alpha = \frac{v}{b} \Rightarrow v=b\sin\alpha\]a v zeleném trojúhelníku pak
\[\sin \beta = \frac{v}{a} \Rightarrow v=a\sin\beta\,.\]Porovnáme-li nyní obě rovnosti pro \(v\), konečně dojdeme ke kýženému
\[b\sin\alpha=a\sin\beta\Rightarrow \frac{a}{\sin\alpha}=\frac{b}{\sin\beta}\,.\]Pokud bychom celý postup zopakovali například pro dvojici pravoúhlých trojúhelníků získaných spuštěním výšky na stranu \(b\), snadno bychom tuto rovnost rozšířili na
\[\frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma}\,.\]Čímž můžeme Sinovou větu považovat za zdárně dokázanou!
Pravoúhlý/Tupoúhlý trojúhelník?
V případě pravoúhleho trojúhelníku bychom neměli co dokazovat, neboť by znění Sinové věty přešlo v definitorické vztahy pro Sinus jednotlivých úhlů v pravoúhlém trojúhelníku.
V případě tupoúhlého trojúhelníku bychom postupovali analogicky se zvoleným postupem pro trojúhelník ostroúhlý. Jednotlivé kroky by však byly méně názorné a myšlenkově průzračné.