Sbírka řešených úloh

Homogenní lineární rovnice s konstantními koeficienty - Matematické kyvadlo

Úloha číslo: 1869

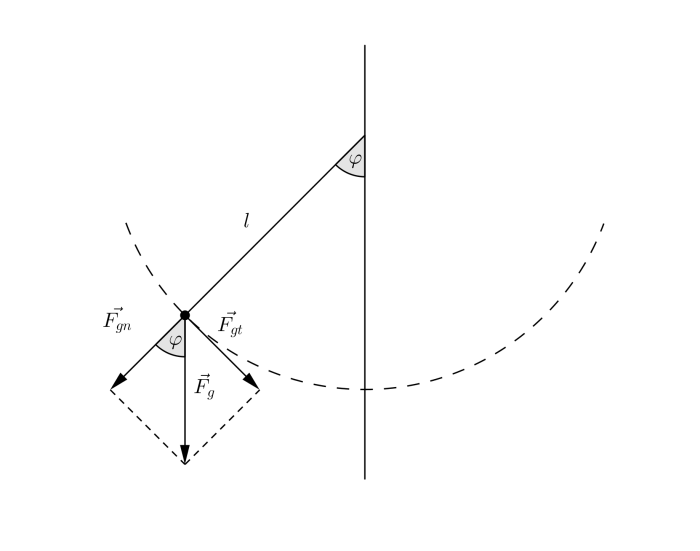
• Nákres, fyzikální rozbor situace a cesta k diferenciální rovnici

  Uvědomíme si, že směrem kolmo k zemi na kuličku působí gravitační síla \(F_g=mg\), kde \(g\) je gravitační konstanta. Její složku příslušející směru tečny ke kuličkou opisované kružnici tak můžeme vyjádřit jako \(F_{gt}= -mg\sin \varphi\), viz obrázek. Pro délku oblouku kružnice \(s\) odpovídající úhlu \(\varphi\) dále platí \(s=l\varphi\) a pro s tím spojenou časovou derivaci pak \(\ddot{s}=l\ddot{\varphi}\).

  

  Po následném využití druhého Newtonova zákona \(F=ma\) tak v rámci tečné složky získáme diferenciální rovnici

  \[m\ddot{s}=-mg\sin \varphi \,.\]

  S přihlédnutím k dříve uvedenému vztahu pro druhou derivaci \(\ddot{s}\) a skutečnosti, že pro malé úhly je \(\sin \varphi \cong \varphi\) tato rovnice nabude tvaru

  \[\ddot{\varphi}+\frac{g}{l} \varphi=0 \,.\]

  Jinými slovy, získáváme homogenní lineární diferenciální rovnici, kterou budume řešit v souladu s postupem z úlohy Homogenní lineární rovnice s konstantními koeficienty.

• Návrh řešení

  Pomocí znalostí osvojený v rozboru úlohy Homogenní lineární rovnice s konstantními koeficienty navrhněte obecnou podobu možného řešení rovnice.

• Návrh řešení

  Vzhledem ke skutečnosti, že se jedná o lineární homogenní rovnici s konstantními koeficienty, budeme její řešení hledat ve tvaru

  \[ y=\mathrm{e}^{\lambda x} \,.\]

• Charakteristická rovnice

  Pomocí navrhovaného řešení určete charakteristickou rovnici.

• Charakteristická rovnice

  Po dosazení navrhovaného řešení do řešené rovnice obdržíme charakteristickou rovnici

  \[\begin{align*} \lambda^2+\frac{g}{l} &=0 \\ \lambda^2 &=-\frac{g}{l} \\ \lambda &= \pm i \sqrt{\frac{g}{l}}\,. \end{align*}\] .

• Obecné řešení

  Pomocí kořenů charakteristické rovnice určete podobu obecného řešení řešené homogenní rovnice.

• Obecné řešení

  Protože jsme obdrželi jednonásobnou dvojici komplexně sdružených kořenů, vyjádříme příslušná řešení jako \(\cos \sqrt{\frac{g}{l}} t\), \(\sin \sqrt{\frac{g}{l}} t\) a hledané obecné řešení pak ve tvaru

  \[\varphi_h(t)=c_1\cos \sqrt{\frac{g}{l}} t + c_2\sin \sqrt{\frac{g}{l}} t \,.\]

• Řešení

  Vzhledem ke skutečnosti, že se jedná o lineární homogenní rovnici s konstantními koeficienty, budeme její řešení hledat ve tvaru

  \[ y=\mathrm{e}^{\lambda x} \,.\]

  Po dosazení navrhovaného řešení do řešené rovnice obdržíme charakteristickou rovnici

  \[\begin{align*} \lambda^2+\frac{g}{l} &=0 \\ \lambda^2 &=-\frac{g}{l} \\ \lambda &= \pm i \sqrt{\frac{g}{l}}\,. \end{align*}\] .

  Protože jsme obdrželi jednonásobnou dvojici komplexně sdružených kořenů, vyjádříme příslušná řešení jako \(\cos \sqrt{\frac{g}{l}} t\), \(\sin \sqrt{\frac{g}{l}} t\) a hledané obecné řešení pak ve tvaru

  \[\varphi_h(t)=c_1\cos \sqrt{\frac{g}{l}} t + c_2\sin \sqrt{\frac{g}{l}} t \,.\]