Přímá integrace II. (Volný pád)
Úloha číslo: 1717
Motivace
Rovnice typu \(y'=f(x)\), přímá integrace
Za předpokladu, že lze pravou stranu rovnice integrovat na intervalu \(I\) (čímž budeme nadále v tomto kontextu rozumět, že k dané funkci lze na \(I\) nalézt příslušnou primitivní funkci), získáme hledané obecné řešení přímou integrací
\[y(x)=\int{f(x)}\mathrm{d}x \,.\]Obdržíme tak
\[y(x)=F(x)+C\,,\]kde \(C\) je integrační konstanta a \(F(x)\) primitivní funkce k \(f(x)\) na \(I\). Řešení celé diferenciální rovnice tak přechází v hledání primitivní funkce.
Znázornění situace a pohybová rovnice
Nejprve se zaměřte na zmatematizování fyzikálního problému. Situaci graficky znázorněte, proveďte rozbor sil a následně sestavte příslušnou pohybovou rovnici.
Vydobytí diferenciální rovnice
Pomocí definice zrychlení ze získané pohybové rovnice vydobyjte kýženou rovnici diferenciální, jejíž řešení povede k hledané funkci \(v(t)\).
Řešení získané diferenciální rovnice
V souladu s motivačním úvodem úlohy nyní pomocí přímé integrace nalezněte hledané řešení získané diferenciální rovnice.
Vydobytí druhé diferenciální rovnice
Skrze definici rychlosti vydobuďte diferenciální rovnici vedoucí k hledané funkci \(x(t)\).
Řešení druhé získané diferenciální rovnice
V souladu s motivačním úvodem úlohy nyní pomocí přímé integrace nalezněte hledané partikulární řešení druhé získané diferenciální rovnice.
Řešení
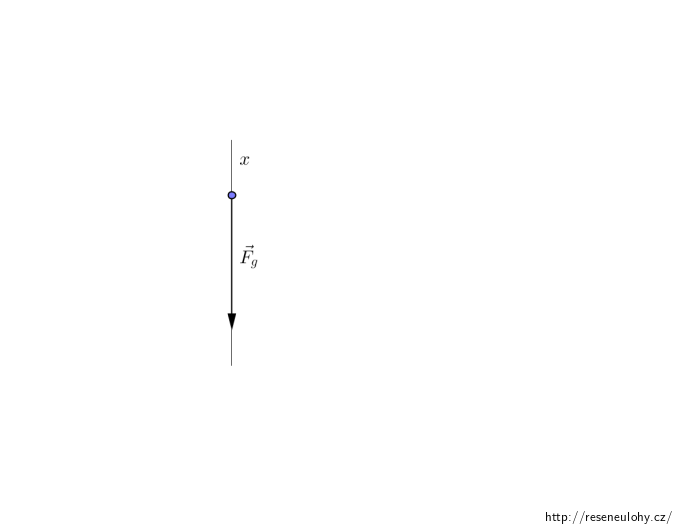
Protože se těleso pohybuje po přímce kolmé k povrchu Země, vystačíme si s jednodimenzionálním přiblížením, kdy na těleso působí pouze tíhová síla \(F_{g}=-mg\) proti směru osy \(x\) a \(x\)-ová souřadnice značí aktuální výšku tělesa nad povrchem, viz obrázek 2.1.
Z druhého Newtonova zákona \( F=ma \), volně přeloženého jako: když zrychlení, tak síla}, získáváme pohybovou rovnici
\[ma=-mg\,.\]Obě strany získané pohybové rovnice krátíme \(m\). Dále využijeme skutečnosti, že zrychlení udává změnu rychlosti za čas. Což v řeči derivací znamená \(a=\dot{v}\). Celou rovnici tak přepíšeme následujícím způsobem
\[\dot{v}=-g \,,\]čímž obdržíme obyčejnou diferenciální rovnice ve tvaru \( y'(x)=f(x) \). Uvědomíme si, že konstantní funkce \(f(x)=g\) je spojitá na \(\mathbb{R}\). Získanou diferenciální rovnici proto můžeme řešit přímou integrací.
Poznámka: Tečka, dle Newtonovy notace, ve fyzice značí derivaci podle času. Toto značení Newton zavedl ve svých Principiích v rámci zjednodušení matematického zápisu. Fyziky totiž nejčastěji zajímají právě změny veličin s časem.
Přímou integrací tak získáváme
\[v=-\int{g} \,\mathrm{d}t = -gt + C \,,\]kde \(C\) je integrační konstanta, jejíž přesnou hodnotu určíme z počáteční podmínky \( v(0)=0\). Ve vztahu pro \( v \) proto položíme \( t = 0 \) , nebo-li
\[0=-0+C \Rightarrow C=0 \,.\]Celkově tak získáme partikulární řešení ve tvaru
\[v(t)= -gt\,.\]Zbývá určit funkci \( x(t) \), popisující polohu tělesa v čase \(t\). I v tomto případě si uvědomíme, že rychlost vyjadřuje změnu polohy za čas. Což v řeči derivací znamená \( v=\dot{x}\). Vztah pro \(v(t)\) tak přepíšeme následujícím způsobem
\[\dot{x}= -gt\,.\]Opět před sebou máme obyčejnou diferenciální rovnici ve tvaru \(y'(x)=f(x) \). Lineární funkce \( f(x)=gt \) je spojitá na \( \mathbb{R} \). Získanou diferenciální rovnici proto můžeme opět řešit přímou integrací.
\[x= \int {-gt}\,\mathrm{d} t = -\frac{1}{2}gt^2 + C \,,\]což je obecné řešení této diferenciální rovnice na \(\mathbb{R}\) kde \(C\) je integrační konstanta. Dále využijeme počáteční podmínky \( x(0)=h_0 \). Po dosazení
\[h_0= 0 + C \Rightarrow C = h_0\]tak konečně získáme hledané partikulární řešení ve tvaru
\[ x(t)=-\frac{1}{2}gt^2 + h_0 \,.\]