Úloha o řetězovce (snižování řádu)
Úloha číslo: 1892
Určete parametrizaci řetězovky, tj. křivky, jež má tvar řetězu (homogenního ohebného vlákna) zavěšeného ve dvou různých stejně vysokých bodech.
Naším úkolem je, jinými slovy, nalézt funkci, jejímž grafem je řetězovka. Pro zjednodušení položíme soustavu souřadnou tak, aby minimum této funkce (vrchol řetězovky), leželo na ose \(y\), tj \(y'(0)=0\). Ze symetrie zavěšení je dále patrné, že hledáme sudou funkci.
Tento příklad je volně převzat z přednášky Doc. RNDr. Antonína Slavíka, Ph.D., Diferenciální geometrie I.
Fyzikální rozbor a cesta k diferenciální rovnici
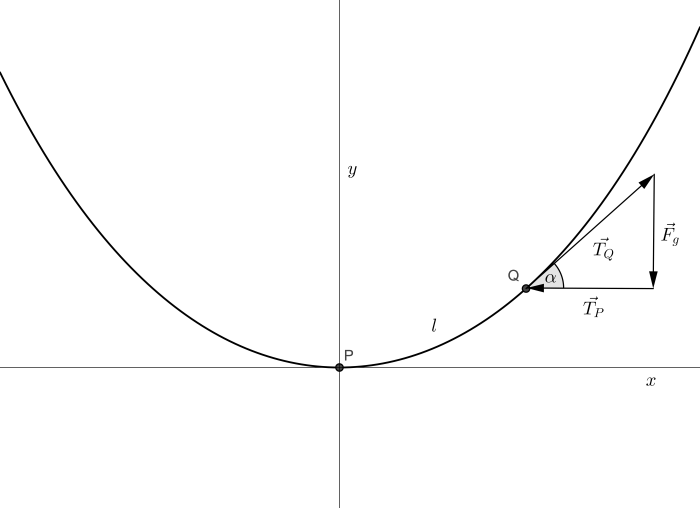
Na řetězovce zvolíme bod \(Q=\bigl[x, y(x)\bigr]\) a uvědomíme si, že velikost tíhové síly působící na část řetězu mezi počátkem \(P\) a bodem \(Q\) je přímo úměrná hmotnosti této části, a ta zase přímo úměrná její délce. Nebo-li
\[F_g \sim m \sim l \,,\]kdy délku \(l\) můžeme vyjádřit pomocí známého vztahu
\[l=\int\limits_{0}^{x} \sqrt{1+{y'(t)}^2}\mathrm{d}t \,.\]Provedeme-li dále rozbor sil působících na pozorovaný segment řetězu mezi body \(P\), \(Q\), vypozorujeme, že v bodě \(Q\) působí síla pnutí \(T_Q\) ve směru tečny směrem od bodu \(P\), v bodě \(P\) pak na opačnou stranu taktéž ve směru tečny síla pnutí \(T_P\) a v těžišti segmentu, tj. uprostřed, konečně ve směru osy \(y\) směrem k zemi tíhová síla \(F_g\), viz obrázek. Protože je řetěz ve statické poloze, tj. v rovnováze, účinky těchto sil se musejí nutně vzájemně rušit. Nebo-li
\[\vec{F_g}+\vec{T_P}+\vec{T_Q} = 0 \,.\]Přesuneme-li všechny síly do bodu \(Q\), viz obrázek, vidíme, že pro tangens úhlu \(\alpha\) platí
\[\mathrm{tg}\, \alpha = \frac{F_g}{T_P} \,.\]Vzpomeneme si dále, že derivace \(y'\) v bodě \(x\) odpovídá směrnici tečny v tomto bodě a dojdeme ke vztahu
\[y'(x)=\mathrm{tg}\, \alpha \Rightarrow y'(x)=\frac{F_g}{T_P} \,.\]Protože je ale \(F_g\) působící na segment přímo úměrná jeho délce, je této délce díky předchozímu závěru přímo úměrná i derivace \(y'(x)\). Jinými slovy
\[ y'(x)=\frac{1}{c}\int\limits_{0}^{x} \sqrt{1+{y'(t)}^2}\mathrm{d} t\,.\]Derivujeme-li následně získanou rovnici dle proměnné \(x\), obdržíme diferenciální rovnici druhého řádu
\[y''=\frac{1}{c} \sqrt{1+{y'(x)}^2}\,.\]Snížení řádu
V souladu s Úloha o řetězovce (snižování řádu) nejprve snižte řád řešené rovnice zavedením vhodné substituce.
Přímá integrace
Pomocí přímé integrace vyřešte substitucí získanou rovnici.
Řešení
Než začneme tuto rovnici řešit, nejprve snížíme její řád zavedením substituce \(w(x)=y'(x)\). Přejdeme tak k rovnici se separovanými proměnnými
\[\begin{align*} w'&=\frac{1}{c} \sqrt{1+{w}^2} \\ \frac{w'}{\sqrt{1+{w}^2}}&=\frac{1}{c} \,. \end{align*}\]Tuto rovnici dále integrujeme
\[\int\frac{\mathrm{d} w}{\sqrt{1+{w}^2}}=\frac{1}{c}\int 1 \mathrm{d} x \,. \]Integrál na levé straně řešíme zavedením hyperbolické substituce \(w=\sinh v\), kde \(\mathrm{d} w=\cosh v \mathrm{d} v\) , získáme tak
\[\int\frac{\cosh v \mathrm{d} v}{\sqrt{1+{\sinh v}^2}}=\frac{1}{c}\int 1 \mathrm{d} x \,.\]S využitím vztahu \(1+\sinh v^2 = \cosh v ^2\) pak
\[\int 1 \mathrm{d} v=\frac{1}{c}\int 1\mathrm{d} x \,. \]Po nalezení příslušných primitivních funkcí následně
\[v=\frac{1}{c}x + k \,,\]a po zpětné substituci konečně
\[\operatorname{arcsinh}\,w=\frac{1}{c}x + k \Rightarrow w=\sinh\left(\frac{1}{c}x + k\right)\,.\]Vzpomeneme si na námi zavedenou počáteční podmínku \(y'(0) = 0\), tedy \(w(0)=0\) a určíme konstantu \(k\) jako
\[0=\sinh(0 + k)\Rightarrow k =0 \,.\]K hledané funkci \(y(x)\) nakonec přejdeme pomocí prvního užitého substitučního vztahu \(y'(x)=w(x)\), nebo-li
\[\begin{align*} y'&=\int \sinh \left(\frac{x}{c}\right) \mathrm{d} x \\ y(x)&=c \cosh \left(\frac{x}{c}\right) + L \,, \end{align*}\]kde konstanta \(L\) určuje posunutí. Celkově tak můžeme říci, že řetězovka je grafem funkce \(\cosh (x)\).