Vyšetřete průběh funkce - jednoduchá kubická funkce úvodem

Tato úloha neprošla kontrolou správnosti.

Vyšetřete průběh funkce - jednoduchá kubická funkce úvodem

Úloha číslo: 1259

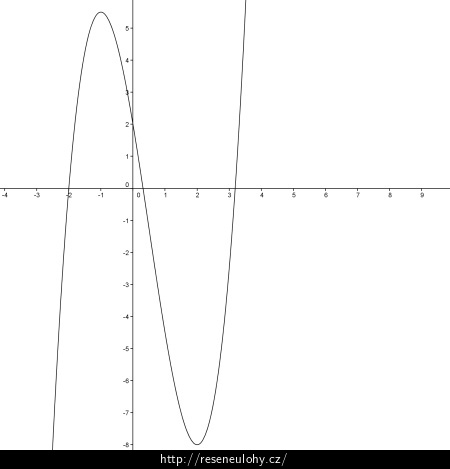
Vyšetřete průběh funkce:

\[f(x)=x^3-\frac{3}{2}x^2-6x+2\]

Rozbor
Co si přesně představit pod úlohami typu vyšetřete průběh funkce?

Naším úkolem bude získat co nejvíce vlastností funkce, abychom měli co nepřesnější představu o jejím průběhu a abychom byli schopni nakreslit co možná nejpřesnější graf zadané funkce.

Zejména nás budou zajímat tyto vlastnosti(zachována logická posloupnost vyšetřovaných vlastností):
1. Určete definiční obor funkce a případné body nespojitosti.
2. Ověřte, zdali je funkce sudá, lichá nebo periodická. V kladném případě můžeme další úkony omezit na nekladnou/nezápornou část osy nebo v případě, že je funkce periodická na interval jedné periody.
3. Spočtěte jednostranné limity v hraničních bodech definičního oboru funkce a v případných bodech nespojitosti. Získáte tak představu o případné omezenosti/neomezenosti funkce.
4. Pomocí záskané první derivace určete intervaly růstu a klesání funkce a její lokální maxima/minima
  
  Pokud to jde, určete jednostranné limity derivace zleva a zprava v těch bodech definičního oboru, kde první derivace neexistuje (určují sklon grafu funkce v těchto bodech)
5. Určete druhou derivaci funkce a s tím spojené body podezřelé z inflexe.
6. Pomocí záskané druhé derivace určete intervaly konvexnosti/konkávnosti funkce a její inflexní body
7. Ověřte, zdali funkce nemá asymptoty(tečny v nekonečnu)
8. Vypočítejte hodnoty, jichž funkce nabývá v důležitcý bodech - tj. v průsečících s osami, v bodech nespojitosti, v bodech extrémů funkce a v inflexních bodech.
9. Za pomoci získaných informací sestrojte graf funkce
Nápověda 1. - definiční obor a body nespojitosti.
Představte si, jak zkoumaná funkce vypadá (pro představu vzpomeňte na \(g(x)=x^3\)) a pro jaké hodnoty x je definována, případně, pro které hodnoty nemá smysl.
Nápověda 1. - řešení - definiční obor a body nespojitosti.
Funkce \(f(x)=f(x)=x^3-\frac{3}{2}x^2-6x+2\) má evidentně smysl pro všechna reálná čísla, neboť je složena z funkcí, jež jsou definovány pro všechna reálná čísla. O definičním oboru tedy můžeme prohlásit, že:
\[D_f=R\]
Nápověda 2. - Periodičnost, Sudost a Lichost.
Zamyslete se nad tím, jaké funkce obvykle bývají periodicé, jestli může být tedy i zadaná funkce periodická, případně určete periodu.

K vyšetření symetrie funkce je potřeba znát podobu grafu předem nebo vycházet z definice sudé/liché, případně periodické funkce.
Nápověda 2.- Řešení - Periodičnost, Sudost a Lichost.
Periodické obvykle bývají funkce goniometrické či cyklometrické, jak je známo, tak obecně mocniná funkce periodická není.

Můžeme také vyjít přímo z definice periodické funkce:
\[f(x+t)=f(x);\,\,t\ne 0\]
kde t rozumíme periodou funkce.

Pro jistotu ještě ověříme náš závěr výpočtem:
\[f(x+t)=(x+t)^3-\frac{3}{2}(x+t)^2-6(x+t)+2\overset{\underset{\mathrm{?}}{}}{=}x^3-\frac{3}{2}x^2-6x+2=f(x)\]
Je patrné na pvní pohled, že rovnost platí pouze pro hodnotu parametru \(t=0\) a zkoumaná funkce tedy skutečně není periodická(můžeme ověřir a dopočíst).

Sudost či lichost vyšetříme pomocí definice těchto dvou vlastností funkce, kdy platí:
\[f(-x)=-f(x)\]
pro funkci lichou
\[f(-x)=f(x)\]
pro funkci sudou

Po dosazení získáváme rovnost:
\[f(-x)=(-x)^3-\frac{3}{2}(-x)^2-6(-x)+2=-x^3-\frac{3}{2}x^2-6x+2\]
Což je různé jak od \(f(x)\)(můžeme snadno ověřit porovnáním), tak i od \(-f(x)\), z čehož plyne, že vyšetřovaná funkce není sudá ani lichá.

K tomuto poznání jsme ovšem mohli dojít bez jakéhokoli výpočtu, neboť je patrné, že je graf funkce posunutý na ose x, z čehož plyne, že funkce nemůže být symetrická vzhledem k ní ani k bodu [0,0].
Nápověda 2.- jednostranné limity v hraničních bodech a bodech nespojitosti
S využitím definice jednostranných limit a vět pro počítání limit funkcí spočteme limity v hraničních bodech D_f, což jsou v našem případě hodnoty plus a minus nekonečno.
Nápověda 2.- Řešení - jednostranné limity v hraničních bodech a bodech nespojitosti
Víme, že hraničními body D_f jsou hodnoty \(-\infty\) a \(+\infty\).

Hledanou limitu v \(+\infty\) vypočteme, dle definice jednostranné limity, jako:
\[\lim_{x \to +\infty_{-}}{x^3-\frac{3}{2}x^2-6x+2}=\lim_{x \to +\infty_{-}}{x^3(1-\frac{3}{2x}-\frac{6}{x^2}+\frac{2}{x^3})}\] \[=+\infty\cdot(1-0-0+0)=+\infty\]
Hledanou limitu v \(-\infty\) vypočteme analogycky, dle definice jednostranné limity, jako:
\[\lim_{x \to -\infty_{+}}{x^3-\frac{3}{2}x^2-6x+2}=\lim_{x \to -\infty_{+}}{x^3(1-\frac{3}{2x}-\frac{6}{x^2}+\frac{2}{x^3})}\] \[=-\infty\cdot(1-0-0+0)=-\infty\]
Díky spočteným limitám jsme již nyní schopni prohlásit, že je funkce neomezená shora i zdola(nabývá hodnot od minus do plus nekonečna).
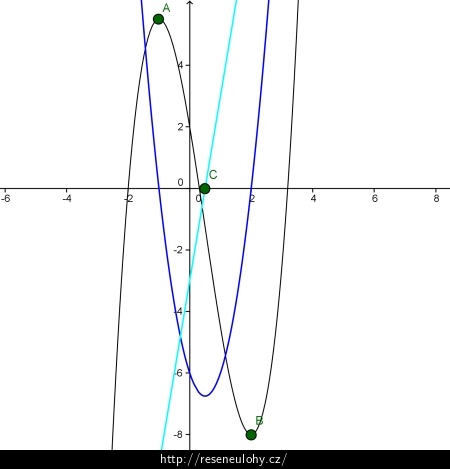
Nápověda 3.- První derivace a body podezřelé z extrémů
Pomocí známých derivací Základní derivace funkcí jedné reálné proměnné nebo přímo z definice derivace vypočteme její hodnotu pro zkoumanou funkci. Následně za pomoci nutné podmínky existence lokálního extrému určíme body podezřelé z extrémů.
Nápověda 3.- Řešení - První derivace a body podezřelé z extrémů
Například pomocí známé derivace obecné mocninné funkce z úlpohy Základní derivace funkcí jedné reálné proměnné vypočítáme derivace zkoumané funkce jako:
\[f^{\prime}(x)=(x^3-\frac{3}{2}x^2-6x+2)^{\prime}=3x^2-3x-6\]
Nutnou podmínkou pro existenci lokálního extrému je, že pokud má funkce v daném bodě vlastní první derivaci, její hodnota je rovna 0. Hledáme tedy takové body/taková x, v nichž první derivace nabývá nulové hodnoty nebo v nichž neexistuje.

Polynom upravíme tak, abychom byli schopni určit kořeny:
\[f^{\prime}(x)=3x^2-3x-6=3(x+1)(x-2)\]
Je tedy patrné, že body, v nichž je funkce podezřelá z nabývání extrémů jsou \(x=-1\) a \(x=2\), neboť:
\[f^{\prime}(-1)=3(-1+1)(-1-2)=3{\cdot} 0\cdot (-3)=0\] \[f^{\prime}(2)=3(2+1)(2-2)=3{\cdot}3\cdot 0=0\]
Nápověda 4.- Intervaly růstu a klesání, lokální extrémy
Pomocí již známé první derivace a vlastnosti roztu/klesání funkce ve spojitosti právě s její první derivací určete intervaly růstu a klesání, jakmile tyto intervaly budou určeny, budete schopni rozhodnout z definice lokálního extrému, zdali jsou námi zjištěné body podezřelé z extrémů skutečně extrémy funkce či nikoli.
Nápověda 4.- Řešení - Intervaly růstu a klesání, lokální extrémy
Vzhledem ke skutečnosti, že body podezřelé z extrému jsou \(2\) a \(-1\), zkoumané intervaly budou tedy vypadat \((-\infty ,-1)\), \((-1 ,2)\) a \((2,+\infty)\) a následně ověříme, jakých hodnot na něm funkce nabývá(což provedeme metodou dosazení vnitřního bodu intervalu).

Je patrné, že pro \(x \in(-\infty,-1)\) první derivace \(f^{\prime}(x)=3(x+1)(x-2)\) nabývá kladných hodnot, z věty o první derivace a monotonii funkce plyne, že na tomto intervalu je zkoumaná funkce roztoucí.

Dále opět dosazením zjišťujeme, že pro \(x \in(-1{,}2)\) první derivace \(f^{\prime}(x)=3(x+1)(x-2)\) nabývá záporných hodnot, z věty o první derivace a monotonii funkce plyne, že na tomto intervalu je zkoumaná funkce klesající.

Nakonec tradičním dosazením zjišťujeme, že pro \(x \in(2,+\infty)\) první derivace \(f^{\prime}(x)=3(x+1)(x-2)\) nabývá kladných hodnot, z věty o první derivace a monotonii funkce plyne, že na tomto intervalu je zkoumaná funkce roztoucí.

Nyní víme, že existuje pravé okolí bodu -1, v němž je zkoumaná funkce klesající a levé okolé bodu -1, v němž je zkoumaná funkce roztoucí, z čehož a z definice lokálního minima plyne, že má zkoumaná funkce v bodě -1 lokální maximum.

Nyní víme, že existuje pravé okolí bodu 2, v němž je zkoumaná funkce roztoucí a levé okolé bodu 2, v němž je zkoumaná funkce klesající, z čehož a z definice lokálního minima plyne, že má zkoumaná funkce v bodě 2 lokální minimum.
Nápověda 5.- druhá derivace a body podezřelé z inflexe.
Pomocí známých derivací nebo přímo z definice derivace vypočteme její hodnotu pro zkoumanou funkci ze znalosti derivace první. Následně za pomoci nutné podmínky existence inflexe určíme body podezřelé z inflexe.
Nápověda 5.- Řešení- druhá derivace a body podezřelé z inflexe.
Například pomocí známé derivace obecné mocninné funkce z úlpohy Základní derivace funkcí jedné reálné proměnné vypočítáme derivace zkoumané funkce jako:
\[f^{''}(x)=\left(x^3+\frac{3}{2}x^2+6x+2)^{''}=(3x^2-3x+6 \right)^{\prime}=6x-3=3(2x-1)\]
Nutnou podmínkou pro existenci inflexnho bodu je, že existuje-li druhá derivace v tomto bodě, pak je její hodnota 0, hledáme tedy takové body/taková x, v nichž druhá derivace nabývá nulové hodnoty nebo body, v nichž neexistuje.

Na první pohled je patrné, že takovým bodem je hodnota \(\frac{1}{2}\) a tento bod je tedy podezřelý z inflexe.
Nápověda 6. - konvexita/konkávnost zkoumané funkce a inflexní body
Pomocí již známé druhé derivace a vlastnosti konvexity/konkávnosti funkce ve spojitosti právě s druhou derivací určete intervaly konvexity/konkávnosti, jakmile tyto intervaly budou určeny, budete schopni rozhodnout z definice inflexního bodu, zdali jsou námi zjištěné body podezřelé z inflexe skutečně inflexními body funkce či nikoli.
Nápověda 6. - Řešení - konvexita/konkávnost zkoumané funkce a inflexní body
Vzhledem ke skutečnosti, že bod podezřelý z inflexe je \(\frac{1}{2}\), zkoumané intervaly budou tedy vypadat \((-\infty ,\frac{1}{2})\) a \((\frac{1}{2} ,+\infty)\). Ověříme tedy, jakých hodnot na něm funkce nabývá(což provedeme metodou dosazení vnitřního bodu intervalu).

Je patrné, že pro \(x \in (-\infty ,\frac{1}{2})\) druhá derivace \(f^{''}(x)=3(2x-1)\) nabývá záporných hodnot, z věty o druhé derivace a konvexitě/konkávnosti funkce plyne, že na tomto intervalu je zkoumaná funkce konkávní.

Dále je patrné, že pro \(x \in (\frac{1}{2} ,+\infty)\) druhá derivace \(f^{''}(x)=3(2x-1)\) nabývá kladných hodnot, z věty o druhé derivace a konvexitě/konkávnosti funkce plyne, že na tomto intervalu je zkoumaná funkce konvexní.

Nyní víme, že existuje pravé okolí bodu \(\frac{1}{2}\), v němž je zkoumaná funkce konvexní a levé okolé bodu \(\frac{1}{2}\), v němž je zkoumaná funkce konkávní, z čehož a z definice inflexního bodu plyne, že má zkoumaná funkce v bodě \(\frac{1}{2}\) inflexi.
Nápověda 7.- Asymptoty
Z definice asymptoty a věty pro její určení určete rovnice obou těchto přímek.
Nápověda 7.- Řešení - Asymptoty
Víme, že pokud má funkce asymptoty, pak koeficienty a, b rovnice této přímky \(y=ax+b\) získáme jako(přičemž a, b jsou konečná reálná čísla):
\[a=\lim_{x \to +\infty}\frac{f(x)}{x}\] \[b=\lim_{x \to +\infty}f(x)-ax\]
pro asymptotu v plus nekonečnu
\[a=\lim_{x \to -\infty}\frac{f(x)}{x}\] \[b=\lim_{x \to -\infty}f(x)-ax\]
pro asymptotu v minus nekonečnu

Nejprve určíme asymptotu v plus nekonečnu:

Pro koeficient a tedy po dosazení do limity získáváme:
\[a=\lim_{x \to +\infty}\frac{x^3+\frac{3}{2}x^2+6x+2}{x}=\lim_{x \to +\infty}x^2+\frac{3}{2}x+6+\frac{2}{x}=\] \[=\lim_{x \to +\infty}x^2\left(1-\frac{3}{2x}-\frac{6}{x^2}+\frac{2}{x^3}\right)=+\infty(1-0-0+0)=+\infty\]
protože koeficient a není konečné reální číslo, z toho plyne, že v plus nekonečnu tato funkce asymptotu nemá.

Poté určíme asymptotu v minus nekonečnu:

Pro koeficient a tedy po dosazení do limity získáváme:
\[a=\lim_{x \to -\infty}\frac{x^3+\frac{3}{2}x^2+6x+2}{x}=\lim_{x \to -\infty}x^2+\frac{3}{2}x+6+\frac{2}{x}=\] \[=\lim_{x \to -\infty}x^2\left(1-\frac{3}{2x}-\frac{6}{x^2}+\frac{2}{x^3}\right)=+\infty(1-0-0+0)=+\infty\]
protože koeficient a není konečné reální číslo, z toho plyne, že v minus nekonečnu tato funkce asymptotu nemá.

Pozorováním jsme však k tomuto zjištění mohli dojít daleko snáze, neboť je funkce neomezená, z čehož plyne, že nemůže mít asymptoty.
Nápověda 8.- Dopočtení důležitých hodnot
Vypočítejte, jakých hodnot zkoumaná funkce nabývá ve svých případných průsečících s osami, extrémech, bodech nespojitosti a inflexních bodech
Nápověda 8.- Řešení - Dopočtení důležitých hodnot
Nyní prostým dosazením do \(f(x)=f(x)=x^3-\frac{3}{2}x^2-6x+2\) dopočteme zmíněné, pro graf podstatné, hodnoty.

Průsečík s osou y tak, že za x dosadíme 0:
\[f(0)=f(x)=0^3-\frac{3}{2}0^2-6(0)+2=2\]
Průsečíkem s osou y tedy bude bod [0,2]

Průsečíky z osou x zjistíme tak, že 0 dosadíme za y:
\[0=f(x)=x^3-\frac{3}{2}x^2-6x+2\]
z čehož plyne, že těmito průsečíky jsou body [0,-2],\([0,\frac{1}{4}(7-\sqrt{33})]\) a \([0,\frac{1}{4}(7+\sqrt{33})]\)

Body nespojitosti nebyly zjištěny.

Funkce nabývá extrému a to v -1 a 2, kde hodnota funkce v těchto bodech je:
\[f(-1)=(-1)^3-\frac{3}{2}(-1)^2-6(-1)+2=5{,}5\] \[f(2)=(2)^3-\frac{3}{2}(2)^2-6(2)+2=-8\]
Zkoumaná funkce má inflexní bod v \(\frac{1}{2}\), kde nabývá hodnoty:
\[f\left(\frac{1}{2}\right)=\left(\frac{1}{2}\right)^3-\frac{3}{2}\left(\frac{1}{2}\right)^2-6\left(\frac{1}{2}\right)+2=-\frac{5}{4}\]
Nápověda 9. - Graf
Ze získaných údajů sestrojte co nejpřesnější graf zkoumané funkce.
Nápověda 10.- Řešení - Graf
Graf - doplňující materiál pro kontrolu

Tmavě modře je znázorněna derivace první, světle modře pak derivace druhá, body A a B(bod A maximum a bod B minimum) jsou lokálními extrémy a bod C inflexním bodem.