Sbírka řešených úloh

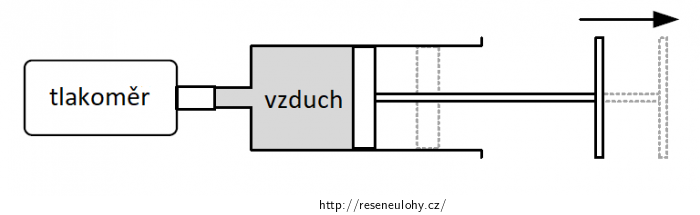
Stav vzduchu ve stříkačce (děje s ideálním plynem)

Úloha číslo: 4508

V injekční stříkačce je vzduch s objemem 10,0 cm³ při normálním tlaku vzduchu 100 kPa a teplotě 20 °C, která je stejná jako teplota okolí.

Na injekční stříkačku umístíme tlakoměr. Objem vzduchu ve stříkačce zvyšujeme pomalým pohybem pístu. Předpokládejte, že teplota vzduchu ve stříkačce je během této změny konstantní a rovná se teplotě okolí.

a)	Vypočítejte hmotnost vzduchu v injekční stříkačce. Hmotnost kilomolu vzduchu je 29 kg.
b)	Objem vzduchu ve stříkačce se izotermicky zvětší na 12,5 cm3. Vypočítejte jeho tlak. Zapište změnu vnitřní energie vzduchu ve stříkačce.
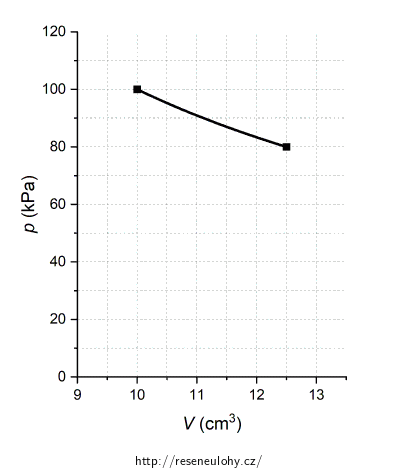
c)	Do pV diagramu nakreslete popsanou izotermickou změnu stavu vzduchu v injekční stříkačce.
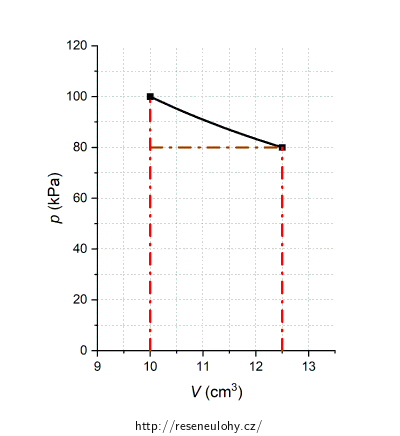
d)	Vypočítejte obsah plochy pod grafem, který jste načrtli v zadání c) této úlohy. Pojmenujte fyzikální veličinu reprezentovanou touto plochou. Křivku při výpočtu obsahu plochy aproximujte úsečkou.
e)	Vypočítejte teplo, které si vzduch ve stříkačce vymění s okolím při změně popsané v bodě b).
f)	Stěny injekční stříkačky izolujeme a experiment opakujeme. V tomto případě si vzduch nevymění teplo s okolím. Když se objem vzduchu ve stříkačce zvýší z 10,0 cm3 na 12,5 cm3, změní se jeho teplota. Napište, jestli je po této změně stavu vzduchu ve stříkačce jeho hustota, tlak a vnitřní energie vyšší, nižší nebo stejná v porovnání se stavem po první změně (zadání b) této úlohy). Svoji odpověď zdůvodněte.

• Zápis

  V1 = 10,0 cm3 = 10-5 m3	objem vzduchu ve stříkačce
  p1 = 100 kPa = 107 Pa	tlak vzduchu ve stříkačce
  T = 293,15 K	teplota vzduchu ve stříkačce v K

  ---

  a) Mm = 29 kg	hmotnost kilomolu vzduchu
  m = ?	hmotnost vzduchu ve stříkačce
  b) V2 = 12,5 cm3 = 1,25·10-5 m3	objem vzduchu po izotermickém zvětšení
  p2 = ?	tlak po izotermickém zvětšení
  \(\Delta U\) = ?	změna vnitřní energie během expanze
  d) S = ?	Obsah plochy pod grafem v c)
  e) Q = ?	teplo, které si vzduch vymění s okolím

• Nápověda a) Hmotnost vzduchu

  Vzduch ve stříkačce budeme považovat za ideální plyn. Známe jeho tlak, objem a teplotu. Vzpomeňte si, jaká rovnice tyto tři stavové veličiny spojuje. S její pomocí vyjádřete hmotnost vzduchu ve stříkačce.

• Řešení nápovědy a) Hmotnost vzduchu

  Vyjdeme ze stavové rovnice ideálního plynu, ve tvaru: \[pV = nRT,\] kde n je látkové množství. To můžeme vyjádřit jako n = m/M_m, kde M_m je hmotnost molu vzduchu.

  Pro naši situaci tedy můžeme psát:

  \[p_1V_1 = nRT= \frac{m}{M_m}RT \rightarrow m = \frac{p_1V_1M_m}{RT} = \frac{100{\cdot} 10^3 \text{ Pa}\ \cdot \ 10{\cdot} 10^{-6} \text{ m}^3 \ \cdot \ 29{\cdot} 10^{-3} \text{ kg}\cdot \text{mol}^{-1}}{8{,}31 \text{ J}\cdot \text{mol}^{-1}\cdot \text{ K}^{-1} \ \cdot \ 293{,}15 \text{ K}} \, \dot =\, 1{,}2{\cdot} 10^{-5} \text{ kg}\]

• Nápověda b) Izotermická expanze

  Známe objem V₁ a tlak p₁ na začátku děje a objem V₂ na konci děje. Vzpomeňte si na vztah popisující izotermický děj, který vám umožní vypočítat tlak p₂.

  Uvědomte si, na které stavové veličině závisí vnitřní energie ideálního plynu, a o jaký děj se v našem případě jedná. Co na základě toho můžete říci o změně vnitřní energie vzduchu ve stříkačce?

• Řešení nápovědy b) Izotermická expanze

  Pro izotermický děj platí:

  \[p_1V_1 = p_2V_2 \rightarrow p_2 = \frac{p_1V_1}{V_2} = \frac{100{\cdot} 10^3 \ \text{Pa} \ \cdot \ 10 \ \text{cm}^{3}}{12{,}5 \ \text{cm}^{3}} = 80 \ \text{kPa}\]

  Vnitřní energie je jen funkcí teploty. Ta se při izotermickém ději nemění a stejně tak se nemění vnitřní energie vzduchu ve stříkačce. Změna vnitřní energie je tedy nulová.

  \[\Delta U = 0\]

• Nápověda c) pV diagram

  Znáte tlak a objem vzduchu na začátku i na konci děje, a tedy i souřadnice 2 bodů v pV diagramu. Jaká křivka je spojuje? Vyjděte ze stavové rovnice.

• Řešení nápovědy c) pV diagram

  Křivka - izoterma musí procházet body (p₁, V₁) = (100 kPa, 10 cm³) a (p₂, V₂) = (80 kPa, 12,5 cm³).

  Pro izotermický děj platí:

  \[pV = \text{konstanta} \rightarrow p = \frac{\text{konstanta}}{V}\]

  Izoterma je část hyperboly.

  

• Nápověda d) Obsah plochy pod grafem

  Plochu pod křivkou si můžete rozdělit na trojúhelník a obdélník. Jejich obsah již snadno spočítáte.

  Veličinu, kterou plocha pod křivkou reprezentuje, vám může pomoci určit i jednotka, v jaké obsah plochy vyjde.

• Řešení nápovědy d) Obsah plochy

  Pokud aproximujeme část izotermy úsečkou, můžeme plochu rozdělit na obdelník a trojúhelník, obsah plochy bude součtem obsahů těchto dvou útvarů:

  \[S = 2{,}5{\cdot} 10^{-6} \ \text{m}^{3} \ \cdot \ 80{\cdot} 10^3 \ \text{Pa}\ + \ \frac{1}{2}\cdot2{,}5{\cdot} 10^{-6} \ \text{m}^3 \ \cdot \ 20{\cdot} 10^3 \ \text{Pa} = 0{,}225 \ \text{J}\]

  

  Jednotka, ve které obsah plochy vyšel, je joule. Obsah plochy pod grafem reprezentuje celkovou práci vykonanou plynem během izotermické expanze.

• Nápověda e) Vyměněné teplo

  Vyjděte z 1. věty termodynamické a připomeňte si, jaká je změna vnitřní energie během izotermické expanze. Práci vykonanou plynem znáte, takže vyměněné teplo již snadno určíte.

• Řešení nápovědy e) Vyměněné teplo

  První věta termodynamická říká, že teplo, které dodáme plynu, jde na změnu jeho vnitřní energie a práci, kterou plyn vykoná: Q = \(\Delta U\) + W.

  Změna vnitřní energie je při izotermické expanzi rovna nula. Aby plyn vykonal práci W = 0,225 J, tak mu musíme dodat teplo o stejné velikosti.

  \[Q = W = 0{,}225\ \text{J}\]

• Nápověda f) Opakování experimentu

  Plyn zvětšuje svůj objem, koná tedy práci, stěny stříkačky jsou ovšem izolované, plyn si nevyměňuje s okolím teplo (adiabatický děj). Využijte opět 1. větu termodynamickou a určete s její pomocí, co se bude dít s vnitřní energií a teplotou.

  K určení toho, jak se změní tlak, pak využijte stavovou rovnici.

  Pro rozhodnutí, zda a jak se změní hustota, si připomeňte, jak je definovaná a zda se veličiny, které v její definici vystupují, mění.

• Řešení nápovědy f) Opakování experimentu

  Vnitřní energie a teplota:

  1. věta termodynamická:

  \[Q = \Delta U + W \rightarrow 0 = \Delta U + W\]

  Vzduch ve stříkačce koná práci na úkor své vnitřní energie. Ta se tedy snižuje. Vnitřní energie a tím pádem i teplota budou na konci nového (adiabatického) děje nižší než na jeho začátku.

  Vzhledem k tomu, že při izotermickém ději se teplota ani vnitřní energie neměnila, bude vnitřní energie i teplota po změně při adiabatickém ději nižsí než po změně při ději izotermickém.

  Tlak:

  Podle stavové rovnice platí: \[\frac{p_2V_2}{T_2} = \frac{p'_2V'_2}{T'_2},\] nečárkované veličiny popisují stav na začátku adiabatického děje, čárkované na jeho konci.

  Podobně můžeme pro izotermický děj z části b) psát: \[\frac{p_1V_1}{T_1} = \frac{p'_1V'_1}{T'_1},\] nečárkované veličiny popisují stav na začátku izotermického děje, čárkované na jeho konci.

  Nyní porovnáme situace na konci obou dějů. Objem V₂´ je roven objemu V₁´. Vzhledem k tomu, že teplota T₂´ je nižší než teplota T₁´, musí být také tlak p₂´ na konci adiabatického děje nižší než tlak p₁´ na konci izotermického děje.

  Hustota:

  Hustota je definovaná jako: \(\rho = \frac{m}{V}\), kde m je hmotnost a V objem látky. Vzhledem k tomu, že hmotnost vzduchu v stříkačce se nemění a stejný je i jeho objem na konci obou děju, bude stejná i jeho hustota, \(\rho_2 = \rho_1\).

• Odpovědi

  a)	Hmotnost vzduchu ve stříkačce je m = 1,19 10-5 kg.
  b)	Tlak vzduchu ve stříkačce po izotermické změně má hodnotu p2 = 80 kPa. Změna vnitřní energie vzduchu ve stříkačce je nulová, tj. \(\Delta U\) = 0.
  d)	Obsah plochy pod grafem je roven práci vykonané plynem během izotermické expanze, tedy S = W = 0,225 J.
  e)	Teplo, které si vzduch během izotermické expanze vymění s okolím, je rovno Q = 0,225 J.
  f)	Hustota vzduchu bude stejná na konci obou dějů (izotermického i adiabatického), tlak, teplota i vnitřní energie budou menší na konci druhého, adiabatického děje.