Změna rozměrů kovové desky při zahřívání
Úloha číslo: 2052
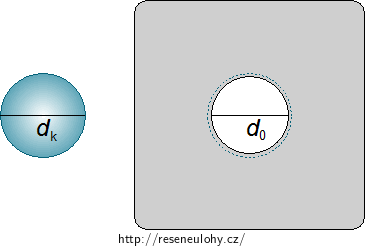
V hliníkové destičce o rozměrech 10 cm x 10 cm je kulatý otvor o průměru 36 mm. O kolik stupňů musíme destičku zahřát, aby otvorem mohla projít kulička, jejíž průměr je 36,1 mm?
Zápis
d0 = 36,0 mm = 3,60·10−2 m průměr kulatého otvoru před zahřátím l0 obvod kulatého otvoru před zahřátím dk = 36,1 mm = 3,61·10−2 m průměr kuličky lk obvod nejmenšího otvoru, kterým kulička projde Z tabulek:
α = 2,4·10−5 K−1 součinitel teplotní délkové roztažnosti hliníku Rozbor
Otvor v destičce je menší než obvod průmětu kuličky do roviny (dále jen obvod kuličky). Zahřejeme-li destičku, její rozměry i otvor uprostřed se zvětší v důsledku teplotní roztažnosti. Kulička tak bude moci otvorem projít.
K řešení úlohy budeme potřebovat znát vztah pro prodloužení předmětu při délkové teplotní roztažnosti. Tento vztah využíváme k výpočtu změn délek předmětů, jejichž jeden rozměr je výrazně větší, než zbylé dva (např. tyče nebo dráty). Můžeme si představit, že kovová destička je tvořena spoustou tenkých kovových pásků. Potom při výpočtu jejího zvětšení zahřátím můžeme využít vztah pro délkovou teplotní roztažnost.
Obr. 1: Obvod kuličky je znázorněn čárkovanou čarou okolo otvoru v destičce.
Obvod otvoru se musí zvětšit, aby minimálně odpovídal obvodu kuličky. Napíšeme tedy vztah pro zvětšený obvod otvoru po zahřátí a položíme ho roven obvodu kuličky. Odtud pak vyjádříme potřebnou změnu teploty.
Nápověda
Představte si destičku "rozkrájenou" na tenké soustředné kroužky se středem uprostřed otvoru. Napište, jak se změní obvod takového kroužku při zahřátí o teplotu Δt.
Řešení
Obvod kulatého otvoru o průměru d0 před zahřátím vypočítáme jako
\[l_{\mathrm{0}} = πd_{\mathrm{0}}.\tag{1}\]Zvýší-li se teplota hliníkové destičky o Δt, zvětší se kulatý otvor a pro jeho obvod l bude platit vztah
\[l = l_{\mathrm{0}}(1+αΔt).\tag{2}\]Kulička má průměr dk. Otvor, kterým by kulička prošla, musí tedy mít průměr alespoň dk. Obvod takového otvoru lk vypočítáme jako
\[l_{\mathrm{k}} = πd_{\mathrm{k}}.\tag{3}\]Aby kulička mohla projít otvorem, musí být jeho obvod po zahřátí alespoň lk. Do vztahu (2) dosadíme za l obvod kuličky lk
\[l_{\mathrm{k}} = l_{\mathrm{0}}(1+αΔt).\]Do vztahu (2) nyní dosadíme (1) a (3)
\[πd_{\mathrm{k}} = πd_{\mathrm{0}}(1+αΔt),\]tento vztah upravíme a vyjádříme z něho Δt
\[\frac{d_{\mathrm{k}}}{d_{\mathrm{0}}}−1 = αΔt\] \[Δt = \frac{d_{\mathrm{k}}−d_{\mathrm{0}}}{α·d_{\mathrm{0}}}.\tag{4}\]Dále do vztahu (4) dosadíme hodnoty ze zadání a vypočítáme, o kolik stupňů je potřeba zahřát destičku
\[Δt = \frac{3{,}61·10^{−2}−3{,}60·10^{−2}}{2{,}4·10^{−5}·3{,}60·10^{−2}} °\mathrm{C}\] \[Δt \dot{=} 115{,}7 °\mathrm{C}.\]Odpověď
Chceme-li, aby kulička prošla kulatým otvorem, je třeba ohřát hliníkovou destičku alespoň o 115,7 °C.
Odkaz na pokus
Pokus k této úloze najdete zde: Zahřívání hliníkové desky s otvorem.




