První termodynamický zákon

Úloha číslo: 4507

V nádobě s objemem 280 cm³ je plyn hélium (He) s počáteční teplotou 306 K a tlakem p₀ = 10⁵ Pa.

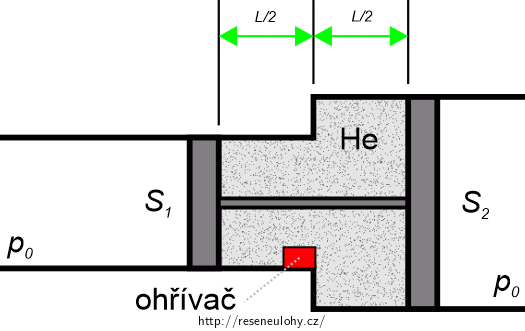
Nádoba s héliem zůstává ve dvou spojených potrubích s průřezem S₁ = 30 cm² a S₂ = 40 cm², které jsou uzavřené písty spojenými tuhou tyčí délky l = 8,0 cm (viz náčrtek). Písty jsou ve stejné vzdálenosti od spoje potrubí. Na vnější straně pístů je vzduch s konstantním tlakem p₀ = 10⁵ Pa. Potrubí i píst jsou dobře tepelně izolované. Písty se mohou pohybovat bez tření, stále dobře těsní.

V blízkosti spoje potrubí je instalovaný ohřívač, kterým se hélium ohřeje na teplotu 339 K. Při ohřívání se píst posune o 3,0 cm doprava, aby se tlak hélia opět vyrovnal s vnějším tlakem vzduchu p₀.

a)	Vypočítejte látkové množství hélia v nádobě.
b)	Vypočítejte počet atomů hélia v nádobě.
c)	Vypočítejte změnu vnitřní energie hélia. Molární tepelná kapacita hélia při stálém objemu je \(c_V = \frac{3}{2}R\).
d)	Vypočítejte objem hélia po zahřátí.
e)	Vypočítejte práci, kterou vykoná hélium při pohybu pístů.
f)	Vypočítejte výkon ohřívače, pokud byl zapnutý po dobu 25 s.

Zápis

V₁ = 280 cm³	objem nádoby s héliem
T = 306 K	původní teplota hélia v nádobě
S₁ = 30 cm²	průřez prvního potrubí
S₂ = 40 cm²	průřez druhého potrubí
l = 8 cm	délka tyče
T₁ = 339 K	teplota hélia po zahřívání
\(\Delta x\) = 3,0 cm	posunutí pístu doprava
t = 25 s	čas, po který byl ohřívač zapnut

a) n = ?	látkové množství hélia v nádobě
b) N = ?	počet atomů hélia v nádobě
c) \(\Delta U\) = ?	změna vnitřní energie hélia
d) V₂ = ?	objem hélia po zahřátí
e) W = ?	práce vykonána héliem při pohybu pístů
f) P = ?	výkon ohřívače

p₀ = 10⁵ Pa	atmosférický tlak
R = 8,314 J·mol^-1·K^-1	molární plynová konstanta
N_A = 6,022·10²³ mol^-1	avogadrova konstanta
c_V = \(\frac{3}{2}R\)	molární tepelná kapacita hélia

Nápověda a: látkové množství
Známe tlak, objem a teplotu hélia v nádobě, pomocí jaké rovnice můžeme dopočítat látkové množství n?
Řešení nápovědy a: látkové množství
Látkové množství n můžeme dopočítat pomocí stavové rovnice ideálního plynu, platí tedy
\[p_0V_1 = nRT \rightarrow n = \frac{p_0V}{RT} = \frac{10^5 \ \text{Pa} \ \cdot \ 280 {\cdot} 10^{-6} \ \text{m}^{3}}{8{,}31 \ \text{J}\cdot \text{mol}^{-1}\cdot\text{K}^{-1} \ \cdot \ 306 \ \text{K}} \, \dot =\, 1{,}1{\cdot} 10^{-2} \ \text{mol.}\]
Nápověda b: počet atomů
Známe látkové množství n hélia v nádobě. Kolik částic obsahuje 1 mol látky, která konstanta to udává?
Řešení nápovědy b: počet atomů
Jeden mol libovolné látky obsahuje 6,02·10²³ částic, což je hodnota Avogadrovy konstanty N_A vyjádřené v mol^-1. Počet atomů hélia v nádobě tedy bude:
\[N = nN_A = \frac{10^5 \ \text{Pa} \ \cdot \ 280 {\cdot} 10^{-6} \ \text{m}^{3} \ \cdot \ 6{,}02{\cdot} 10^{23} \ \text{mol}^{-1}}{8{,}31 \ \text{J}\cdot \text{mol}^{-1}\cdot\text{K}^{-1} \ \cdot \ 306 \ \text{K}} \, \dot =\, 6{,}63{\cdot} 10^{21}.\]
Nápověda c: změna vnitřní energie plynu
Při ohřívání se vnitřní energie plynu samozřejmě zvětšuje, množství plynu v nádobě zůstává konstantní, jak můžeme pomocí počáteční a koncové teploty spočítat změnu energie plynu? Známe molární tepelnou kapacitu hélia při stálém objemu (viz zápis).
Řešení nápovědy c: změna vnitřní energie plynu
Pro změnu vnitřní energie platí vztah:
\[\Delta U = nc_V(T_1 - T) = \frac{3}{2}\cdot 8{,}31 \ \text{J}\cdot \text{mol}^{-1}\cdot\text{K}^{-1} \ \cdot \ 1{,}1{\cdot}10^{-2} \ \text{mol}\ \cdot \ (339 \ \text{K} - 306 \ \text{K}) \, \dot =\, 4{,}5 \ \text{J.}\]
Nápověda d: objem hélia po zahřátí
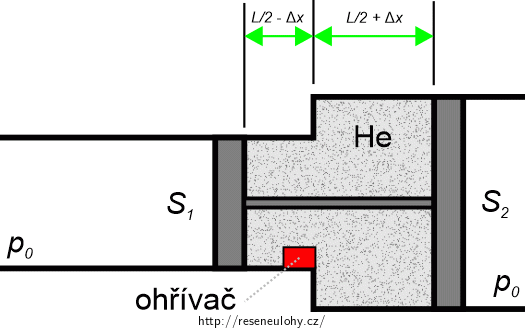
Nakreslete si situaci po posunutí pístu a vyjádřete objemy obou částí potrubí. Uvažujeme, že tyč se nijak nezkracuje ani neprodlužuje, pouze se posune doprava o \(\Delta x = 3{,}0 \ \text{cm.}\)
Řešení nápovědy d: objem hélia po zahřátí
Objem plynu můžeme vypočítat jako součet objemu hélia v menším potrubí a objemu hélia ve větším potrubí. Situaci znázorňuje náčrtek.
\[V_2 = S_1 \left(\frac{L}{2} - \Delta x \right) + S_2 \left(\frac{L}{2}- \Delta x \right) = 3{\cdot} 10^{-3} \ \text{m}^2 \ \cdot \ (4{,}0{\cdot} 10^{-2} \ \text{cm}- 3{,}0{\cdot} 10^{-2} \ \text{cm}) \ + \] \[ \ + 3{\cdot} 10^{-3} \ \text{m}^2 \ \cdot \ (4{,}0{\cdot} 10^{-2} \ \text{cm} + 3{,}0{\cdot} 10^{-2} \ \text{cm}) = 3{\cdot} 10^{-3} \ \text{m}^2 \ \cdot \ 10^{-2} \ \text{m} + 4{\cdot} 10^{-3} \ \text{m}^{2} \ \cdot \ 7{\cdot}10^{-2} \ \text{m}\] \[= \ 31{\cdot}10^{-5} \ \text{m}^{3} = 310 \ \text{cm}^{3}.\]
Nápověda e: práce vykonaná plynem
Známe objem hélia na začátku a na konci děje. Víme, že tlak plynu je během ohřívání a posouvání pístu konstantní. Jak z toho můžeme vypočítat práci vykonanou plynem?
Řešení nápovědy e: práce vykonaná plynem
Práci vykonanou plynem můžeme vypočítat následovně:
\[ W = p\Delta V = p_0(V_2 - V_1) = 10^{5} \ \text{Pa} \ \cdot \ (31 - 28) \cdot 10^{-5} \ \text{m}^3 = 3 \ \text{J}\]
Nápověda f: výkon ohřívače
Jak je definován výkon pomocí energie a času? Jakou celkovou energii dodal ohřívač soustavě?
Řešení nápovědy f: výkon ohřívače
Ohřívač dodal soustavě energii ve formě tepla Q, které se spotřebovalo na
1. ohřátí plynu o \(\Delta T\) a změnu jeho vnitřní energie, přičemž \(\Delta U \, \dot =\, 4{,}5 \ \text{J,}\)
2. práci W = 3 J, kterou plyn vykonal při pohybu pístů.
Výkon ohřívače P je tedy:
\[P = \frac{Q}{t} = \frac{4{,}5 \ \text{J} + 3 \ \text{J}}{25 \ \text{s}} = 0{,}3 \ \text{W.}\]

Odpovědi

a)	Látkové množství hélia v nádobě je n \(\dot{=}\) 1,1·10^-2 mol.
b)	Počet atomů hélia v nádobě je N \(\dot{=}\) 6,63·10²¹.
c)	Změna vnitřní energie hélia je \(\Delta U \, \dot =\, 4{,}5 \ \text{J.}\)
d)	Objem hélia po zahřátí je V₂ = 310 cm³.
e)	Práce, kterou hélium vykoná při pohybu pístů je W = 3 J.
f)	Výkon ohřívače je P = 0,3 W.