Práce, teplo a změna vnitřní energie kyslíku
Úloha číslo: 424
Počáteční objem kyslíku je 5 l a jeho tlak 100 kPa. Nejdříve jej izobaricky zahřejeme na dvojnásobný objem a následně izochoricky zvýšíme jeho tlak na čtyřnásobek původního tlaku. Určete, jakou práci plyn vykonal, jaké teplo jsme mu dodali a jak se změnila jeho vnitřní energie.
Zápis
V1 = 5 l = 0,005 m3 počáteční objem kyslíku p1 = 100 kPa = 105 Pa počáteční tlak kyslíku V2 = 2V1 objem po zahřátí p3 = 4p1 izochoricky zvýšený tlak W = ? vykonaná práce Q = ? dodané teplo ΔU = ? změna vnitřní energie p–V diagram
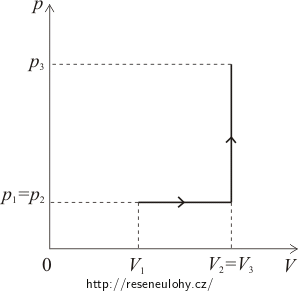
Nápověda 1 – výpočet tepla
Pro výpočet tepla dodaného při izobarickém ději použijte vztah mezi teplem Q a molární tepelnou kapacitou Cp za stálého tlaku
\[Q=nC_p\mathrm{\Delta}T,\]kde n je látkové množství a ΔT je změna teploty plynu.
Pro výpočet tepla dodaného při izochorickém ději použijte analogický vztah mezi teplem Q a molární tepelnou kapacitou CV za stálého objemu
\[Q=nC_V\mathrm{\Delta}T,\]kde n je látkové množství a ΔT je změna teploty plynu.
Nápověda 2 – molární tepelná kapacita kyslíku
Molární tepelná kapacita kyslíku při stálém tlaku je
\[C_p=\frac{7}{2}R.\]Molární tepelná kapacita kyslíku při stálém objemu je
\[C_V=\frac{5}{2}R.\]Nápověda 3 – vyjádření změny teploty
Pro vyjádření změny teploty při izobarickém ději použijte tzv. Gay-Lussacův zákon a při izochorickém ději tzv. Charlesův zákon.
Rozbor – dodané teplo
Celkové dodané teplo je rovno součtu tepla dodaného při izobarickém a tepla dodaného při izochorickém ději.
Teplo dodané při izobarickém ději vyjádříme jako součin látkového množství, molární tepelné kapacity při stálém tlaku a změny teploty v průběhu děje. Změnu teploty určíme pomocí tzv. Gay-Lussacova zákona. Nakonec využijeme stavovou rovnici ideálního plynu, abychom mohli teplo vyjádřit pouze pomocí zadaných veličin.
Analogicky budeme postupovat i při výpočtu tepla dodaného při izochorickém ději. V jeho vyjádření však použijeme molární tepelnou kapacitu při stálém objemu a změnu teploty určíme pomocí tzv. Charlesova zákona.
Výpočet dodaného tepla
Protože teplo dodáváme plynu při obou procesech, platí pro celkové dodané teplo Q vztah
\[Q=Q_1+Q_2,\]kde Q1 a Q2 jsou po řadě dodaná tepla při izobarickém a izochorickém ději.
K výpočtu tepla Q1 dodaného při izobarickém ději použijeme vztah mezi teplem a molární tepelnou kapacitou Cp za stálého tlaku
\[Q_1=nC_p\left(T_2-T_1\right),\]kde n je látkové množství, T2 a T1 jsou koncová a počáteční teplota plynu.
S uvážením faktu, že kyslík je dvouatomový plyn a má tudíž molární tepelnou kapacitu při stálém tlaku
\[C_p=\frac{7}{2}R\]můžeme psát
\[Q_1=\frac{7}{2}nR\left(T_2-T_1\right).\]Podle Gay-Lussacova zákona platí, že zvýší-li se objem izobaricky na dvojnásobek, zvýší se na dvojnásobek i teplota, tedy T2 = 2T1. Po dosazení do předchozího vztahu dostaneme
\[Q_1=\frac{7}{2}nR\left(2T_1-T_1\right)=\frac{7}{2}nRT_1.\]Nyní využijeme stavovou rovnici ideálního plynu
\[p_1V_1=nRT_1 \qquad\Rightarrow\qquad nT_1=\frac{p_1V_1}{R}.\]Dosazením získáme vztah
\[Q_1=\frac{7}{2}R\frac{p_1V_1}{R}=\frac{7}{2}p_1V_1.\]Pro teplo Q2 dodané při izochorickém ději platí vztah
\[Q_2=nC_V\left(T_3-T_2\right).\]Molární tepelná kapacita při stálém objemu je pro kyslík
\[C_V=\frac{5}{2}R\]a tedy můžeme psát
\[Q_2=\frac{5}{2}nR\left(T_3-T_2\right).\]Podle Charlesova zákona pro izochorický děj platí: zvýší-li se tlak na čtyřnásobek, zvýší se čtyřnásobně i teplota, tudíž T3 = 4T2 = 8T1.
Po dosazení do předchozího vztahu
\[Q_2=\frac{5}{2}nR\left(8T_1-2T_1\right)=15nRT_1\]a opětovném použití stavové rovnice ideálního plynu
\[nT_1=\frac{p_1V_1}{R}\]dostaneme pro teplo Q2 vztah
\[Q_2=15R\frac{p_1V_1}{R}=15p_1V_1.\]Celkové dodané teplo Q je potom
\[Q=Q_1+Q_2=\frac{7}{2}p_1V_1+15p_1V_1,\] \[Q=\frac{37}{2}p_1V_1.\]Nápověda 4 – výpočet práce
Práce vykonaná plynem je nenulová při izobarickém zahřátí a platí pro ni vztah
\[W=p\left(V_2-V_1\right),\]kde p je tlak plynu, V1 a V2 jsou objemy plynu před a po zahřátí.
Při izochorickém ději je objem plynu konstantní, proto plyn práci nekoná.
Nápověda 5 – změna vnitřní energie
K výpočtu změny vnitřní energie ΔU použijte 1. termodynamický zákon.
Rozbor – vykonaná práce a změna vnitřní energie
Především si musíme uvědomit, že plyn koná práci jen při izobarickém zahřátí. Tuto práci vyjádříme jako součin tlaku a změny objemu plynu v průběhu děje.
Změnu vnitřní energie určíme z 1. termodynamického zákona.
Výpočet vykonané práce a změny vnitřní energie
Práce W vykonaná plynem je nenulová pouze při izobarickém zahřátí a platí pro ni vztah
\[W=p_1\left(V_2-V_1\right),\]kde p1 je tlak plynu, V1 a V2 jsou objemy plynu před a po zahřátí.
Po dosazení za objem V2
\[W=p_1\left(2V_1-V_1\right)\]ihned dostaneme
\[W=p_1V_1.\]Změnu vnitřní energie ΔU určíme z 1. termodynamického zákona jako rozdíl dodaného tepla Q a vykonané práce W
\[\Delta U=Q-W=\frac{37}{2}p_1V_1 -p_1V_1= \frac{35}{2}p_1V_1.\]Číselné dosazení
\[Q=\frac{37}{2}p_1V_1=\frac{37}{2}\cdot{0{,}005}\cdot{10^5}\,\mathrm{J}=9250\,\mathrm{J}=9{,}25\,\mathrm{kJ}\] \[W=p_1V_1=0{,}005\cdot{10^5}\,\mathrm{J}=500\,\mathrm{J}\] \[\Delta U=Q-W=\left(9250-500\right)\,\mathrm{J}=8750\,\mathrm{J}=8{,}75\,\mathrm{kJ}\]Odpověď
Plyn vykonal práci 500 J, bylo mu dodano teplo 9,25 kJ a přírůstek jeho vnitřní energie byl 8,75 kJ.



