Korková loďka
Úloha číslo: 342
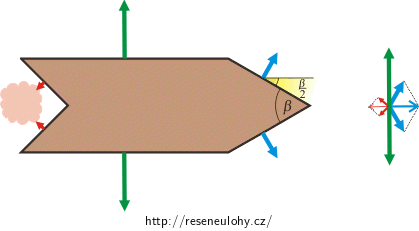
Na hladině vody plave korková lodička o hmotnosti 50 g, která má tvar podle obrázku. Do místa A kápneme malé množství mycího prostředku. Povrchové napětí směsi vody a mycího prostředku za loďkou má čtvrtinovou hodnotu v porovnání s čistou vodou.
a) Vysvětlete, co se stane s loďkou a proč.
b) Jak velká síla působí na loďku a s jak velkým zrychlením by se loďka pohybovala, pokud bychom zanedbali odporovou sílu vody?
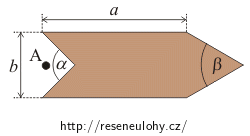
Uvažujte následující rozměry loďky:
a = 20 cm, b = 5 cm, α = 90° a β = 60°.
Nápověda
Díky povrchovému napětí působí voda okraje loďky povrchovou silou. Tato síla míří vodorovně a kolmo na loďku. Její velikost je úměrná povrchovému napětí a délce okraje loďky.
Nakreslete si síly, které působí na jednotlivé hrany loďky, a rozmyslete si, kam bude mířit jejich výslednice.
Zápis
a = 20 cm, b = 5 cm, α = 90°, β = 60° rozměry loďky m = 50 g = 0,05 kg hmotnost loďky σm = σv vztah mezi povrch. napětími vody s mycím prostředkem a čisté vody Z tabulek: σv = 73 mN m-1 povrchové napětí čisté vody Rozbor a řešení části a)
Díky povrchovému napětí působí povrch kapaliny na svém okraji na nádobu nebo předmět, který z kapaliny vyčnívá, povrchovou silou. Tato síla je vždy kolmá k okraji hladiny. Můžeme si to také představit tak, že se kapalina snaží „zmenšit svůj povrch“. Působící síla je úměrná povrchovému napětí (konstantně charakterizující kapalinu) a délce, na které působí.
Ve svislém směru na loďku působí tíhová síla a vztlaková síla. Protože loďka plave na hladině, jsou tyto dvě síly stejně velké a opačného směru. Ve vodorovném směru působí na loďku povrch vody (viz obrázek) povrchovými silami.
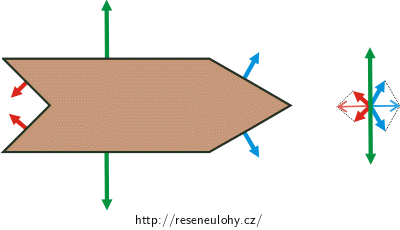
Jestliže je kolem loďky ze všech stran voda, je výslednice všech těchto sil nulová a loďka je tedy v klidu. Detailně bude tento výsledek vidět při početním řešení úlohy.
Kápneme-li za loďku mycí prostředek, zmenšíme povrchové napětí za loďkou, a tedy zmenšíme i síly, které působí na zadní část loďky. Díky tomu budou síly působící na předek loďky větší a uvedou loďku do pohybu směrem vpřed. Do obrázku si tedy zakreslíme síly, kterými povrch vody na loďku působí, určíme jejich výslednici a díky znalosti hmotnosti loďky můžeme spočítat i zrychlení, které by tato síla loďce udělila.
Řešení části b)
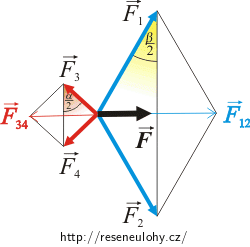
Z obrázků uvedených v rozboru je patrné, že pro výpočet výsledné povrchové síly, která bude působit na loďku, jsou důležité povrchové síly působící na „šikmé části loďky“. Nakreslíme si je do detailního obrázku a vyznačíme známé síly.
Výslednici „modrých“ sil \(\vec{F}_1\) a \(\vec{F}_2\) působících na přední část loďky si označíme \(\vec{F}_{12}\). A podobně výslednici „červených“ \(\vec{F}_3\) a \(\vec{F}_4\) působících na zadní část loďky si označíme \(\vec{F}_{34}\).
Našim úkolem je spočítat výslednici těchto sil, tj. velikost síly F:
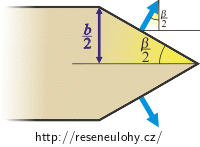
\[\vec{F}\,=\,\vec{F}_1\,+\vec{F}_2\,+\vec{F}_3\,+\,\vec{F}_4\,=\,\vec{F}_{12}\,+\,\vec{F}_{34}.\]Síly \(\vec{F}_1\) a \(\vec{F}_2\) působí na stranu loďky o délce: \[\frac{\frac{b}{2}}{\cos \frac{\beta}{2}}\,.\] Pro jejich velikost tedy platí:
\[F_1\,=\,F_2\,=\, \sigma_\mathrm{v} \, \frac{b}{ 2 \cos \frac{\beta}{2}},\] \[F_{12}\,=\, 2F_1 \,\cos \frac{\beta}{2} \,=\, 2\sigma_\mathrm{v} \, \frac{b}{ 2 \cos \frac{\beta}{2}}\,\cos \frac{\beta}{2}\,=\, 2\sigma_\mathrm{v} b.\]Podobně vyjádříme velikosti sil \(\vec{F}_3\) a \(\vec{F}_4\) i jejich výslednice \(\vec{F}_{34}\) . Nesmíme ale zapomenout, že kromě jiného úhlu musíme také dosadit jiné povrchové napětí, protože za loďkou je mýdlový roztok:
\[F_3\,=\,F_4\,=\, \sigma_\mathrm{m} \, \frac{b}{ 2 \cos \frac{\alpha}{2}},\] \[F_{34}\,=\, 2F_3 \,\cos \frac{\alpha}{2} \,=\, 2\sigma_\mathrm{m} \, \frac{b}{ 2 \cos \frac{\alpha}{2}}\,\cos \frac{\alpha}{2}\,=\, 2\sigma_\mathrm{m} b.\]Síly \(\vec{F}_{12}\) a \(\vec{F}_{34}\) působí v opačných směrech, proto je velikost jejich výslednice dána rozdílem jejich velikostí:
\[F \,=\, F_{12}\,-\, F_{34}\, =\, \sigma_\mathrm{v} b \,-\, \sigma_\mathrm{m} b \,=\, (\sigma_\mathrm{v} - \sigma_\mathrm{m} ) b. \]Z tohoto vztahu je také jasně patrné, že před kápnutím mycího prostředku (tedy ve chvíli, kdy povrchové napětí před i za loďkou je stejné) je výslednice působících sil nulová a loďka tedy zůstává v klidu.
Dosaďme zadané hodnoty:
\[F \,=\, (\sigma_\mathrm{v} - \frac{1}{4}\sigma_\mathrm{v} ) b\,=\, \frac{3}{4}\sigma_\mathrm{v} b \,=\, \frac{3}{4}\,\cdot \, 0{,}073 \,\cdot\, 0{,}05 \, \mathrm{N},\] \[F \,\dot=\, 2{,}7\, \mathrm{mN}.\]Velikost zrychlení, které by loďce udělila tato síla, určíme z 2. Newtonova zákona:
\[a \,=\, \frac{F}{m}\,=\,\frac{3 \sigma_\mathrm{v} b}{4m}\,=\,\frac{3\,\cdot\,0{,}073\,\cdot\,0{,}05}{4\,\cdot \,0{,}05}\, \mathrm{m\,s}^{-2},\] \[a \,\dot=\, 0{,}05\,\mathrm{m\,s}^{-2}.\]Odpověď
Po kápnutí mycího prostředku za loďku na ni bude působit směrem dopředu síla o velikosti asi 2,7 mN a loďka se dá do pohybu. Pokud by nepůsobila odporová síla vody, udělila by tato síla loďce zrychlení 0,05 m s-2. Ve skutečnosti je ale odporová síla nezanedbatelná a zrychlení loďky by tedy bylo výrazně menší.