Zmizelé reflexe chloridu draselného
Úloha číslo: 2281
Chlorid draselný (KCl) a bromid draselný (KBr) jsou krystaliké látky se stejnou strukturou jako chlorid sodný (NaCl). Reflexe od následujících rovin jsou pozorovány v jejich difraktogramech:
| KBr | \((111)\) | \((200)\) | \((220)\) | \((311)\) | \((222)\) | \((400)\) | \((331)\) |
| KCl | \((200)\) | \((220)\) | \((222)\) | \((400)\) |
a) Proč v difraktogramu KCl chybí některé reflexe, které by měly být povoleny?
b) Bude v difraktogramu KCl pozorována reflexe od roviny \((420)\)?
Nápověda č. 1
Intenzita píku pro danou reflexi \((hkl)\) v difaktogramu je přímo úměrná druhé mocnině velikosti strukturního faktoru \(S_{(hkl)}\):
\[I_{(hkl)} \propto \vert S_{(hkl)} \vert ^2.\]Strukturní faktor \(S_{(hkl)}\) lze spočítat ze vztahu
\[S_{(hkl)}=\sum_{j}f_j \mathrm{e}^{2\pi i (hx_j + ky_j + lz_j)},\]kde index \(j\) čísluje jednotlivé atomy, \(f_j\) je atomový rozptylový faktor \(j\)-tého atomu, a \(x_j, y_j, z_j\) jsou polohy \(j\)-tého atomu v buňce v jednotkách mřížového parametru.
Klíčem k vyřešení úlohy bude zapsat si nejprve strukturní faktory pro obě látky.
Nápověda č. 2
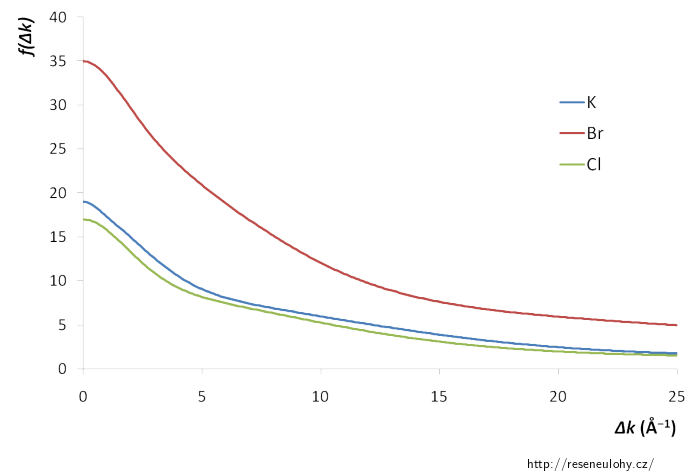
Vyhledejte v literatuře nebo na internetu atomové rozptylové faktory draslíku, bromu a chloru a porovnejte je.
Řešení: Výpočet strukturního faktoru KBr
Nejprve si vypočteme strukturní faktor KBr.
Budeme uvažovat, že atomy draslíku jsou umístěny v polohách
\[x_1=y_1=z_1=0,\] \[x_2=y_2= \frac{1}{2}, z_2=0,\] \[x_3=z_3= \frac{1}{2}, y_3=0,\] \[x_4=0, y_4=z_4= \frac{1}{2}.\]Příspěvek ke strukturnímu faktoru od atomů draslíku tedy bude mít tvar
\[S_{(hkl)}^{\mathrm{K}}=f_{\mathrm{K}}(\mathrm{e}^{2\pi i (h\cdot 0 + k\cdot 0 + l \cdot 0)}+ \mathrm{e}^{2\pi i \frac{1}{2} (h\cdot 1 + k\cdot 1 + l \cdot 0)}+ \mathrm{e}^{2\pi i \frac{1}{2} (h\cdot 1 + k\cdot 0 + l \cdot 1)}+ \mathrm{e}^{2\pi i \frac{1}{2} (h\cdot 0 + k\cdot 1 + l \cdot 1)}). \]Po úpravě
\[S_{(hkl)}^{\mathrm{K}}=f_{\mathrm{K}}(1+\mathrm{e}^{\pi i (h + k)}+\mathrm{e}^{\pi i (h + l)}+\mathrm{e}^{\pi i (k + l)}).\]Stejně budeme postupovat při výpočtu strukturního faktoru atomů bromu, které se nacházejí v pozicích
\[x_1=y_1=y_1=\frac{1}{2},\] \[x_2=y_2= 0, z_2=\frac{1}{2},\] \[x_3=z_3= 0, y_3=\frac{1}{2},\] \[x_4=\frac{1}{2}, y_4=z_4= 0.\]Ke strukturnímu faktoru tedy přispívají členy
\[S_{(hkl)}^{\mathrm{Br}}=f_{\mathrm{Br}}(\mathrm{e}^{2\pi i \frac{1}{2} (h\cdot 1 + k\cdot 1 + l \cdot 1)}+ \mathrm{e}^{2\pi i \frac{1}{2} (h\cdot 0 + k\cdot 0 + l \cdot 1)}+ \mathrm{e}^{2\pi i \frac{1}{2} (h\cdot 0 + k\cdot 1 + l \cdot 0)}+ \mathrm{e}^{2\pi i \frac{1}{2} (h\cdot 1 + k\cdot 0 + l \cdot 0)}), \]neboli
\[S_{(hkl)}^{\mathrm{Br}}=f_{\mathrm{Br}}(\mathrm{e}^{\pi i (h+ k + l )}+ \mathrm{e}^{\pi i l}+\mathrm{e}^{\pi i k}+ \mathrm{e}^{\pi i h}). \]Výsledný strukturní faktor je dán součtem obou příspěvků:
\[S_{(hkl)}^{\mathrm{KBr}}=S_{(hkl)}^{\mathrm{K}}+S_{(hkl)}^{\mathrm{Br}}=f_{\mathrm{K}}(1+\mathrm{e}^{\pi i (h + k)}+\mathrm{e}^{\pi i (h + l)}+\mathrm{e}^{\pi i (k + l)}) + f_{\mathrm{Br}}(\mathrm{e}^{\pi i (h+ k + l )}+ \mathrm{e}^{\pi i l}+\mathrm{e}^{\pi i k}+ \mathrm{e}^{\pi i h}).\]Řešení: Výpočet strukturního faktoru KCl
Dále zapíšeme strukturní faktor KCl. Protože má stejnou mřížku jako KBr a pozice atomů Cl jsou stejné jako pozice atomů Br, stačí vzít výsledky odvozené v předchozí části a nahradit u atomových rozptylových faktorů index Br indexem Cl:
\[S_{(hkl)}^{\mathrm{KCl}}=S_{(hkl)}^{\mathrm{K}}+S_{(hkl)}^{\mathrm{Cl}}=f_K(1+\mathrm{e}^{\pi i (h + k)}+\mathrm{e}^{\pi i (h + l)}+\mathrm{e}^{\pi i (k + l)}) + f_{\mathrm{Cl}}(\mathrm{e}^{\pi i (h+ k + l )}+ \mathrm{e}^{\pi i l}+\mathrm{e}^{\pi i k}+ \mathrm{e}^{\pi i h}).\]Atomové rozptylové faktory draslíku a bromu jsou různé, avšak atomové rozptylové faktory draslíku a chloru jsou podobné. Pokud tedy prohlásíme, že se tyto rozptylové faktory rovnají, můžeme strukturní faktor KCl přepsat do tvaru
\[S_{(hkl)}^{\mathrm{KCl}}=f(1+\mathrm{e}^{\pi i (h + k)}+\mathrm{e}^{\pi i (h + l)}+\mathrm{e}^{\pi i (k + l)} + \mathrm{e}^{\pi i (h+ k + l )}+ \mathrm{e}^{\pi i l}+\mathrm{e}^{\pi i k}+ \mathrm{e}^{\pi i h}),\]kde \(f=f_{\mathrm{K}}=f_{\mathrm{Cl}}\).
Řešení: Zmizení reflexí
Vezměme si nyní reflexe, které v difraktogramu KCl „zmizely“ a vypočtěme pro ně strukturní faktor ze vzorce odvozeného v předchozí části:
\[S_{(hkl)}^{\mathrm{KCl}}=f(1+\mathrm{e}^{\pi i (h + k)}+\mathrm{e}^{\pi i (h + l)}+\mathrm{e}^{\pi i (k + l)} + \mathrm{e}^{\pi i (h+ k + l )}+ \mathrm{e}^{\pi i l}+\mathrm{e}^{\pi i k}+ \mathrm{e}^{\pi i h}).\] Jedna taková reflexe je \((111)\). Pokud skutečně dosadíme do výše uvedeného vztahu \(h=1\), \(k=1\) a \(l=1\), získáme: \[ S_{(111)}^{\mathrm{KCl}}=f(1+\mathrm{e}^{\pi i (1 + 1)}+\mathrm{e}^{\pi i (1 + 1)}+\mathrm{e}^{\pi i (1 + 1)} + \mathrm{e}^{\pi i (1+ 1 + 1 )}+ \mathrm{e}^{\pi i \cdot 1}+\mathrm{e}^{\pi i \cdot 1}+ \mathrm{e}^{\pi i \cdot 1})=\\ =f(1+\mathrm{e}^{2 \pi i}+\mathrm{e}^{2\pi i}+\mathrm{e}^{2\pi i} + \mathrm{e}^{3\pi i}+ \mathrm{e}^{\pi i}+\mathrm{e}^{\pi i}+ \mathrm{e}^{\pi i}). \]Nyní využijeme vztahu
\[\mathrm{e}^{\alpha i}=\cos \alpha + i \sin \alpha.\]Sinus nabývá v hodnotách násobků \(\pi\) vždy nulové hodnoty, proto nás zajímají jen hodnoty funkce kosinus. Ta v těchto hodnotách nabývá hodnot \(\pm 1\):
\[ S_{(111)}^{\mathrm{KCl}}=f(1+1+1+1 -1-1-1-1)=0. \] Naproti tomu strukturní faktor KBr nám vyšel \[S_{(hkl)}^{\mathrm{KBr}}=f_{\mathrm{K}}(1+\mathrm{e}^{\pi i (h + k)}+\mathrm{e}^{\pi i (h + l)}+\mathrm{e}^{\pi i (k + l)}) + f_{\mathrm{Br}}(\mathrm{e}^{\pi i (h+ k + l )}+ \mathrm{e}^{\pi i l}+\mathrm{e}^{\pi i k}+ \mathrm{e}^{\pi i h}),\] čili pro rovinu \((111)\) vychází \[S_{(111)}^{\mathrm{KBr}}=f_{\mathrm{K}}(1+\mathrm{e}^{\pi i (1 + 1)}+\mathrm{e}^{\pi i (1 + 1)}+\mathrm{e}^{\pi i (1 + 1)}) + f_{\mathrm{Br}}(\mathrm{e}^{\pi i (1+ 1 + 1 )}+ \mathrm{e}^{\pi i 1}+\mathrm{e}^{\pi i 1}+ \mathrm{e}^{\pi i 1})=\\ =f_{\mathrm{K}}(1+\mathrm{e}^{2\pi i}+\mathrm{e}^{2\pi i}+\mathrm{e}^{2\pi i}) + f_{\mathrm{Br}}(\mathrm{e}^{3\pi i}+ \mathrm{e}^{\pi i}+\mathrm{e}^{\pi i}+ \mathrm{e}^{\pi i})=\\ =f_{\mathrm{K}}(1+1+1+1)+f_{\mathrm{Br}}(-1-1-1-1)=4f_{\mathrm{K}}-4f_{\mathrm{Br}}\neq 0, \]pokud \(f_{\mathrm{K}} \neq f_{\mathrm{Br}}\).
Řešení: Reflexe (420)
Zajímá nás, jestli se v difraktogramu KCl objeví reflexe \((420)\). To můžeme zjistit, pokud pro tuto reflexi spočítáme strukturní faktor. Pokud bude nulový, daná reflexe se v difraktogramu neobjeví.
V předchozích částech jsme odvodili strukturní faktor KCl
\[S_{(hkl)}^{\mathrm{KCl}}=f(1+\mathrm{e}^{\pi i (h + k)}+\mathrm{e}^{\pi i (h + l)}+\mathrm{e}^{\pi i (k + l)} + \mathrm{e}^{\pi i (h+ k + l )}+ \mathrm{e}^{\pi i l}+\mathrm{e}^{\pi i k}+ \mathrm{e}^{\pi i h}).\]Do něho dosadíme za \(h=4\), \(k=2\) a \(l=0\):
\[S_{(420)}^{\mathrm{KCl}}=f(1+\mathrm{e}^{\pi i (4 + 2)}+\mathrm{e}^{\pi i (4 + 0)}+\mathrm{e}^{\pi i (2 + 0)} + \mathrm{e}^{\pi i (4+ 2 + 0 )}+ \mathrm{e}^{\pi i 0}+\mathrm{e}^{\pi i 2}+ \mathrm{e}^{\pi i 4})=\\ f(1+\mathrm{e}^{6\pi i}+\mathrm{e}^{4\pi i}+\mathrm{e}^{2\pi i} + \mathrm{e}^{6\pi i}+ 1+\mathrm{e}^{2\pi i}+ \mathrm{e}^{4\pi i})=f(1+1+1+1+1+1+1+1)=8f. \]Pík příslušející reflexi od roviny \((420)\) se tedy v difraktogramu objeví.
Strukturní faktor pro K, Br a Cl
Závislost atomového rozptylového faktoru pro K, Br a Cl na rozptylovém vektoru \(\Delta k\) je vykreslena v grafu na následujícím obrázku. Je v něm vidět, že skutečně atomové rozptylové faktory K a Cl si jsou podobné.
