Plovoucí padesátník
Úloha číslo: 1897
Padesátihaléř, který se u nás dříve používal, má hmotnost 0,9 g, průměr 19 mm a výšku 1,7 mm. Pokud padesátihaléř opatrně položíme na vodní hladinu, plave. Zjistěte, zda povrchová síla udrží padesátihaléř na hladině. Zjistěte také, jak moc se padesátník do vody zanoří. Svůj výpočet si ověřte pokusem.
Zápis
m = 0,9 g = 9·10−4 kg hmotnost mince d = 19 mm = 1,9·10−2 m průměr mince v = 1,7 mm = 1,7·10−3 m výška mince
Z tabulek:
σ = 73·10−3 N m−1 povrchové napětí vody Teorie - Povrchové napětí, povrchová síla
Povrch kapaliny se chová jako tenká pružná blána (viz Molekulární tlak v úloze Skleněné destičky ve vodě). Díky tomu se na hladině kapaliny udrží lehké předměty, např. jehla, vážka nebo malá mince.
Chceme-li přemístit molekulu z vnitřku kapaliny do povrchové vrstvy, musíme vykonat určitou práci. Molekuly v povrchové vrstvě tak mají navíc proti molekulám uvnitř kapaliny určitou potenciální energii, kterou nazýváme povrchová energie. Ta je tím větší, čím větší je povrch kapaliny. V rovnovážném stavu se pak kapalina snaží zaujmout co nejmenší povrch a být ve stavu s minimem potenciální energie.
Natáhneme-li např. mýdlovou blánu do drátěného rámečku s jedním pohyblivým ramenem, má blána tendenci se stáhnout a zaujmout menší povrch. Chceme-li ji udržet napjatou, musíme na rameno působit určitou silou. Síle, kterou tahá za rameno blána, říkáme povrchová síla. Ta je přímo úměrná délce ramene či obecně délce okraje povrchové blány.
Povrchové napětí můžeme určit jako podíl velikosti povrchové síly a délky okraje povrchové blány, na nějž kapalina působí kolmo k povrchu kapaliny
\[σ = \frac{F_{\mathrm{p}}}{l}.\]Rozbor
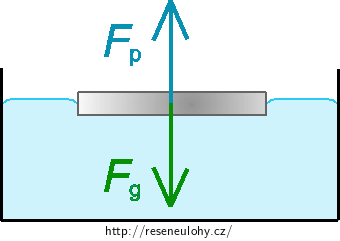
Máme zjistit, jestli povrchová síla udrží padesátihaléř na hladině. To znamená, že musíme zjistit, zda je povrchová síla dostatečně velká, aby kompenzovala tíhovou sílu působící na padesátihaléř. Vypočítáme tedy velikost povrchové síly, velikost tíhové síly a porovnáme jejich velikost. Pokud bude velikost tíhové síly větší než velikost povrchové síly, musí na padesátihaléř působit ještě další síla tak, aby výslednice sil byla nulová.
Nápověda 1 - síly působící na minci
Načrtněte si obrázek a zakreslete do něho síly působící na minci. Dále si napište vztahy, které pro tyto síly platí a vypočítejte jejich velikost.
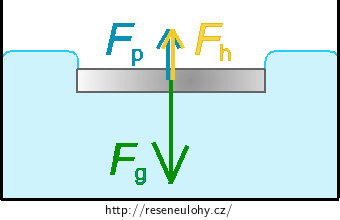
Nápověda 2 - další síla působící na minci
Na těleso ponořené do kapaliny působí tato kapalina hydrostatickou tlakovou silou. Napište vztah, který pro tuto sílu platí.
Nápověda 3 - prohnutí hladiny
Uvědomte si, jaká je výslednice sil působících na minci na hladině. Napište, co pro velikosti sil platí. Odtud pak vyjádříte hloubku zanoření mince.
Číselné dosazení
Nyní už jen dosadíme do vztahu (5) hodnoty známé ze zadání úlohy
\[h = \frac{mg - σπd}{ρgπr^2}\] \[h \dot{=}\, \frac{9·10^{−4}·9{,}8 - 73·10^{−3}·π·1{,}9·10^{−2}}{998·9{,}8·π·(9{,}5·10^{−3})^2} \mathrm{m} \dot{=}\, 1{,}6·10^{−3} \mathrm{m}.\]Odpověď
Zjistili jsme, že povrchová síla není dost velká na to, aby padesátihaléř udržela na hladině. Kromě povrchové síly na minci působí směrem nahoru ještě hydrostatická tlaková síla.
Vypočítali jsme, že hladina vody se pod mincí prohne přibližně o 1,6·10−3 m.
Poznámka: Pokus k této úloze si můžete prohlédnout zde: Padesátník na hladině vody.