Sbírka řešených úloh

Rtuť ve zkumavce

Úloha číslo: 328

Skleněná trubice má koeficient objemové roztažnosti 28,2·10⁻⁶ °C⁻¹. Na jednom konci je zatavena, má všude stejný průřez a při teplotě 0 °C má délku 100 cm. Do této skleněné trubice nalijeme při téže teplotě rtuť s koeficientem objemové roztažnosti 18·10⁻⁵ °C⁻¹ tak vysoko, že rtutí nevyplněný prostor zachovává při změnách teploty stálý objem.

Jak vysoko byla rtuť nalita?

• Nápověda

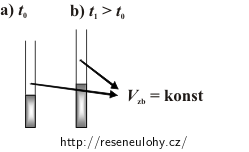
  Rozmyslete si, co se děje s objemem tělesa, které je zahříváno, a jaký vztah musí platit mezi změnami objemů rtuti a trubice, aby se při zahřívání neměnil objem rtutí nevyplněného místa.

• Rozbor

  Při zahřívání trubice se rtutí roste objem rtuti, ale zároveň také trubice. Pokud nechceme, aby se neměnil objem prázdné části trubice během zahřívání, musí být oba přírůstky objemu stejné.

  Požadovanou výšku, do které má být rtuť nalita, tedy získáme z porovnání obou přírůstků objemů, které vyjádříme pomocí tepelné objemové roztažnosti. Dále využijeme skutečnost, že poměr výšky rtuti a výšky trubice je díky neměnícímu se průřezu stejný jako poměr jejich objemů.

• Zápis

  l0 = 100 cm	počáteční délka trubice
  l1 = ?	výška, do které má být nalita rtuť

  Z tabulek:

  β1 = 18·10−5 °C−1	koeficient objemové roztažnosti rtuti
  β2 = 28,2·10−6 °C−1	koeficient objemové roztažnosti skla

• Řešení

  Objem rtuti při původní teplotě si označíme V₁, objem celé trubice V₂. Při zvýšení teploty o Δt se objem rtuti zvětší o hodnotu ΔV₁, pro kterou bude podle základního vztahu pro objemovou roztažnost platit

  \[\mathrm{\Delta} V_{1}=V_{1} \beta_{1}\mathrm{\Delta} t\,,\]

  kde β₁ je koeficient objemové roztažnosti rtuti.

  Stejně tak se však při zahřátí zvětší i objem celé trubice. Pro toto zvětšení bude platit vzorec

  \[\mathrm{\Delta} V_{2}=V_{2} \beta_{2}\mathrm{\Delta} t\,,\]

  kde β₂ je koeficient objemové roztažnosti skla.

  Má-li být objem nevyplněný rtutí nezávislý na teplotě, musí bezpodmínečně platit, že změna objemu rtuti ΔV₁ je stejná jako změna objemu celé trubice ΔV₂.

  S využitím tohoto faktu získáváme:

  \[\mathrm{\Delta} V_{1}=\mathrm{\Delta} V_{2}\,.\]

  Dosadíme z výše uvedených vztahů:

  \[V_{1} \beta_{1}\mathrm{\Delta} t=V_{2} \beta_{2}\mathrm{\Delta} t\,.\]

  Předešlou rovnici upravíme:

  \[\frac{V_{1}}{V_{2}}=\frac{\beta_{2}}{\beta_{1}}\,.\]

  Podíl délek rtuťového sloupce l₁ a celé trubice l₂ je vzhledem ke stejnému obsahu podstavy stejný jako podíl příslušných objemů. Z tohoto důvodu platí pro původní délku rtuťového sloupce vzorec:

  \[\frac{l_{1}}{l_{2}}=\frac{V_{1}}{V_{2}}.\]

  Odsud postupným dosazováním dostaneme:

  \[l_{1}=l_{2}\frac{V_{1}}{V_{2}}=l_{2}\frac{\beta_{2}}{\beta_{1}}\,.\]

• Číselné dosazení

  \[l_{1}=l_{2}\frac{\beta_{2}}{\beta_{1}}=100\cdot \frac{28{,}2\cdot{10^{-6}}}{18\cdot{10^{-5}}}\,\mathrm{cm} \dot{=}16\,\mathrm{cm}\]

• Odpověď

  Rtuť byla nalita do výšky přibližně 16 cm.